- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре по теме Сложение графиков при решении задач с параметрами
Содержание
- 2. Теоретические основы «Сложение графиков» функций При
- 3. Построить графикфункции y=x+sinx
- 4. Теоретические основы Координатно-параметрический методЧтобы решить уравнение координатно-параметрическим
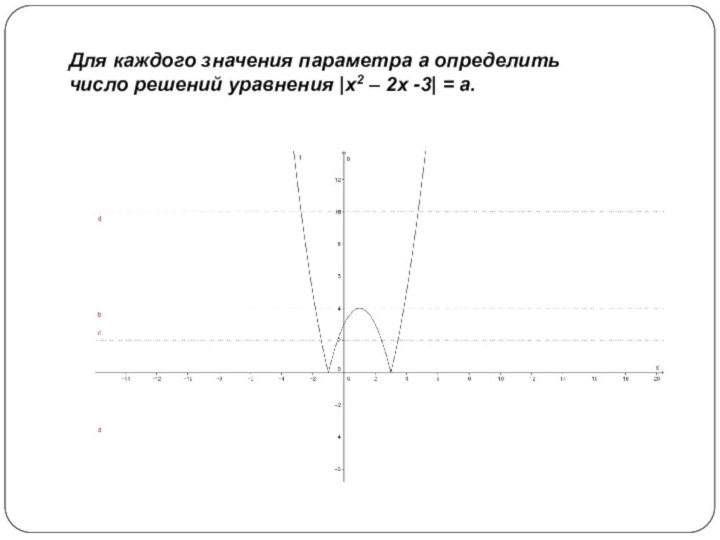
- 5. Для каждого значения параметра a определить число решений уравнения |x2 – 2x -3| = a.
- 6. Формулировка метода Если в задаче фигурирует
- 7. АлгоритмРазбить исходную функцию на «функции-слагаемые»;Найти область определения,
- 8. Ответ: уравнение не имеет корней при a(-2;2)При
- 9. Ответ: при a2 уравнение имеет одно решение,
- 10. Скачать презентацию
- 11. Похожие презентации
Теоретические основы «Сложение графиков» функций При сложении графиков складываются не сами функции y= f (x) и y=g (x), а их значения и каждому значению аргумента x на координатной плоскости ставится в соответствие точка с абсциссой








Слайд 4
Теоретические основы
Координатно-параметрический метод
Чтобы решить уравнение координатно-параметрическим методом, надо:
выразить
параметр а через переменную x
переобозначить координатные оси для работы
в координатно-параметрической плоскости xОaпостроить графический образ уравнения
пересечь полученный график прямыми, перпендикулярными параметрической оси
записать ответ.
Слайд 6
Формулировка метода
Если в задаче фигурирует лишь
один параметр a и одна переменная x и в
плоскости x0a можно построить графики уравнений путём «сложения графиков», то решения находим, пересекая полученный график прямыми, перпендикулярными параметрической оси.
Слайд 7
Алгоритм
Разбить исходную функцию на «функции-слагаемые»;
Найти область определения, граничные
точки области определения и точки разрыва исходной функции;
Исследовать исходную
функцию на чётность (нечётность);Задать плоскость xOa;
Построить графики «функций-слагаемых»;
Определить «разумные» точки;
Построить эскиз графика на основе «сложения графиков»;
Пересечь график прямыми, перпендикулярными параметрической оси;
Записать ответ.
Слайд 8
Ответ: уравнение не имеет корней при a(-2;2)
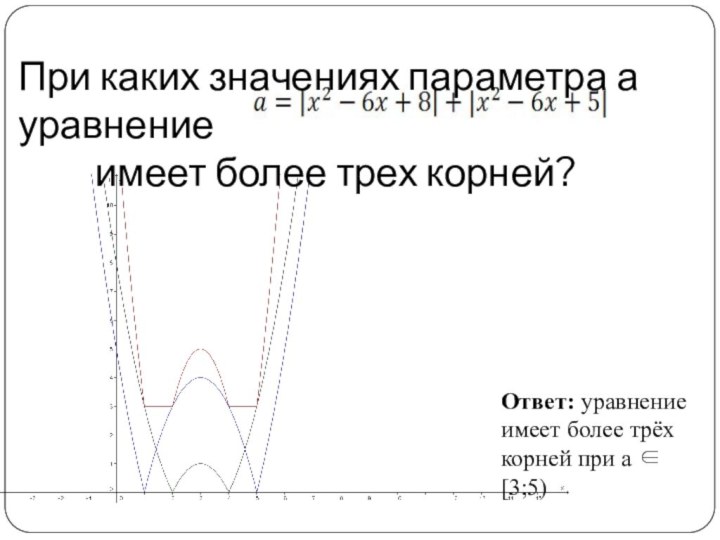
При каких
значениях параметра а уравнение
не имеет корней?
Слайд 9 Ответ: при a2 уравнение имеет одно
решение, при a=2 и a=-2 уравнение имеет два решения,
при -2В зависимости от значений параметра а найти число корней уравнения