Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Решение неравенств с двумя переменными

Содержание

2. ПРОБЛЕМНЫЙ УРОК ИЗУЧЕНИЯ НОВОГО МАТЕРИАЛА. На
3. ПОВТОРИМ ГРАФИКИ ФУНКЦИЙ. У=Х2
4. ВСПОМНИМ РЕШЕНИЕ НЕРАВЕНСТВ Х≤-2
6. Х2 -Х-2 >0
7. ЦЕЛИ УРОКА:Ввести понятие неравенств с двумя переменнымиСоставить алгоритм решения неравенствФормировать навыки решения неравенств
8. ЗАПОМНИТЬРешением неравенства с двумя переменными называется пара
9. Подберем пару чисел, которая будет являться решением
11. А если даны неравенства вида У
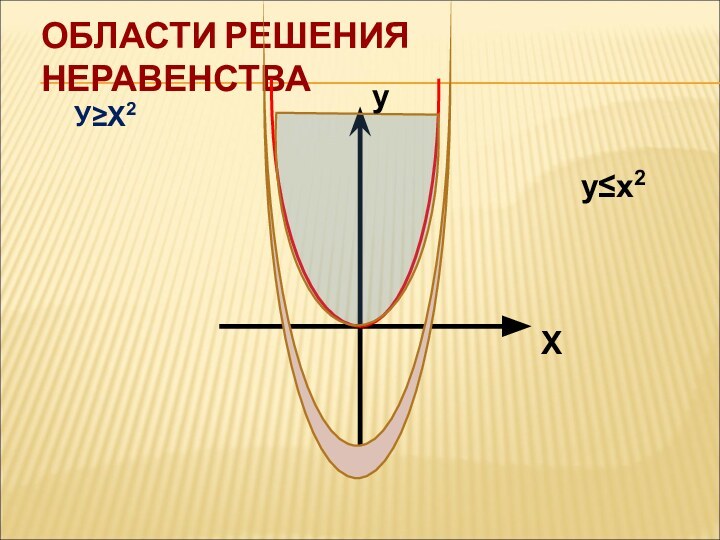
12. ОБЛАСТИ РЕШЕНИЯ НЕРАВЕНСТВАУ≥Х2у≤х2Ху
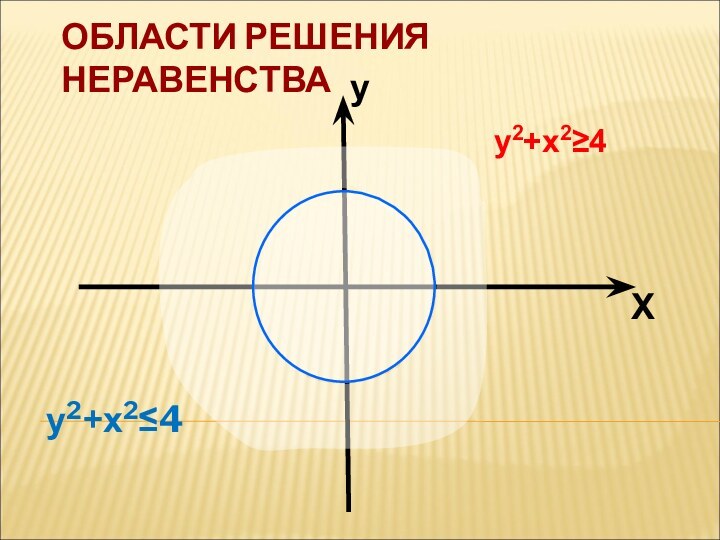
13. ОБЛАСТИ РЕШЕНИЯ НЕРАВЕНСТВАу2+х2≤4 у2+х2≥4 уХ
14. ПРАВИЛО ПРОБНОЙ ТОЧКИ 1. Построить F(x;y)=0
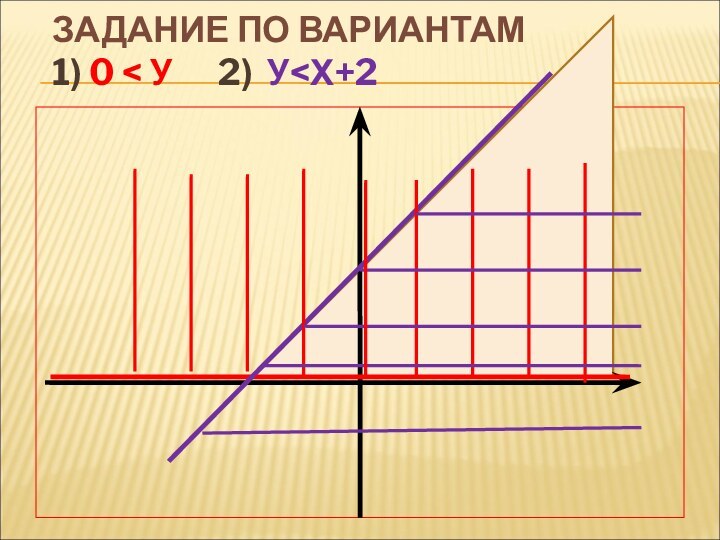
15. ЗАДАНИЕ ПО ВАРИАНТАМ1) 0 < У 2) У
16. ЗАДАНИЕ ПО ВАРИАНТАМСначала ребята пробуют самостоятельно решить
17. ЗАДАНИЕ ПО ВАРИАНТАМ 1) 0 < У 2) У
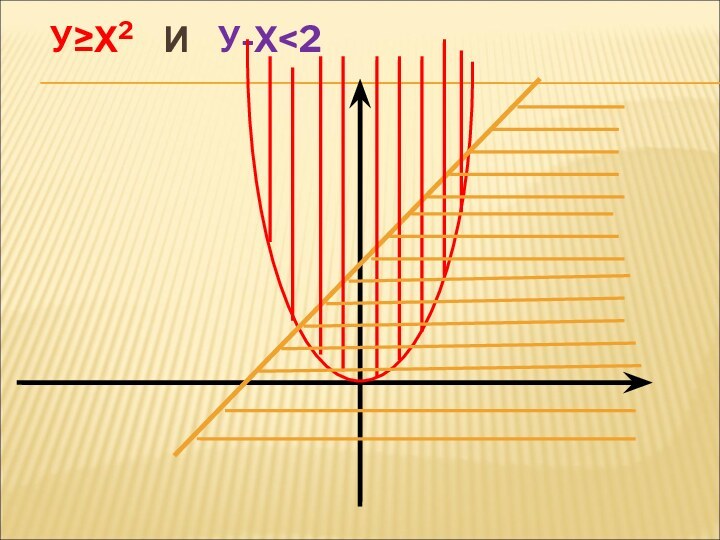
18. У≥Х2 И У-Х
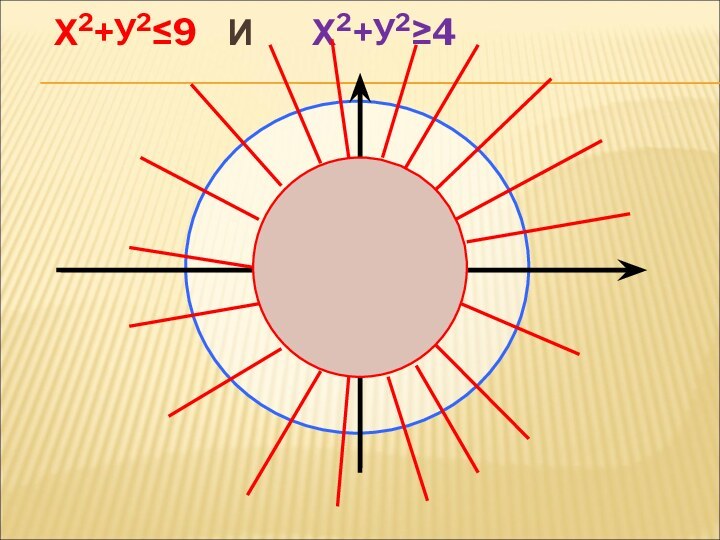
19. Х2+У2≤9 И Х2+У2≥4
20. ПРОВЕРЬ СЕБЯЗадание дано одно всему ряду обучающихся,
21. ПРОВЕРЬ СЕБЯ 1
22. ДОМАШНЕЕ ЗАДАНИЕ1.Придумать свое неравенство и изобразить на
23. Скачать презентацию
24. Похожие презентации

ПРОБЛЕМНЫЙ УРОК ИЗУЧЕНИЯ НОВОГО МАТЕРИАЛА. На предыдущих уроках мы решали системы уравнений графическим способом, системы уравнений аналитическим способом. Сегодня мы переходим к изучению новой темы «Решение неравенств с двумя переменными».Но сначала повторим, как вы усвоили

Главная
Алгебра
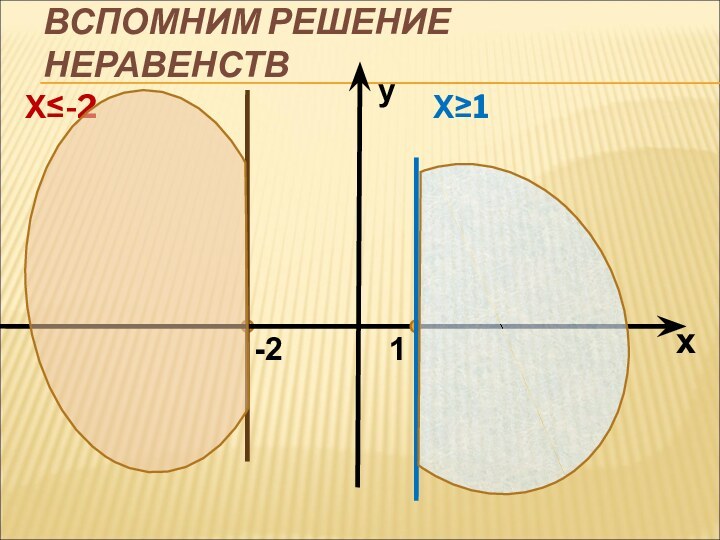
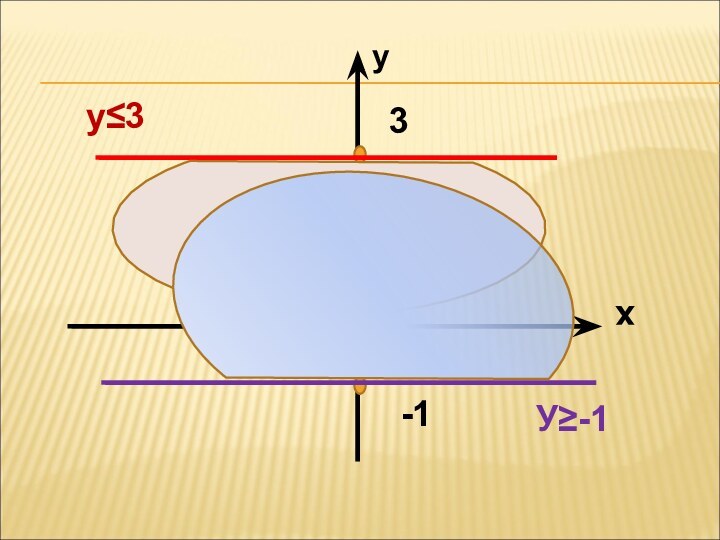
Решение неравенств с двумя переменными

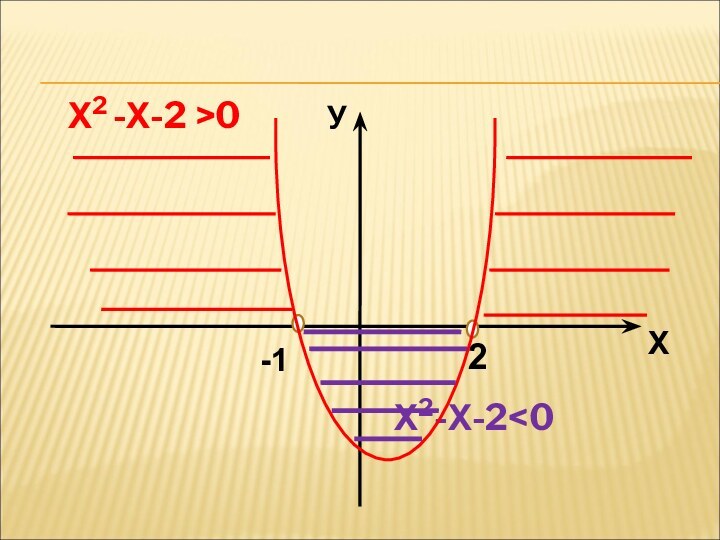
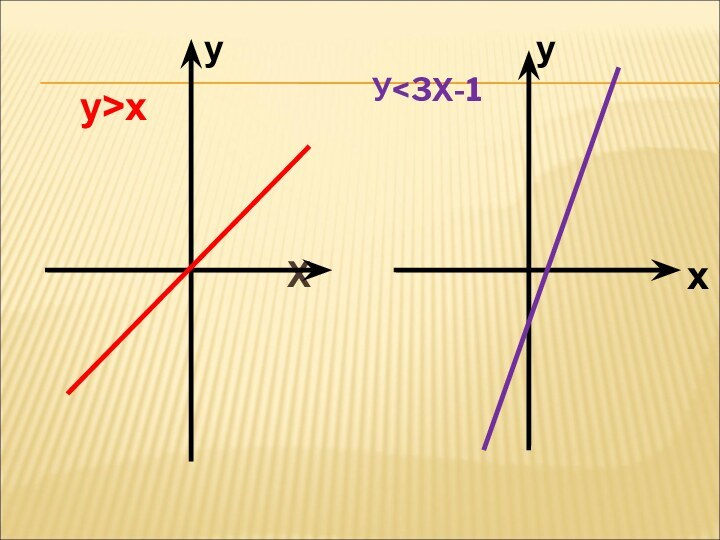
РЕШЕНИЕ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИУрок алгебры 9 классучитель математики Бичурина Надежда Фёдоровна

ПРОБЛЕМНЫЙ УРОК ИЗУЧЕНИЯ НОВОГО МАТЕРИАЛА. На предыдущих уроках мы решали системы

ЦЕЛИ УРОКА:Ввести понятие неравенств с двумя переменнымиСоставить алгоритм решения неравенствФормировать навыки решения неравенств

ЗАПОМНИТЬРешением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное

Подберем пару чисел, которая будет являться решением неравенства с двумя переменными. Построить

ОБЛАСТИ РЕШЕНИЯ НЕРАВЕНСТВАу2+х2≤4 у2+х2≥4 уХ

ПРАВИЛО ПРОБНОЙ ТОЧКИ 1. Построить F(x;y)=0 2.Взяв из каждой области пробную

ЗАДАНИЕ ПО ВАРИАНТАМСначала ребята пробуют самостоятельно решить неравенства. Затем представитель от каждого

ПРОВЕРЬ СЕБЯЗадание дано одно всему ряду обучающихся, можно совещаться, работая парами, можно

ДОМАШНЕЕ ЗАДАНИЕ1.Придумать свое неравенство и изобразить на координатной плоскости множество его решений.

Слайды презентации

Слайд 2 ПРОБЛЕМНЫЙ УРОК ИЗУЧЕНИЯ НОВОГО МАТЕРИАЛА.
На предыдущих уроках

мы решали системы уравнений графическим способом, системы уравнений аналитическим

способом. Сегодня мы переходим к изучению новой темы «Решение неравенств с двумя переменными».Но сначала повторим, как вы усвоили материал прошлого урока. Для этого вспомним графики функций, которые вы изучали.

Слайд 3 ПОВТОРИМ ГРАФИКИ ФУНКЦИЙ.
У=Х2

У=3Х +5

У=Х3 У2+Х2=9 ХУ=8 У=-2Х (Х-2)2+(У+3)2=16

Слайд 4
ВСПОМНИМ РЕШЕНИЕ НЕРАВЕНСТВ
Х≤-2

Х≥1

-2

Слайд 5

-1

у≤3

У≥-1

Слайд 6
Х2 -Х-2 >0

Х2-Х-2<0

-1

Слайд 7 ЦЕЛИ УРОКА:
Ввести понятие неравенств с двумя переменными
Составить алгоритм

решения неравенств
Формировать навыки решения неравенств

Слайд 8 ЗАПОМНИТЬ
Решением неравенства с двумя переменными называется пара значений

ЗАПОМНИТЬРешением неравенства с двумя переменными называется пара значений этих переменных, обращающая

этих переменных, обращающая данное неравенство в верное числовое неравенство.

Слайд 9
Подберем пару чисел, которая будет являться решением неравенства

Подберем пару чисел, которая будет являться решением неравенства с двумя переменными.

с двумя переменными.
Построить в тетради графики функций

У > Х
У < 3Х -1
Проверьте, будет ли являться решением неравенства пара чисел (1;3) (-2;-5)
(5;-4)?

Слайд 10

У<3Х-1

у>х

Слайд 11
А если даны неравенства вида
У >

Х2 или У < Х2
х2+у2 < 4

х2+у2 > 4 Как поступить?
Выслушать предложения учеников.
Ученики самостоятельно предлагают алгоритм решения неравенств.

Слайд 12 ОБЛАСТИ РЕШЕНИЯ НЕРАВЕНСТВА

У≥Х2
у≤х2

Х
у

Слайд 13 ОБЛАСТИ РЕШЕНИЯ НЕРАВЕНСТВА
у2+х2≤4

у2+х2≥4
у
Х

Слайд 14 ПРАВИЛО ПРОБНОЙ ТОЧКИ
1. Построить F(x;y)=0
2.Взяв

из каждой области пробную точку установить, являются ли ее

координаты решением неравенства.
3.Показать область решения неравенства.

Слайд 15 ЗАДАНИЕ ПО ВАРИАНТАМ
1) 0 < У

2) У

2)Х2+У2≥4

Слайд 16 ЗАДАНИЕ ПО ВАРИАНТАМ
Сначала ребята пробуют самостоятельно решить неравенства.

ЗАДАНИЕ ПО ВАРИАНТАМСначала ребята пробуют самостоятельно решить неравенства. Затем представитель от

Затем представитель
от каждого варианта идет к доске и

на одной координатной плоскости показывает решение своего неравенства. Что мы сейчас решили? Учащиеся могут догадаться, что решали систему неравенств.