- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Квадратичная функция, её свойства и график.
Содержание
- 2. В математике есть своя красота, как в живописи и поэзии. (Н.Е.Жуковский)
- 3. y= ax2 +bx + cгде: a,b,c –
- 4. 1. Определить, какие из данных функций являются
- 5. Алгоритм построения параболы у = ах2
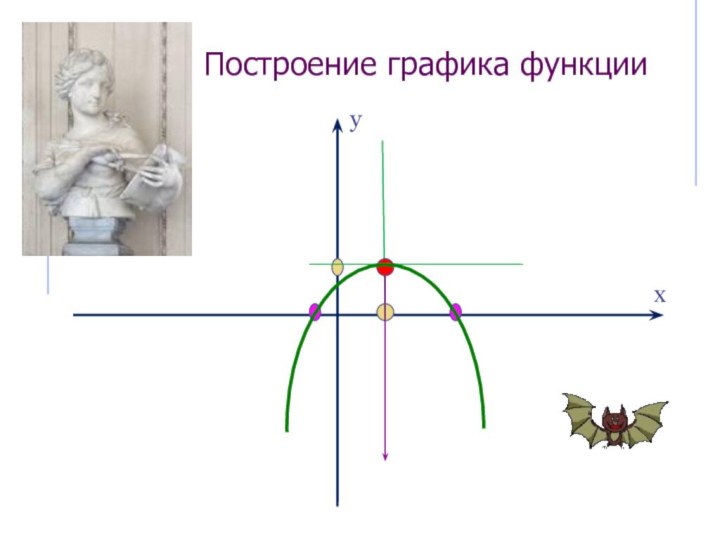
- 6. Построение графика функцииух
- 7. Чтобы построить график функции у =
- 8. Осью параболы будет прямая х = -
- 9. Свойства квадратичной функцииМногие свойства квадратичной функции зависят
- 10. Вспоминаем : Дискриминантом квадратного уравнения ах2 +
- 11. если дискриминант больше нуля, то парабола
- 12.
- 13.
- 14. При - ветви параболы направлены вверх,При ветви параболы направлены внизf(x0)ххуу
- 15. Назовите те параболы, ветви которых будут
- 16. Для закрепления теоретических знаний решим задачу.Задание: Построить график функции :
- 17. Решение :0График функции можно построить двумя способами:
- 18. Построим график у = х2, затем произведем
- 19. Построим график , используя свойства квадратичной функции
- 20. Ось симметрии Область значений функции – Е
- 21. Скачать презентацию
- 22. Похожие презентации














Слайд 3
y= ax2 +bx + c
где: a,b,c –
числа
Х – независимая переменная
а 0Определение квадратичной функции
Квадратичной функцией называется функция , которую можно задать формулой вида:
Слайд 4
1. Определить, какие из данных функций являются квадратичными:
у
= - ( х + 3 ) 2 +
2у = 5х + 2
у = х2 – 1
у = 6х3 – 5х2 + 7
у = 7х2 + 2х -1
у = 5х2 + 3х
А ТЕПЕРЬ НЕБОЛЬШОЙ ТЕСТ
у = х2 – 5х + 6
у = 6х4 + 5х2 + 7
Слайд 5 Алгоритм построения параболы у = ах2 +
bх + с :
Найти координаты вершины параболы, построить на
координатной плоскости соответствующую точку, провести ось симметрии.Определить направление ветвей параболы.
Найти координаты еще нескольких точек , принадлежащих искомому графику ( в частности, координаты точки пересечения параболы с осью у и нули функции, если они существуют).
Отметить на координатной плоскости найденные точки и соединить их плавной линией.
График любой квадратичной функции – парабола.
Слайд 7 Чтобы построить график функции у = ах2
+ bx + с,
надо выполнить параллельный перенос параболы
у = ах2, чтобы вершина оказалась в точке ( x0 ; y0 )
Слайд 8
Осью параболы будет прямая
х = -
Вершина
параболы - ( х0; уо) ,
где :
хо = - у0 =Графиком квадратичной функции
у = ах2 + bх + с является парабола, которая получается из параболы
у = ах2 параллельным переносом.
.
-
Таким образом:
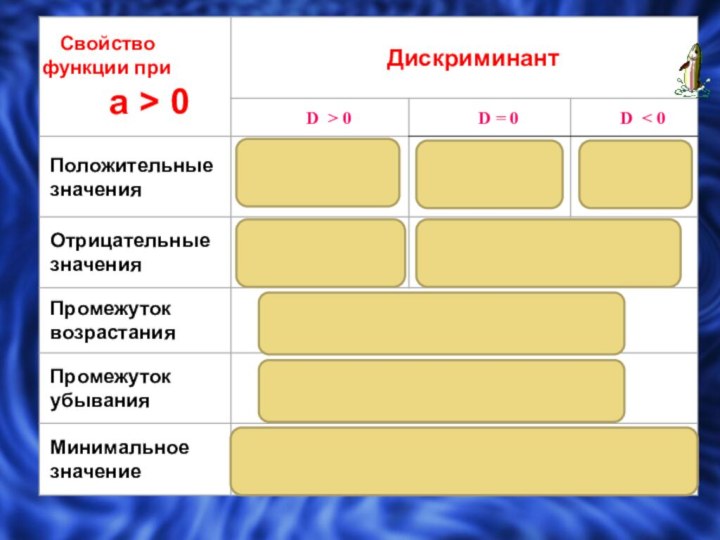
Слайд 9
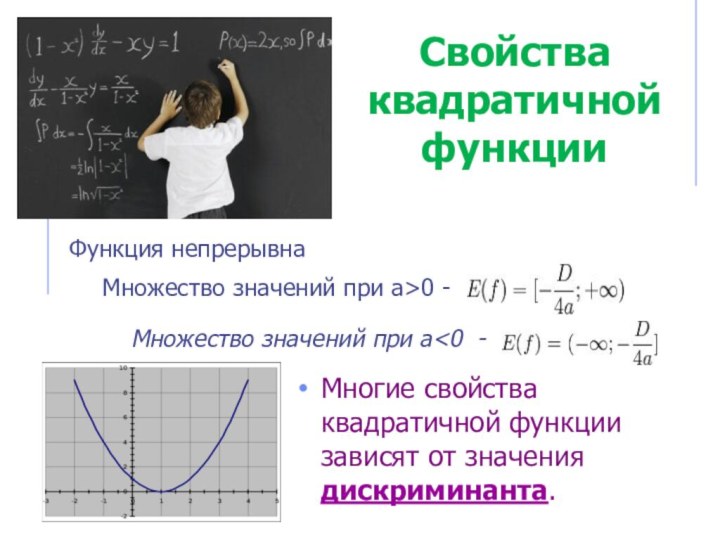
Свойства квадратичной функции
Многие свойства квадратичной функции зависят от
значения дискриминанта.
Функция непрерывна
Множество значений при a>0 -
Множество
значений при a<0 -
Слайд 10
Вспоминаем :
Дискриминантом квадратного уравнения ах2 + bх
+ с = 0 называется выражение
b2 – 4acЕго обозначают буквой D, т.е. D= b2 – 4ac.
Возможны три случая:
D 0
D 0
D 0
Слайд 11
если дискриминант больше нуля, то парабола пересекает
ось абсцисс в двух точках,
если дискриминант равен нулю,
то парабола касается оси абсцисс,если дискриминант меньше нуля, то парабола не пересекает ось абсцисс,
если старший коэффициент квадратного трёхчлена (а) равен нулю, то графиком функции является не парабола, а прямая; (и соответствующее уравнение надо решать не как квадратное, а как линейное),
абсцисса вершины параболы равна
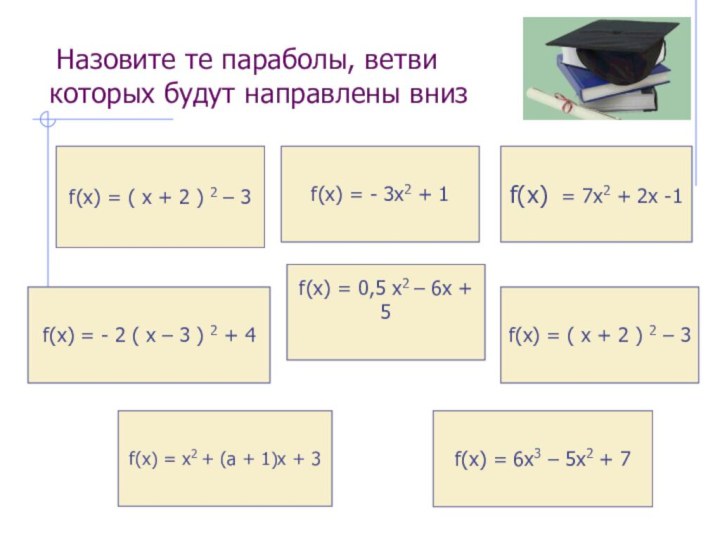
Слайд 15 Назовите те параболы, ветви которых будут направлены
вниз
f(x) = - 2 ( х – 3 )
2 + 4f(x) = 7х2 + 2х -1
f(x) = ( х + 2 ) 2 – 3
f(x) = х2 + (а + 1)х + 3
f(x) = 0,5 х2 – 6х + 5
f(x) = 6х3 – 5х2 + 7
f(x) = ( х + 2 ) 2 – 3
f(x) = - 3х2 + 1
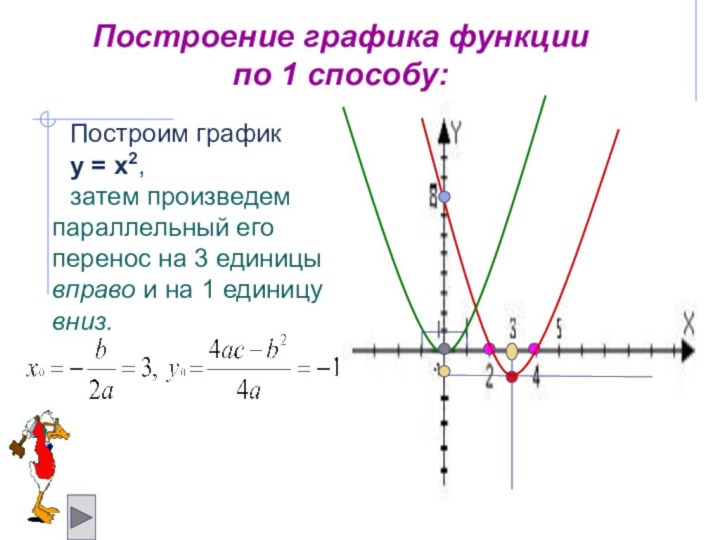
Слайд 18
Построим график
у = х2,
затем произведем параллельный
его перенос на 3 единицы вправо и на 1
единицу вниз.Построение графика функции по 1 способу:
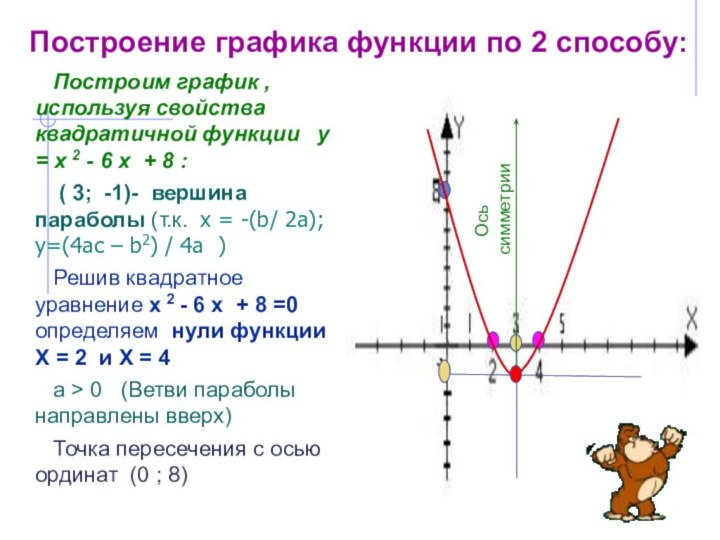
Слайд 19 Построим график , используя свойства квадратичной функции
у = х 2 - 6 х + 8
:( 3; -1)- вершина параболы (т.к. х = -(b/ 2a); y=(4ac – b2) / 4a )
Решив квадратное уравнение х 2 - 6 х + 8 =0 определяем нули функции Х = 2 и Х = 4
а > 0 (Ветви параболы направлены вверх)
Точка пересечения с осью ординат (0 ; 8)
Построение графика функции по 2 способу:
Ось симметрии
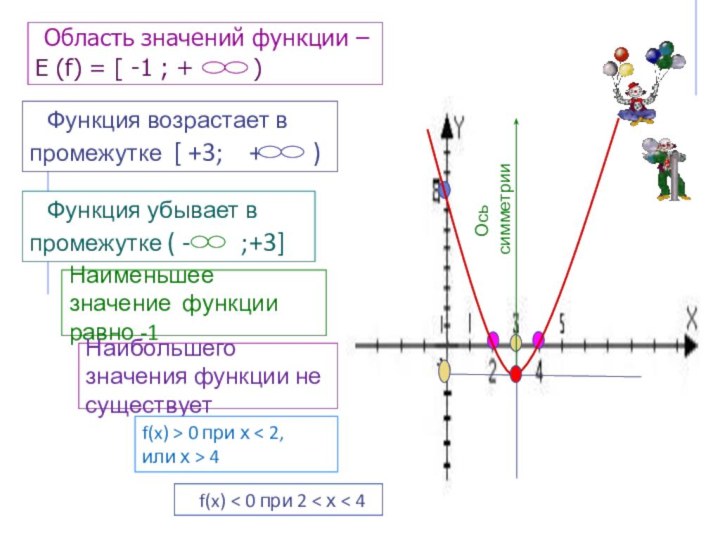
Слайд 20
Ось симметрии
Область значений функции – Е (f)
= [ -1 ; + )
Функция
возрастает в промежутке [ +3; + ) Функция убывает в промежутке ( - ;+3]
Наименьшее значение функции равно -1
Наибольшего значения функции не существует
f(x) > 0 при х < 2, или х > 4
f(x) < 0 при 2 < х < 4