способы задания функции. Ввести понятие чётной и нечётной функции.
Освоить основные способы преобразования графиков.Воспитание интереса к математике.
Развитие зрительного восприятия предмета.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть













D
E
y
x
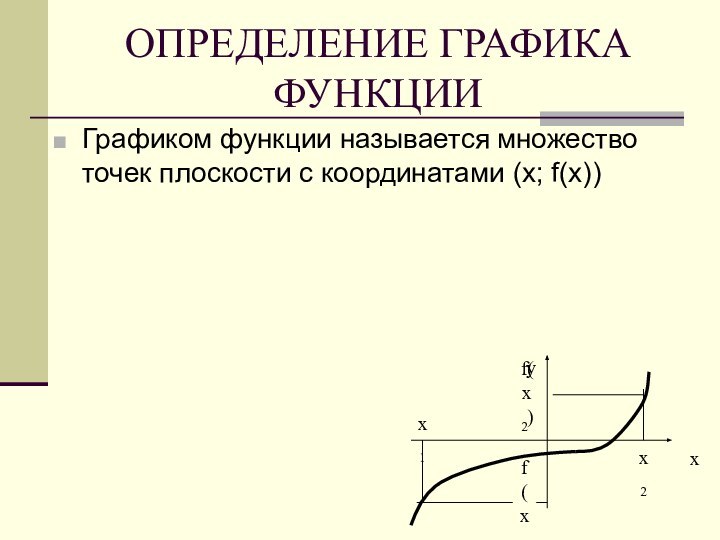
y = f (x)
у(х) =
у
х1
f(х1)
х2
f(х2)
х
у=√х
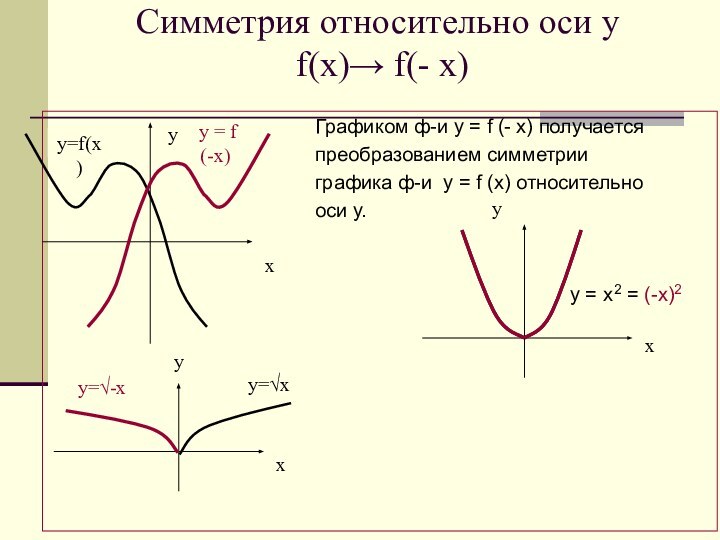
у = f (-х)
у
у
у
х
х
х
у=f(х)
у=√-х
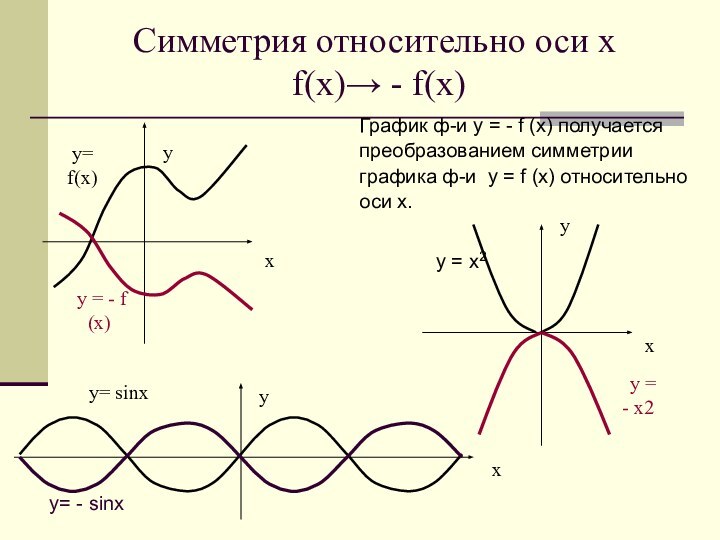
у= f(х)
у = - х2
у = - f (х)
у= sinx
у
у
у
х
х
х
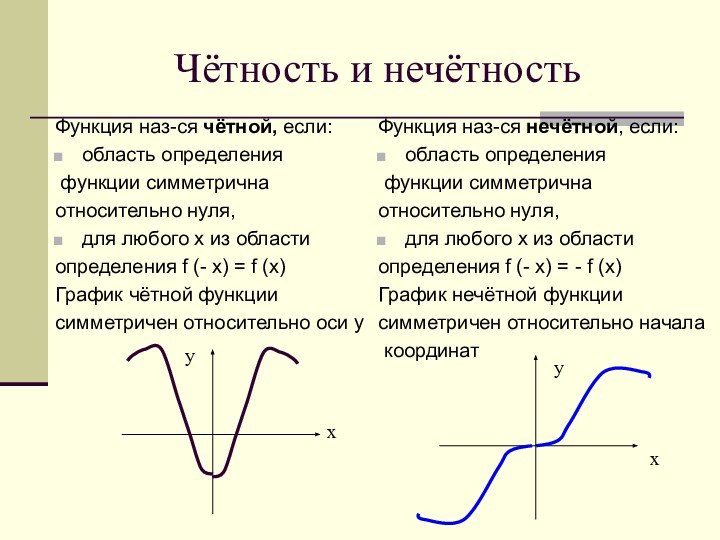
Функция наз-ся нечётной, если:
область определения
функции симметрична
относительно нуля,
для любого х из области
определения f (- х) = - f (х)
График нечётной функции
симметричен относительно начала
координат
х
у
х
у
у=х2
у
у
у
х
х
х
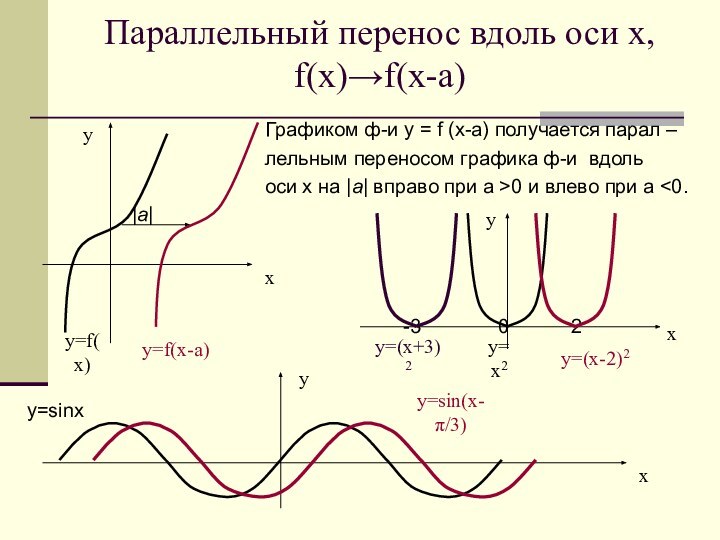
у=(х+3)2
у=(х-2)2
у=f(x-а)
у=f(x)
у=sin(x-π/3)
х
х
х
у
у
у
у=sinx
у=sinx+1
у=f(x)
у=х2 -2
у=х2+1
|b|
х
х
х
у
у
у
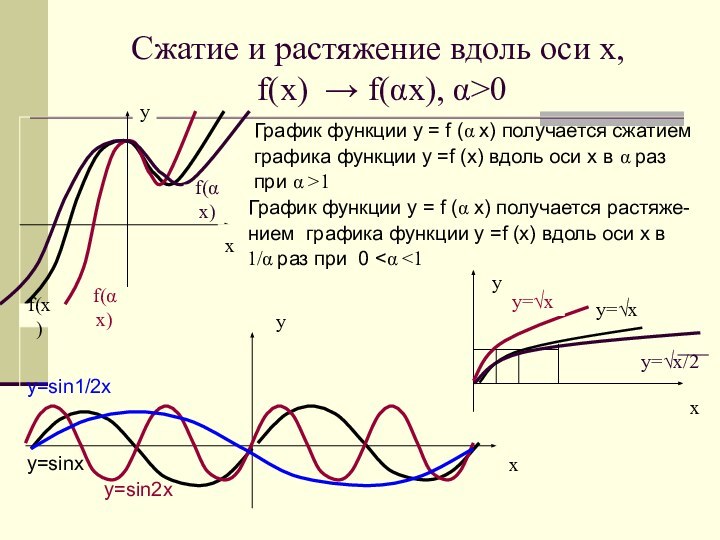
f(αx)
f(αx)
f(x)
у=√х
у
у
у=sinx
х
х
х
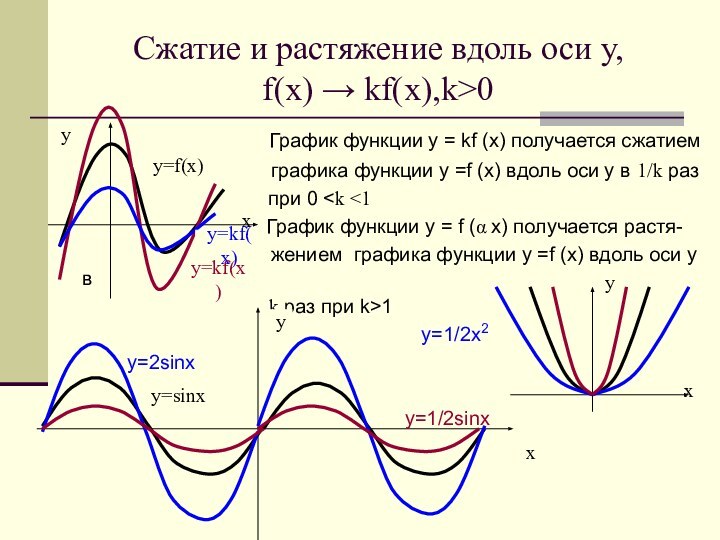
у=kf(x)
у=kf(x)
у=f(x)
у
у
у
у
х
х
х
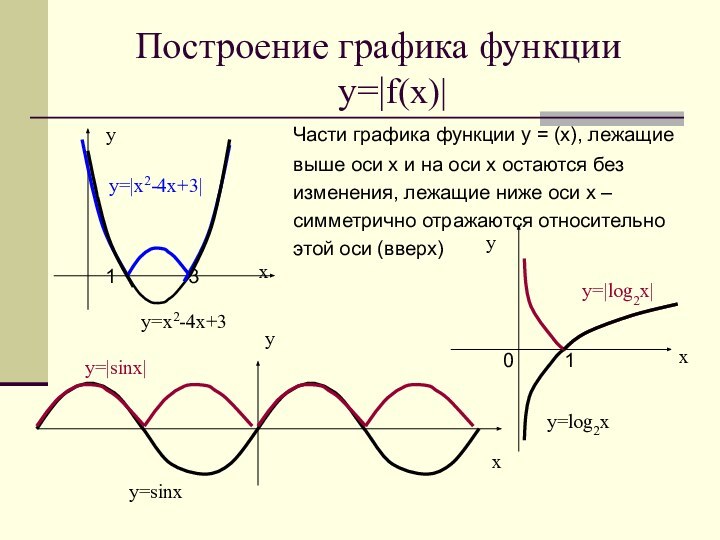
y=|log2x|
y=|x2-4x+3|
y=|sinx|
y=log2x
y=sinx
y=x2-4x+3
у
у
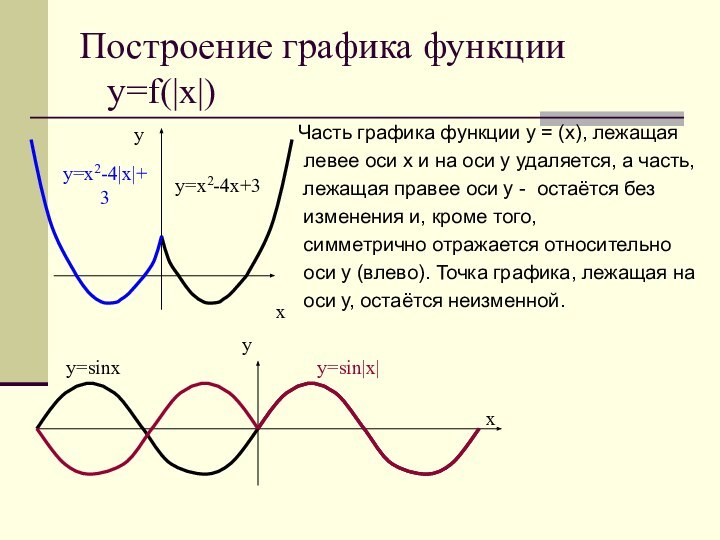
y=x2-4|x|+3
х
х
y=x2-4x+3
y=sinx
y=sin|x|
у
у
у
х
х
х
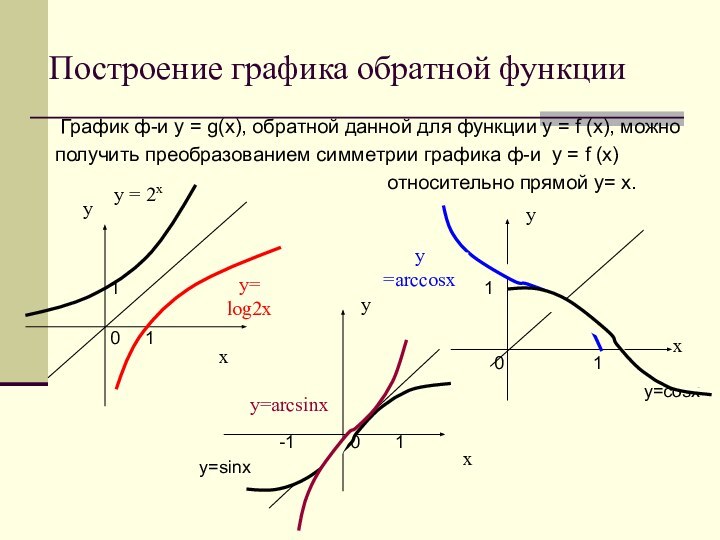
у = 2х
y= log2x
y=arcsinx
y =arccosx