- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Степенная функция
Содержание
- 2. р=2n р - чётное число у = х 2n
- 3. — область определения — все
- 4. р - нечётное число р=2n-1 у = х 2n-1
- 5. Свойства функции у = х 2n-1 —
- 6. График функции y = xр, где p
- 7. 1. Область определения: Х ≥ 02. Множество
- 8. p – положительное действительное нецелое число Пример:
- 9. Свойства функции 1.Область определения: x ≥ 0;2.Множество
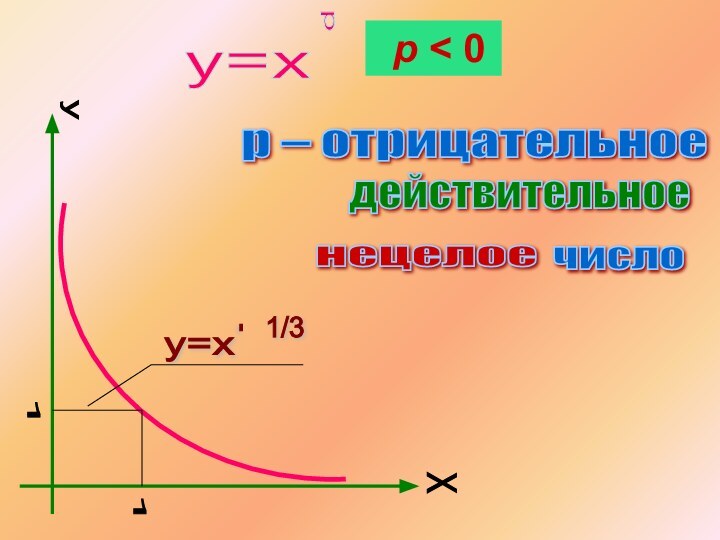
- 10. p – отрицательное действительное нецелое число p < 0
- 11. Скачать презентацию
- 12. Похожие презентации
р=2n р - чётное число у = х 2n

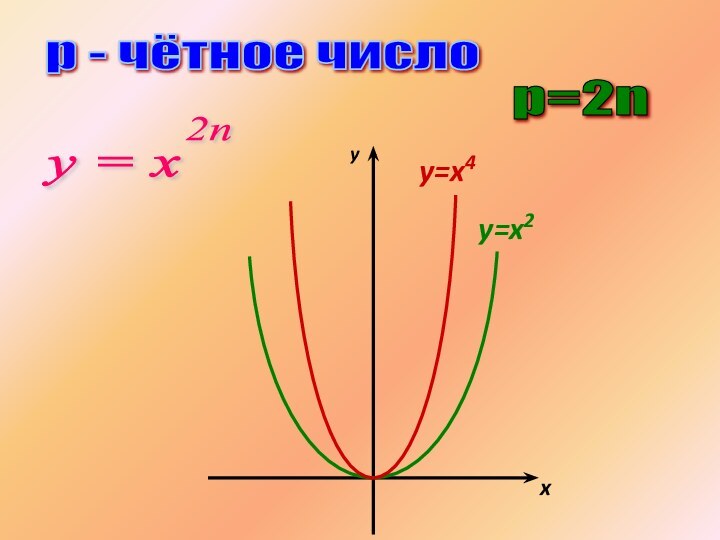






Слайд 3 — область определения — все действительные
числа, т.е. множество R;
— множество значений — неотрицательные числа,
т. е. у ≥ 0;— функция у = х2n четная, так как
(-х)2n = х2n;
— функция является убываю-
щей на промежутке х ≤ 0,
возрастающей
на промежутке х ≥ 0.
Свойства функции
у = х
2n
Слайд 5
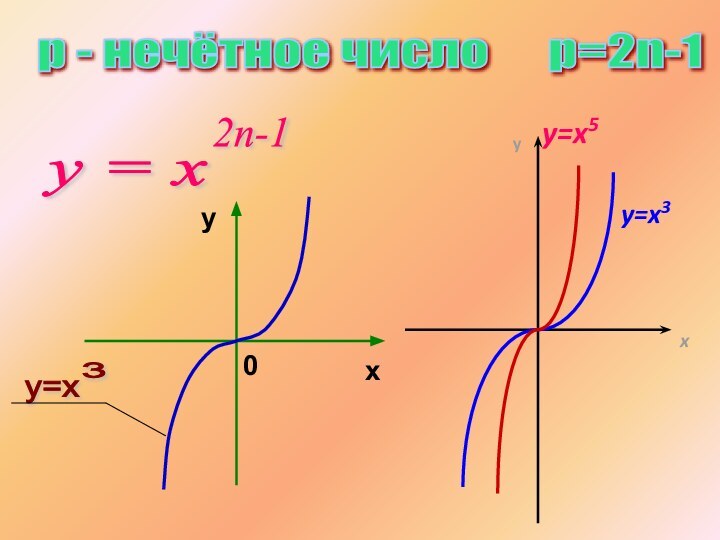
Свойства функции
у = х
2n-1
— область
определения — все действительные числа, т.е. множество
R;— множество значений — все действительные числа, т.е. множество R;
— функция у = х2n-1 нечетная, так как (-х)2n-1 = -х2n-1;
— функция является
возрастающей
на промежутке х € R.
Слайд 6 График функции y = xр, где p –
положительное нецелое число, имеет такой же вид, как, например,
график функцииy = x1/3 (при 0< p <1).
p – положительное
действительное
нецелое
число
0< p <1
Слайд 7
1. Область определения: Х ≥ 0
2. Множество значений:
У ≥ 0
3. Нули функции при х=0
4. Функция
является возрастающейна промежутке X ≥ 0
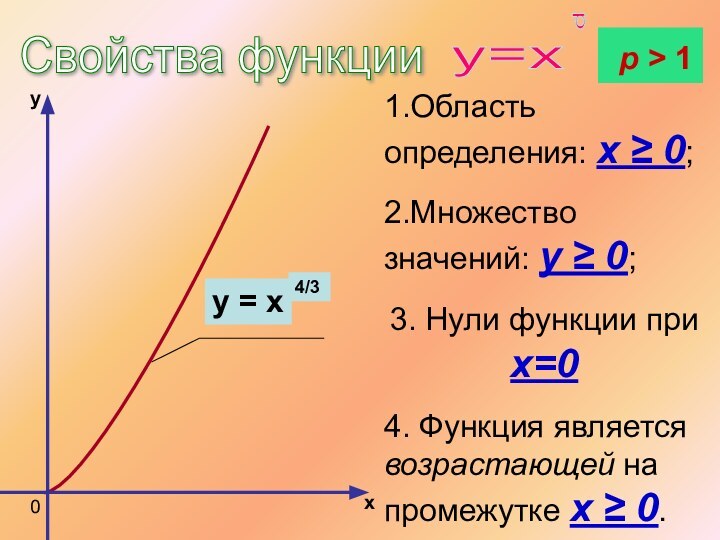
Свойства функции
0< p <1
р – положительное действительное нецелое число.
Слайд 8
p – положительное
действительное
нецелое
число
Пример:
График
функции
y = xр, где p – положительное нецелое
число, имеет такой же вид, как, например, график функции y = x4/3 (при p >1). p > 1
Слайд 9
Свойства функции
1.Область определения: x ≥ 0;
2.Множество значений:
y ≥ 0;
3. Нули функции при х=0
4. Функция является
возрастающей на промежутке x ≥ 0. p > 1