- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Кривые второго порядка
Содержание
- 2. ИСТОРИЧЕСКАЯ СПРАВКАВпервые кривые второго порядка изучались одним
- 3. В истории развития учения о кривых этот
- 4. Окружность
- 5. Окружность' — геометрическое место точек плоскости, равноудалённых
- 6. Эллипс
- 7. Эллипс (др.-греч. — опущение, недостаток, в смысле
- 8. Окружность является частным случаем эллипса. Наряду с
- 9. Парабола
- 10. Парабола (греч. — приложение) — геометрическое место
- 11. Оптическое свойство. Пучок лучей, параллельных оси параболы,
- 12. Наряду с эллипсом и гиперболой, парабола является
- 13. Гипербола
- 14. Гипербола (др.-греч. — «бросать», «сверх») — геометрическое
- 15. Наряду с эллипсом и параболой, гипербола является
- 16. Коническое сечение или коника есть пересечение плоскости
- 17. Кривая второго порядка называется вырожденной, если Δ
- 19. Скачать презентацию
- 20. Похожие презентации
ИСТОРИЧЕСКАЯ СПРАВКАВпервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же пересечь эту














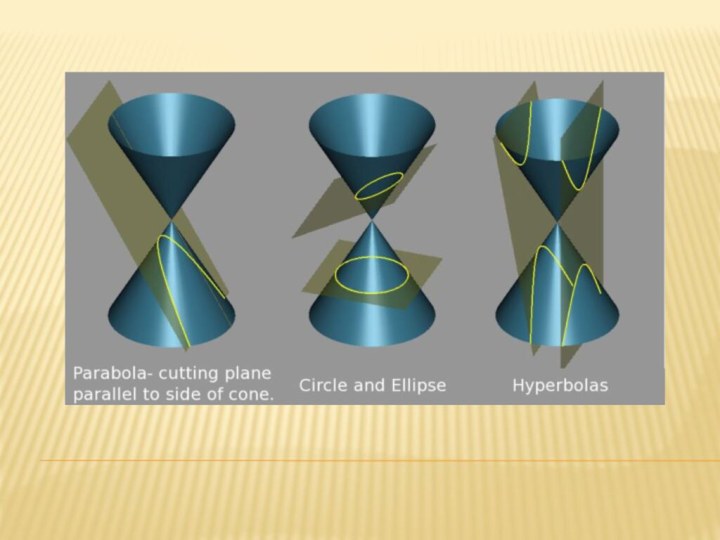

Слайд 3 В истории развития учения о кривых этот способ
является первым. Греки определяли кривые второго порядка как сечения
кругового конуса.Таково же происхождение кривых Персея, получаемых в результате сечений плоскостью поверхности тора. Эвольвента круга может быть определена как линия пересечения поверхности касательных к винтовой линии, перпендикулярной к её оси и т.д.
Однако эти научные знания нашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической.
Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а по достижении второй космической скорости тело по параболе покинет поле притяжения Земли.
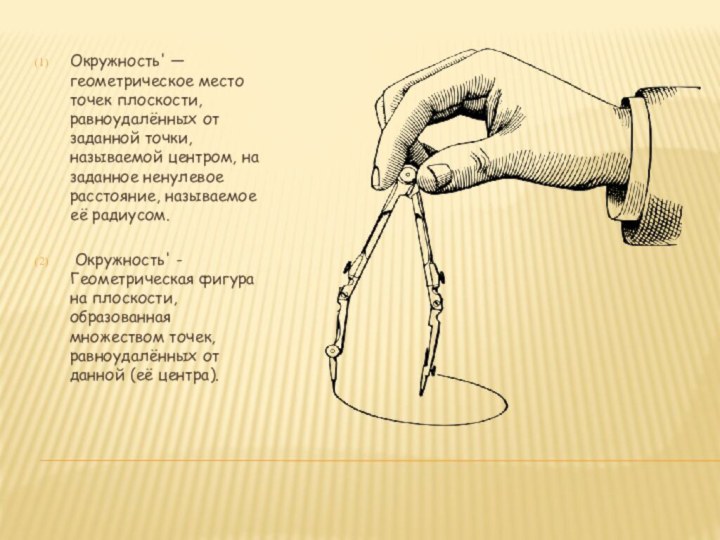
Слайд 5 Окружность' — геометрическое место точек плоскости, равноудалённых от
заданной точки, называемой центром, на заданное ненулевое расстояние, называемое
её радиусом.Окружность' - Геометрическая фигура на плоскости, образованная множеством точек, равноудалённых от данной (её центра).
Слайд 7 Эллипс (др.-греч. — опущение, недостаток, в смысле недостатка
эксцентриситета до 1) — геометрическое место точек M Евклидовой
плоскости.Для которых сумма расстояний до двух данных точек F1 и F2 (называемых фокусами) постоянна и больше расстояния между фокусами, то есть
| F1M | + | F2M | = 2a, причем | F1F2 | < 2a.
Слайд 8 Окружность является частным случаем эллипса. Наряду с гиперболой
и параболой, эллипс является коническим сечением и квадрикой.
Эллипс
также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.Слайд 10 Парабола (греч. — приложение) — геометрическое место точек,
равноудалённых от данной прямой (называемой директрисой параболы) и данной
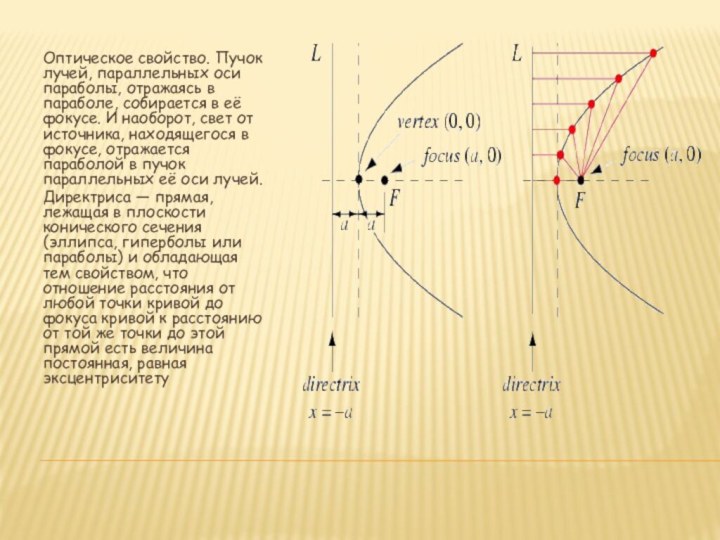
точки (называемой фокусом параболы)Слайд 11 Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь
в параболе, собирается в её фокусе. И наоборот, свет
от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей.Директриса — прямая, лежащая в плоскости конического сечения (эллипса, гиперболы или параболы) и обладающая тем свойством, что отношение расстояния от любой точки кривой до фокуса кривой к расстоянию от той же точки до этой прямой есть величина постоянная, равная эксцентриситету
Слайд 12 Наряду с эллипсом и гиперболой, парабола является коническим
сечением. Она может быть определена как коническое сечение с
единичным эксцентриситетом.Слайд 14 Гипербола (др.-греч. — «бросать», «сверх») — геометрическое место
точек M Евклидовой плоскости, для которых абсолютное значение разности
расстояний от M до двух выделенных точек F1 и F2 (называемых фокусами) постоянно. Точнее,│|F1M| ─ |F2 M|│= 2aпричем | F1 F2 | > 2a > 0.
Слайд 15 Наряду с эллипсом и параболой, гипербола является коническим
сечением и квадрикой. Гипербола может быть определена как коническое
сечение с эксцентриситетом, большим единицы.Квадрика — проективное алгебраическое многообразие, которое можно задать однородным квадратным уравнением
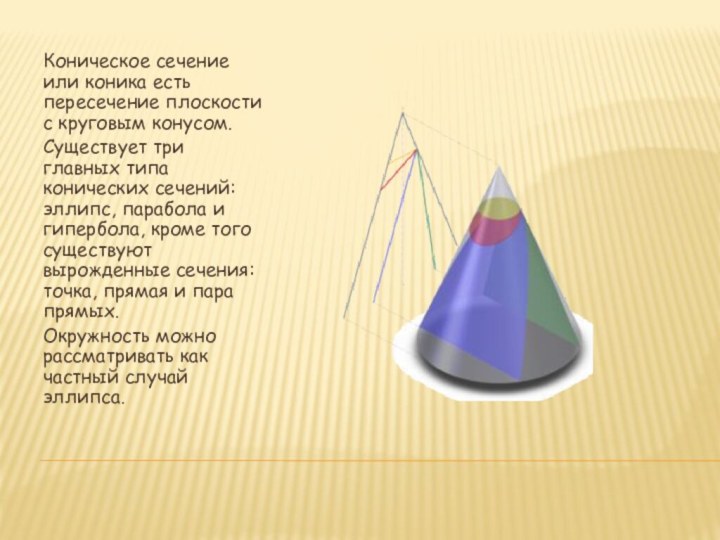
Слайд 16 Коническое сечение или коника есть пересечение плоскости с
круговым конусом.
Существует три главных типа конических сечений: эллипс,
парабола и гипербола, кроме того существуют вырожденные сечения: точка, прямая и пара прямых. Окружность можно рассматривать как частный случай эллипса.
Слайд 17 Кривая второго порядка называется вырожденной, если Δ =
0. Могут возникать следующие варианты:
вещественная точка
на пересечении двух мнимых прямых (вырожденный эллипс) — при условии D > 0;пара вещественных пересекающихся прямых (вырожденная гипербола) — при условии D < 0;
вырожденная парабола — при условии D = 0:
пара вещественных параллельных прямых — при условии B < 0;
одна вещественная прямая (две слившиеся параллельные прямые) — при условии B = 0;
пара мнимых параллельных прямых (ни одной вещественной точки) — при условии B > 0.