достаточные условия убывания и возрастания функций.
Правило отыскания интервалов монотонности.
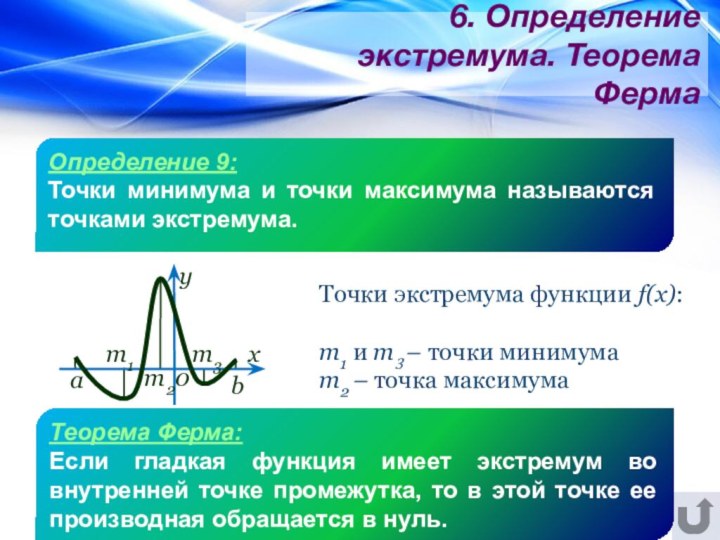
Определение
экстремума. Теорема Ферма.Правило отыскания экстремума.
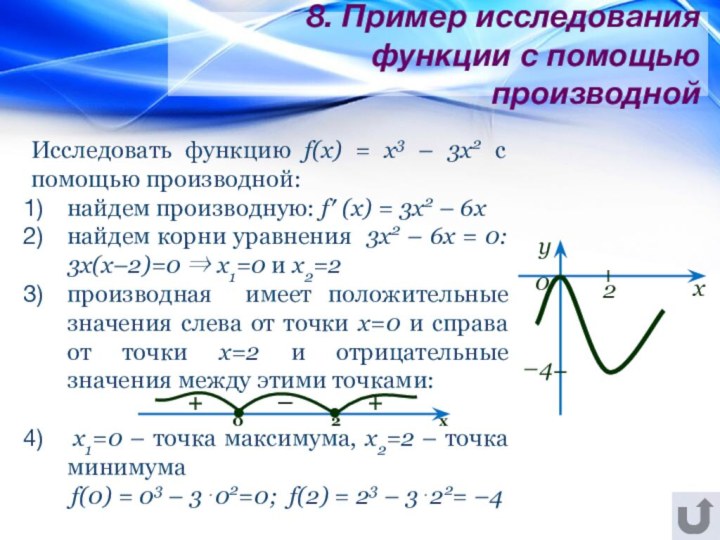
Пример исследования функции с помощью производной.
Источники получения информации.