- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Свойства функций
Содержание
- 2. Схема исследования:Область определенияМножество значенийНули функцииИнтервалы знакопостоянстваПромежутки монотонностиТочки экстремумаНабольшее и наименьшее значения функции
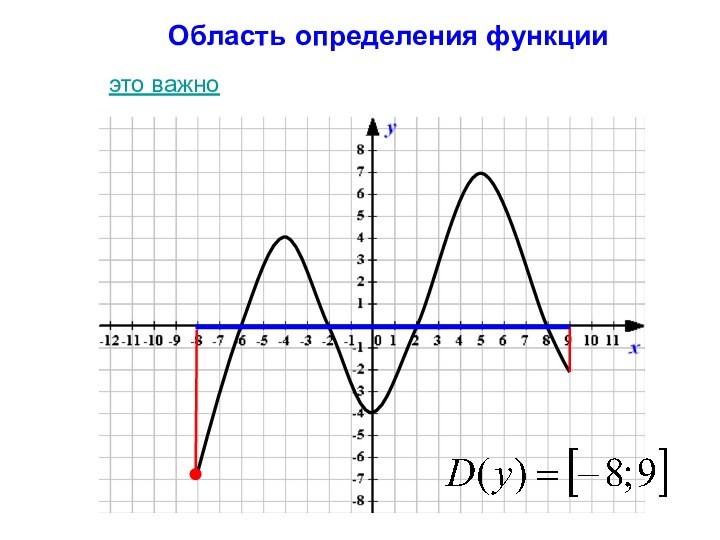
- 3. Область определения функцииэто важно
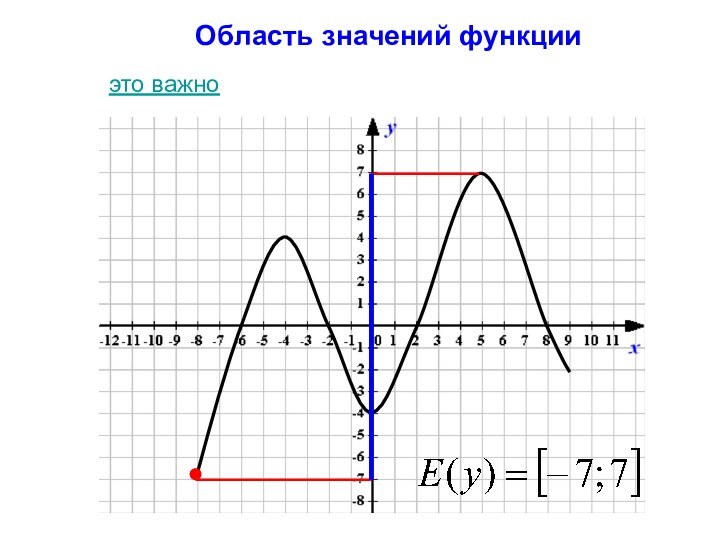
- 4. Область значений функцииэто важно
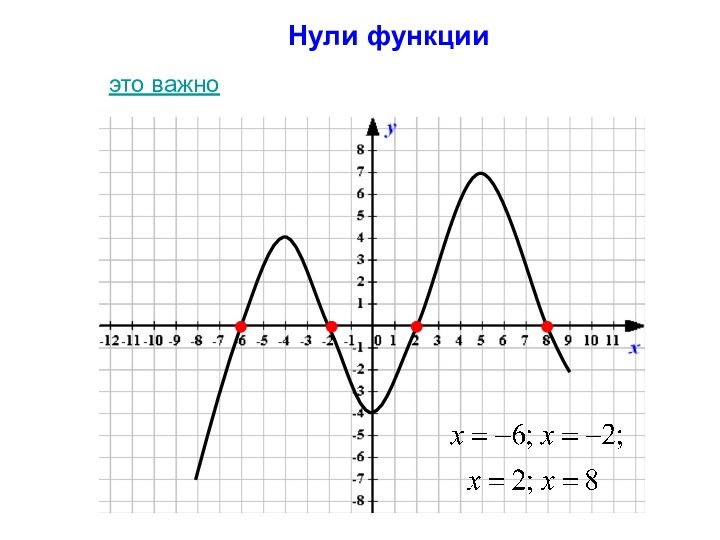
- 5. Нули функцииэто важно
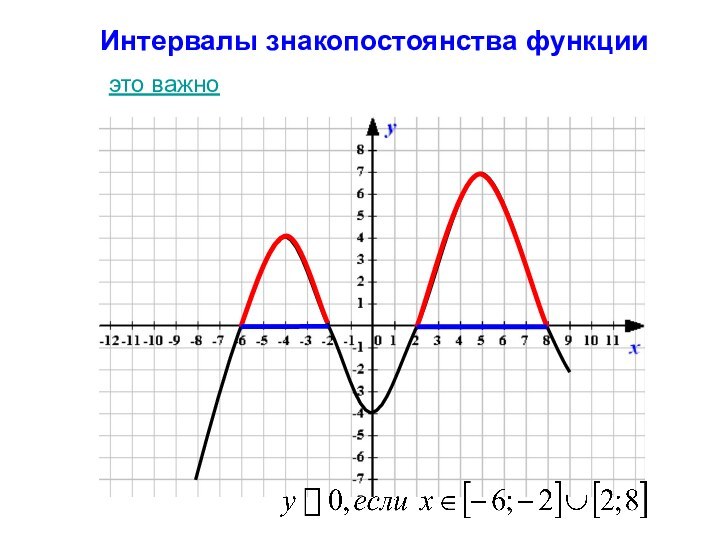
- 6. Интервалы знакопостоянства функцииэто важно
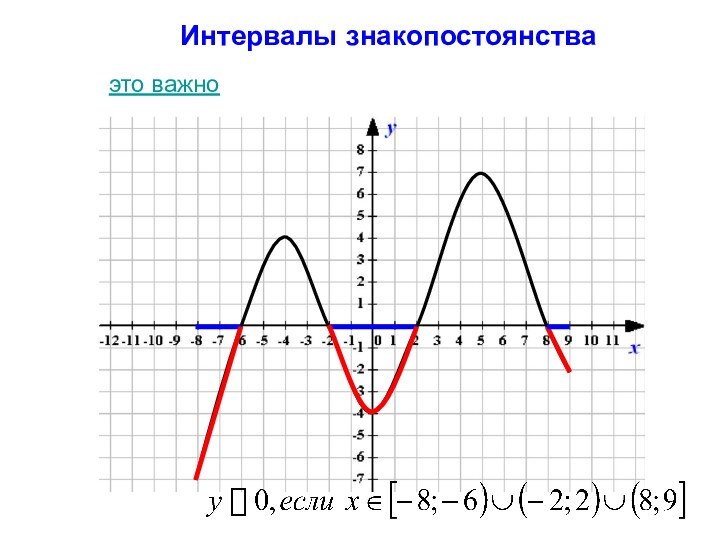
- 7. Интервалы знакопостоянстваэто важно
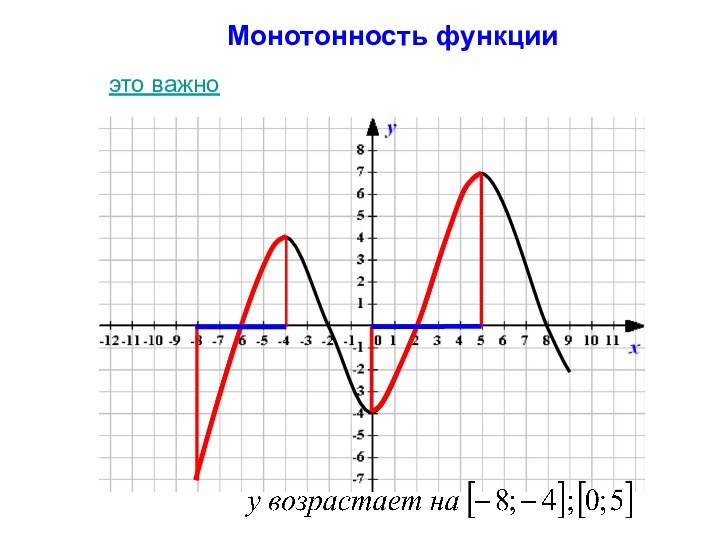
- 8. Монотонность функцииэто важно
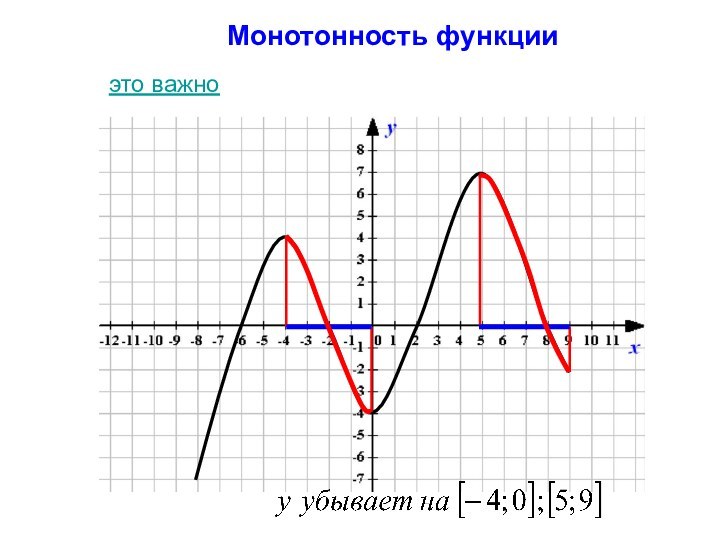
- 9. Монотонность функцииэто важно
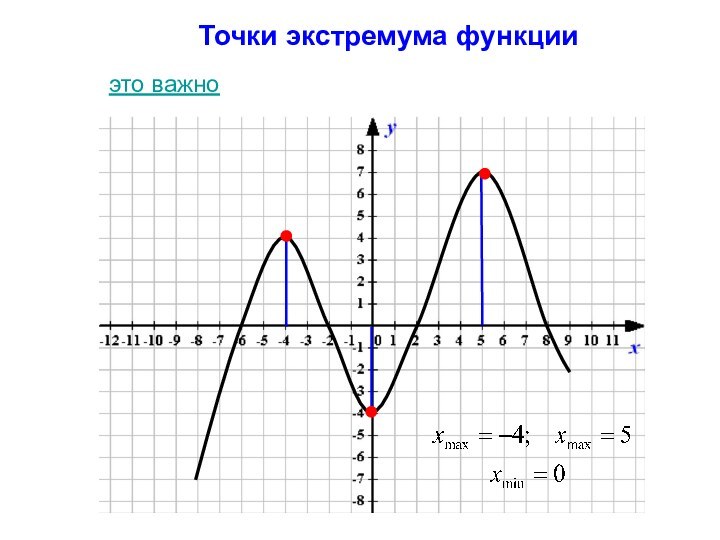
- 10. Точки экстремума функцииэто важно
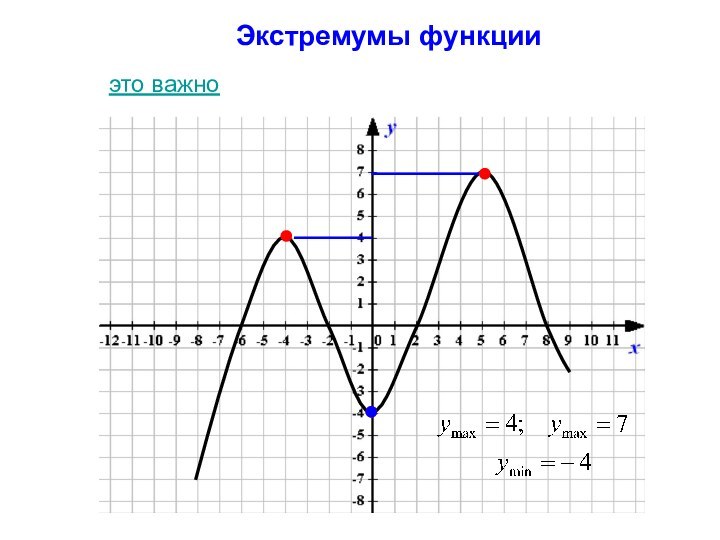
- 11. Экстремумы функцииэто важно
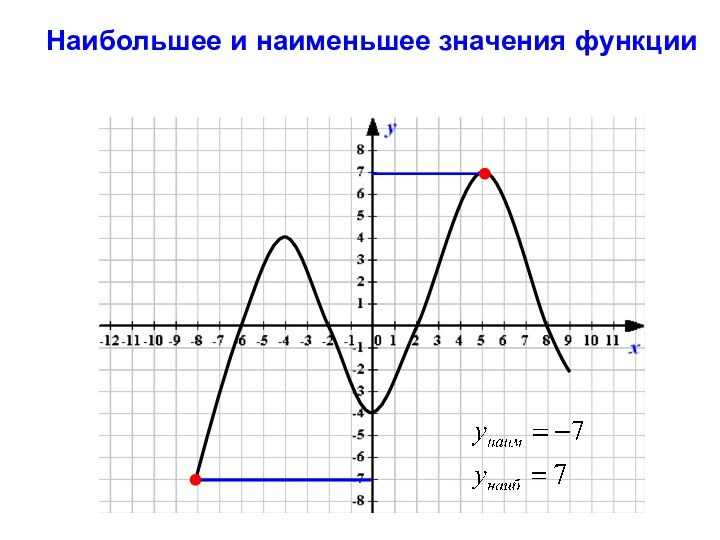
- 12. Наибольшее и наименьшее значения функции
- 17. Область определения функцииВсе допустимые значения аргумента x функции y(х).назад
- 18. Область значения функцииМножество, состоящее из всех чисел y(x), таких, что x принадлежит области определения функции y(х).назад
- 19. Нули функцииЭто значения аргумента х, при которых значение функции у(х) равно нулю. назад
- 20. Интервалы знакопостоянства функцииЭто промежутки, на которых функция y(х) принимает положительные (отрицательные) значения.назад
- 21. Монотонность функцииФункция y(х) убывает на множестве P,
- 22. Точки экстремума функцииТочка x0 называется точкой минимума
- 23. Скачать презентацию
- 24. Похожие презентации
Схема исследования:Область определенияМножество значенийНули функцииИнтервалы знакопостоянстваПромежутки монотонностиТочки экстремумаНабольшее и наименьшее значения функции


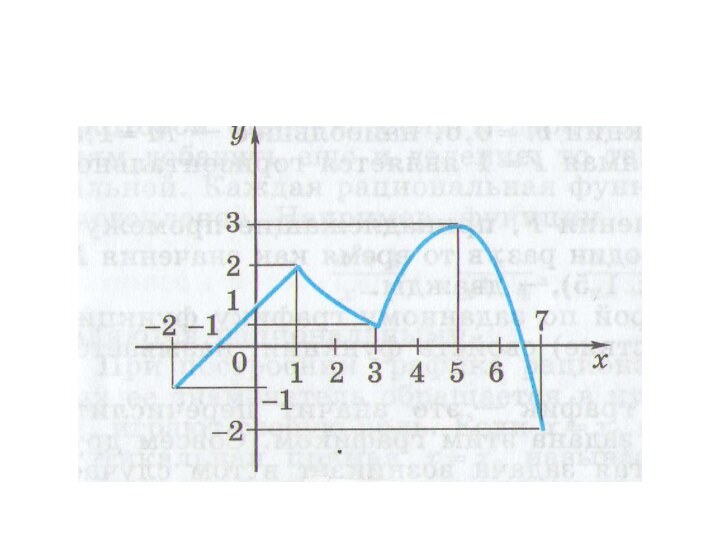
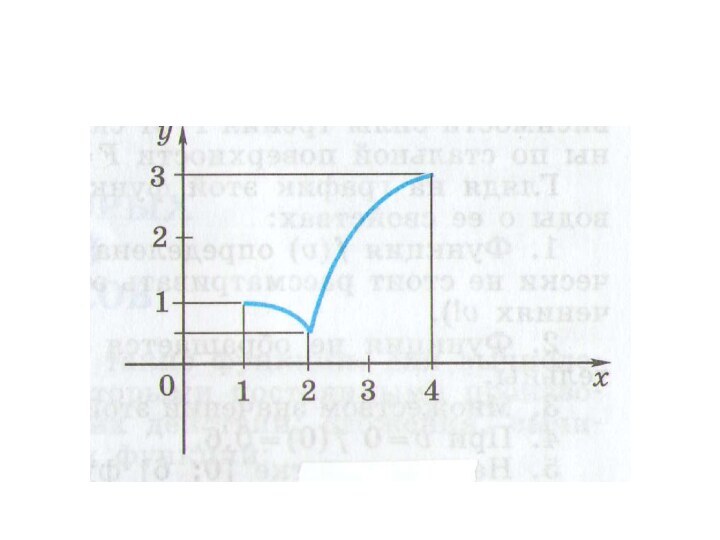
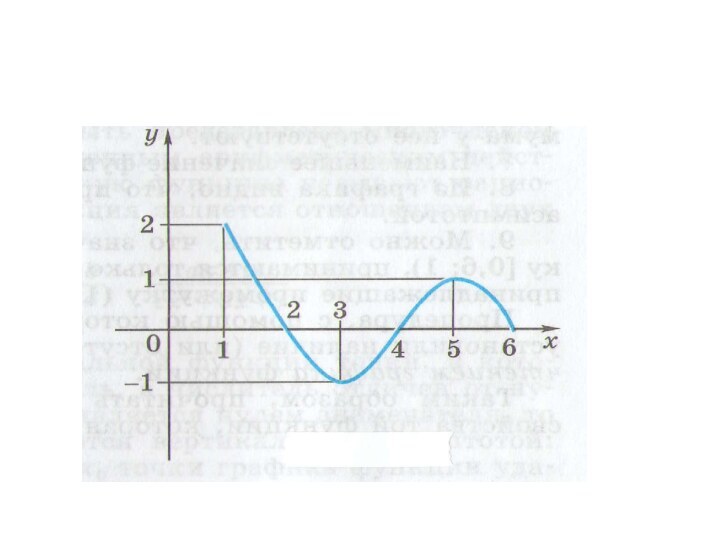







Слайд 2
Схема исследования:
Область определения
Множество значений
Нули функции
Интервалы знакопостоянства
Промежутки монотонности
Точки экстремума
Набольшее
и наименьшее значения функции
Слайд 18
Область значения функции
Множество, состоящее из всех чисел y(x),
таких, что x принадлежит области определения функции y(х).
назад
Слайд 20
Интервалы знакопостоянства функции
Это промежутки, на которых функция
y(х)
принимает положительные (отрицательные) значения.
назад
Слайд 21
Монотонность функции
Функция y(х) убывает на множестве P, если
для любых x1 и x2 из множества P
(x1
< x2), выполнено неравенство y (x2) < y (x1)
назад
Функция y(х) возрастает на множестве P, если для любых x1 и x2 из множества P
(x1 < x2), выполнено неравенство
y (x2) > y (x1)
назад
Слайд 22
Точки экстремума функции
Точка x0 называется точкой минимума функции
y(х), если для всех x из некоторой окрестности x0
выполнено неравенствоназад
Точка x0 называется точкой максимума функции y(х), если для всех x из некоторой окрестности x0 выполнено неравенство