Слайд 2
Содержание
Определение промежутков возрастания и убывания функции (исследование функции
на монотонность)
Нахождение точек экстремума функции
Построение графиков функций
Нахождение наибольшего и
наименьшего значений функции
Работа с графиками функций
Проверь себя
Слайд 3
Исследование функции на монотонность
(т.е. определение
промежутков
возрастания и убывания функции).
Слайд 4
Исследовать функцию на монотонность – это значит выяснить,
на каких промежутках из области определения
функция возрастает,
а на каких – убывает.
Слайд 6
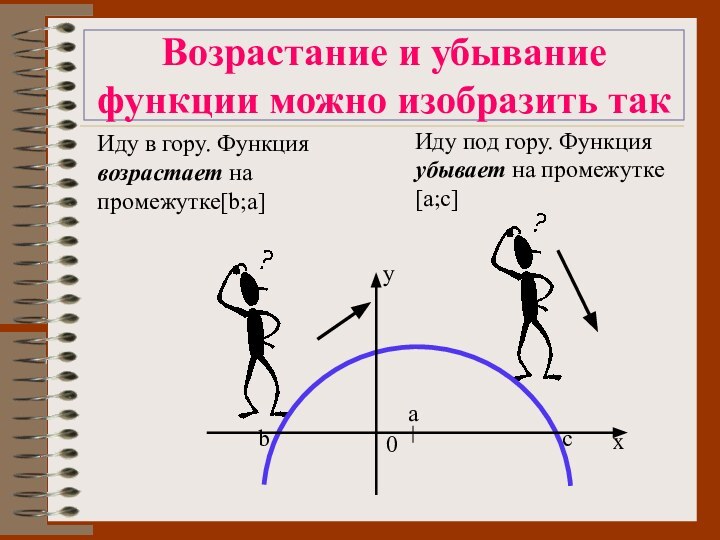
Возрастание и убывание функции можно изобразить так
Иду в
гору. Функция возрастает на промежутке[b;a]
Иду под гору. Функция убывает
на промежутке[a;с]
Слайд 7
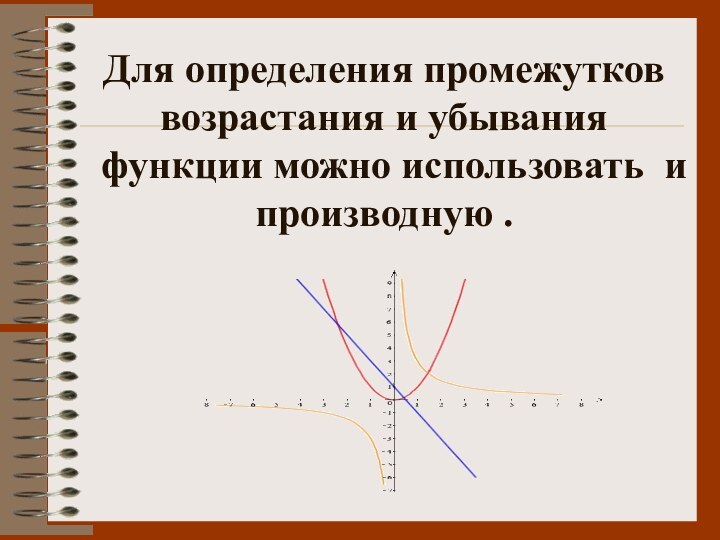
Для определения промежутков возрастания и убывания функции можно
использовать и производную .
Слайд 8
Теорема:
Если f(x) – непрерывна на промежутке и
имеет f´(x), то
а) если f´(x) > 0, то
f(x) – возрастает
б) если f´(x) < 0, то f(x) – убывает
в) если f´(x) = 0, то f(x) – постоянна
(константа)
Слайд 9
Алгоритм исследования функции на монотонность
Найти производную функции f
΄(х)
Найти стационарные (f ΄(х) = 0) и критические (f
΄(х) не существует) точки функции у= f(х)
Отметить стационарные и критические точки на числовой прямой
Определить знаки производной на получившихся промежутках
По знаку производной определить промежутки монотонности функции
(если f ΄(х) > 0 – функция возрастает; если f ΄(х) < 0
функция убывает; если f ΄(х) =0 – функция постоянна)
Слайд 10
Определения
Внутренние точки области определения функции, в которых производная
функции равна нулю, называются стационарными.
Внутренние точки области определения функции,
в которых функция непрерывна, но производная не существует, называются критическими
Слайд 11
Например: найти промежутки монотонности функции f(x) =
x³ - 6x² + 9x – 1
1) f´(x) =
3x² - 12x + 9
2) Найдем стационарные точки:
f´(x) = 0, 3x² - 12x + 9 = 0
x² - 4x + 3 = 0
x = 1 и х = 3
3)
4)
5) f ´(x) > 0, при x ϵ (-∞; 1) и (3; + ∞)
f ´(x) < 0, при х ϵ (1; 3)
Ответ: при x ϵ (-∞; 1) и (3; + ∞) функция возрастает, а при х ϵ (1; 3) - убывает
х
1
3
f ´(x)
f(x)
+
+
-
Слайд 12
Найти промежутки монотонности функции
у =
2х³ +3х² -100
у = х³ + 2х² +
6
у = 5х² + 15х - 1
у = 60 + 45х – 3х² - х³
у = - 3х + 6х² - 100
Слайд 13
Нахождение
точек экстремума
функции
Слайд 14
Определения
Точка хо называется точкой минимума функции у =
f(х), если у этой точки существует окрестность, для всех
точек которой выполняется неравенство
f(х) ≥ f(хо)
Точка хо называется точкой максимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство
f(х) ≤ f(хо)
Слайд 15
Определения
Значение функции в точке максимума обозначают уmax (но
на определенном участке вокруг точки максимума, а не на
всей области определения функции – это унаиб. )
Значение функции в точке минимума обозначают уmin (но это не унаим. функции на всей области определения)
Точки минимума и максимума называются точками экстремума
Слайд 16
Теорема
Пусть функция у = f(х) непрерывна на промежутке
Х и имеет внутри промежутка стационарную или критическую точку
х=х0. Тогда:
а) если у этой точки существует такая окрестность, в которой при х<х0 выполняется неравенство f΄(х) <0, а при х>х0 - неравенство f΄(х) >0, то
х0 – точка минимума функции у = f(х)
х0
- min
Слайд 17
х0
б) если у этой точки существует такая окрестность,
в которой при х 0,
а при х>х0 - неравенство f΄(х) <0, то
х0 – точка максимума функции у = f(х)
х0
- max
Слайд 18
х0
в) если у этой точки существует такая окрестность,
что в ней и слева и справа от точки
х0 знаки производной одинаковы, то в точке х0 экстремума нет (происходит изменение кривизны графика функции – это точка перегиба)
х0
х0
экстремума нет
Слайд 19
Алгоритм нахождения точек экстремума функции
Найти производную функции f
΄(х)
Найти стационарные и критические точки функции у = f(х)
Отметить
стационарные и критические точки на числовой прямой
Определить знаки производной на получившихся промежутках
Если f ′(х0) при переходе через точку меняет знак с «+» на «-», то эта точка – точка максимума. Если f ′(х0) при переходе через точку меняет знак с «-» на «+», то эта точка – точка минимума. Если f ′(Х0) не меняет знак, то в этой точке экстремума нет (это точка перегиба).
Слайд 20
Например: найти точки
экстремума функции
Решение. 1) у΄=12 х³ - 48х²
+ 48х =
= 12х(х²-4х+4) = 12х (х - 2)²
2) у΄=0 при х =0 и х =2 (стационарные точки)
3)
4)
5) Значит: х = 0 – точка минимума,
х = 2 - точка максимума.
х
0
2
-
-
+
f ´(x)
Слайд 21
Найдите точки экстремума функции и определите их характер
у
= 7 + 12х - х²
у = 3х³ +
2х² - 7
у = -2х³ + 21х² + 19
у = 3х² - х³
у = х + 4/х
Слайд 23
В тех случаях, когда речь идет о
построении графика незнакомой функции или
когда заранее
трудно представить вид графика,
используют следующий алгоритм:
Слайд 24
План построения графика функции с помощью производной
Найти область
определения функции и определить точки разрыва если они существуют
Выяснить
является ли функция четно или нечетной, проверить её на периодичность
Найти точки пересечения графика с осями координат, если это возможно
Найти стационарные и критические точки
Найти точки экстремума функции и промежутки монотонности
Определить промежутки вогнутости, выпуклости и точки перегиба графика функции
Найти координаты ещё нескольких точек (для большей точности)
Слайд 25
Как найти промежутки выпуклости, вогнутости и
точку перегиба графика функции
Промежутки выпуклости и вогнутости кривой можно
находить с помощью производной.
Теорема. (признак вогнутости и выпуклости)
Если вторая производная функции у=f(х) в данном промежутке положительна, то кривая вогнута в этом промежутке, а если отрицательна – выпукла в этом промежутке.
Слайд 26
Для нахождения интервалов выпуклости графика функции используют следующий
алгоритм:
Находят f΄(х), а затем f ΄΄(х)
Находят точки, в
которых f ΄΄(х) = 0
Отмечают полученные точки на числовой прямой и получают несколько промежутков области определения функции
Устанавливают знаки второй производной в каждом из полученных промежутков. Если f ΄΄(х) < 0, то на этом промежутке кривая выпукла; если
f ΄΄(х)>0 - вогнута
Слайд 27
0
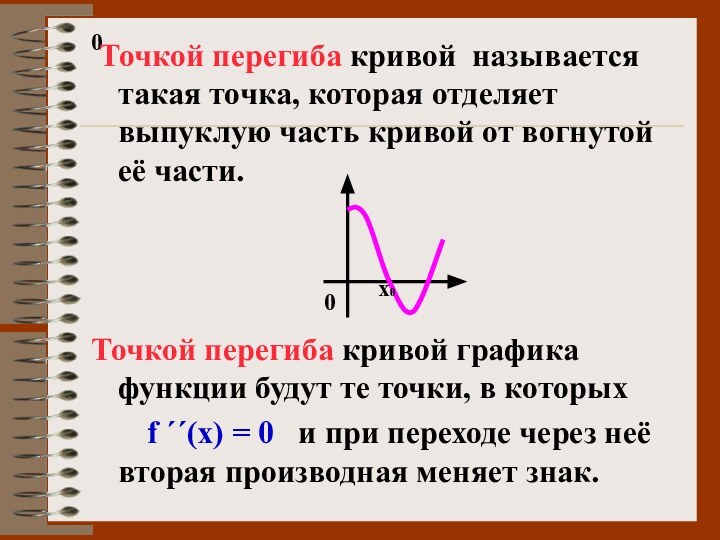
Точкой перегиба кривой называется такая точка, которая
отделяет выпуклую часть кривой от вогнутой её части.
Точкой перегиба
кривой графика функции будут те точки, в которых
f ΄΄(х) = 0 и при переходе через неё вторая производная меняет знак.
0
х0
Слайд 28
Найти интервалы выпуклости и точку перегиба
функции
Решение.
Найдем у΄(х) и у΄΄(х):
у΄(х) = 4х³-12х
=> у΄΄(х) = 12х²-12=12(х²-1)
Найдём стационарные точки второго порядка,
т.е. у΄΄(х)=0 => 12(х²-1)=0 => х²-1=0 => х²=1
х = ±1
Значит: при х ϵ (-∞; -1) и (1;+ ∞ ) функция вогнута, а при х ϵ (-1:1) – выпукла; точки перегиба х= ±1
1
-1
у΄΄(х)
+
+
-
Слайд 29
Например: исследовать функцию
у = 2х³+3х² -1 и
построить её график
Решение. D(у)= (-∞; +∞), четность не
определена
Найдем стационарные точки:
т.к. у΄=6х²+6х=6х(х+1) => 6х(х+1)=0
тогда х=0 и х=-1 стационарные точки
Найдем точки экстремума:
т.к.
и х=-1 – точка максимума
х= 0 – точка минимума
х
0
-1
f´(x)
+
+
-
f(x)
Слайд 30
Найдем промежутки монотонности:
при x ϵ (-∞; -1]
и [0; + ∞) - функция возрастает
при
x ϵ [-1; 0] - функция убывает
Найдем точки пересечения графика с осями координат:
если х=0, то у=-1 => (0;-1)
если у=0, то х= -1 => (-1; 0)
Слайд 31
Найдем ещё некоторые точки (контрольные, дополнительные):
т.к. х=-1
– точка максимума, то уmax=0 => (-1; 0) -точка
локального максимума
т.к. х= 0 – точка минимума, уmin=-1
=> (0;-1) -точка локального минимума
если х=1, то у=4 => (1;4)
если х=-2, то у=-5 => (-2;-5)
Удобнее все эти данные заполнять в виде таблицы.
Слайд 32
↓
Составим таблицу:
Найдем f ΄΄(х).
f΄΄(х) =(6х(х+1))΄=12х+6 = 6(2х+1)
f΄΄(х)=0 =>
6(2х+1)=0 => х = -0,5 - точка перегиба
т.к. при х=-1(левее х=-0,5) f΄΄(х) <0,
а при х=-0,1(правее х=-0,5) f΄΄(х) >0
Найдем её координаты: (-0,5; ? ), если это не трудно
Слайд 33
х
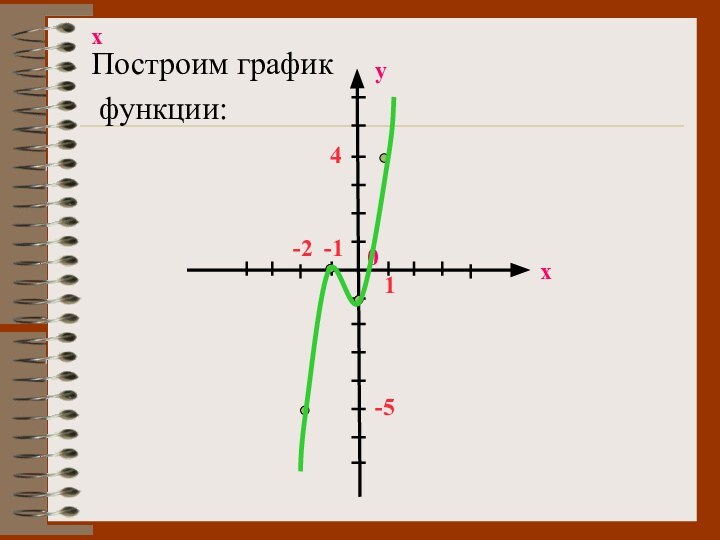
Построим график
функции:
х
у
0
-1
-2
4
1
-5
Слайд 34
Исследовать функцию и
построить её график
1) у =
3х² - х³
2) у = - 9х + х³
3) у = х³ - 3х² + 2
4) у = - х³ + 6х² - 5
5) у = 3х³ + х² - 8х – 7
6) у = (х)/(1+х²)
Слайд 35
Нахождение
наибольшего
и
наименьшего
значений
непрерывной
функции
на промежутке
Слайд 36
Теорема
Дифференцируемая на (а;b) и непрерывная на [a;b] функция
у=f(x) достигает своего наибольшего (наименьшего) значения на границе отрезка
[a;b] или в одной из точек экстремума на интервале (а;b).
Если функция удовлетворяет условиям теоремы и имеет единственную точку экстремума – точку максимума (минимума), то в ней достигается наибольшее (наименьшее) значение
Слайд 37
Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции
у=f(х) на отрезке [а;в]
1) Найти производную f ΄(х)
2)
Найти стационарные и критические точки функции и проверить принадлежат ли они
отрезку [а;в]
3) Вычислить значение функции у=f(х)
на концах отрезка, т.е в точках х=а и х=в
в стационарных и критических точках, принадлежащих [а;в]
4) Выбрать среди найденных значений наименьшее (это и будет Унаим.) и наибольшее (это и будет Унаиб.)
Слайд 38
Например: найти наименьшее и наибольшее значения функции
у=
х³ - 3х² - 45х + 1 на
отрезках а)[-4;6]
б) [-2;2]
а) 1) у΄= 3х² - 6х - 45
2) у΄= 0 => 3х² - 6х - 45 = 0|:3
х² - 2х - 15 = 0 =>
х1=-3 ϵ [-4;6] и х2= 5 ϵ [-4;6]
3) Найдём у(-4); у(6); у(-3); у(5):
Получим: у(-4)=69; у(6)=-161; у(-3)=82;
у(5)=-174.
Значит: Унаим = -174; Унаиб = 82.
Решение.
Слайд 39
Решение. б) на [-2;2]
1) у΄= 3х² - 6х – 45
2) у΄= 0 => 3х² - 6х - 45 = 0|:3
х² - 2х - 15 = 0 => х1=-3 ¢ [-2;2]
х2= 5 ¢ [-2;2]
3) Найдём у(-2); у(2):
Получили у(-2)= 71; у(2)=-93
Значит: Унаим = - 93; Унаиб = 71.
Слайд 40
Самостоятельно найдите
наименьшее и наибольшее
значения функции
у= х³ -
3х² - 45х + 1
на отрезке [0;6]
Ответ: Унаим. = -174 (достигается в точке х=5)
Унаиб. = 1 (достигается в точке х=0)
Слайд 41
Найдите наименьшее и наибольшее значения функции на заданном
промежутке.
1) у = х²-8х+19 на [-1;5]
2)
у = х³-9х²+24х-1 на [-2;3]
3) у = х+4/(х+1) на [-2;0]
4) у = х³-2х²+1 на [0,5;+∞)
5) у = 0,2х-х² на (-∞; 1]
Слайд 43
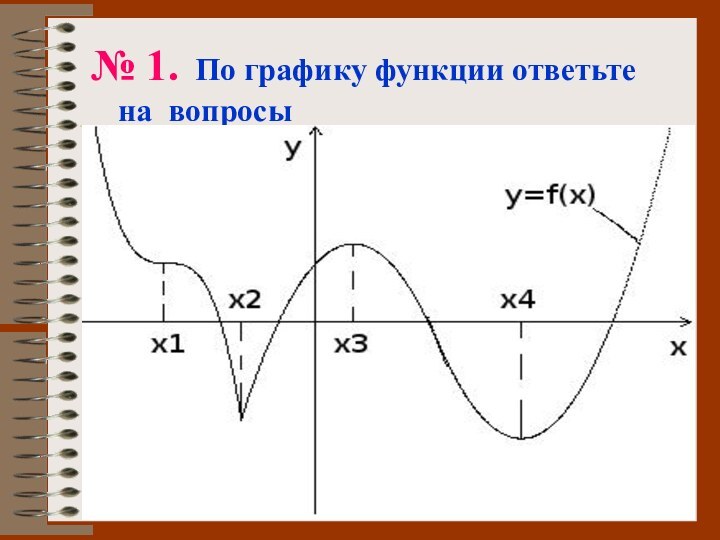
№ 1. По графику функции ответьте на вопросы
Слайд 44
1) Отметьте стационарные точки.
2) Что можно
сказать о производной в точке х1?
3) Назовите точки
экстремума.
4) Что можно сказать о производной на (−∞; х2)?
5) Укажите промежутки возрастания функции.
6) Отметьте критические точки
Слайд 45
Проверим ответы
1. (х1,х3,х4).
2. не существует.
3. (х2,х3,х4).
4. f′(х)
≤ 0.
5. [х2; х3]U [х4;+∞)функция возрастает.
6. х2
Слайд 46
№ 2. Постройте график непрерывной функции у =
f(х), определенной на [а;в], удовлетворяющей следующим условиям:
а) а=-1, в=4,
f΄(х)>0 при -1<х<4, f(1)=0, f(4)=3
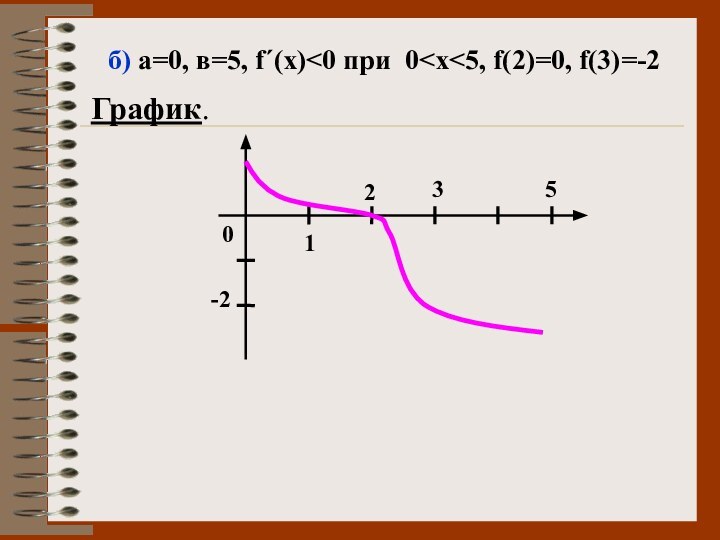
б) а=0, в=5, f΄(х)<0 при 0<х<5, f(2)=0, f(3)=-2
График.
а)
-1
1
1
3
4
Слайд 48
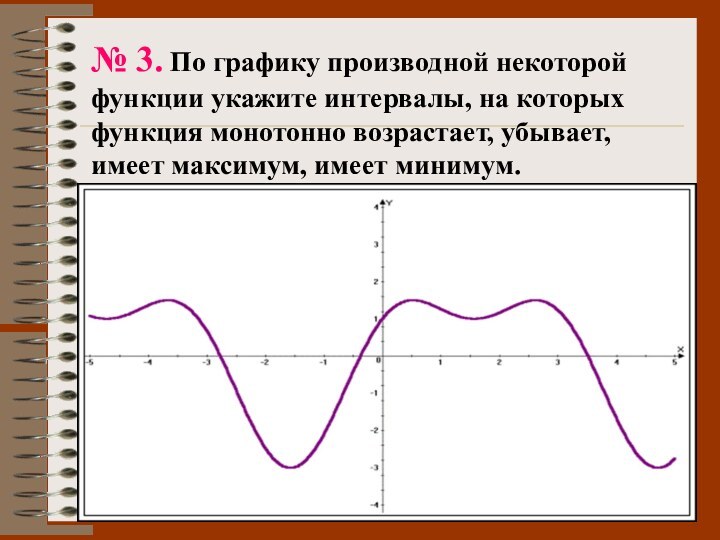
№ 3. По графику производной некоторой функции укажите
интервалы, на которых функция монотонно возрастает, убывает, имеет максимум,
имеет минимум.
Слайд 49
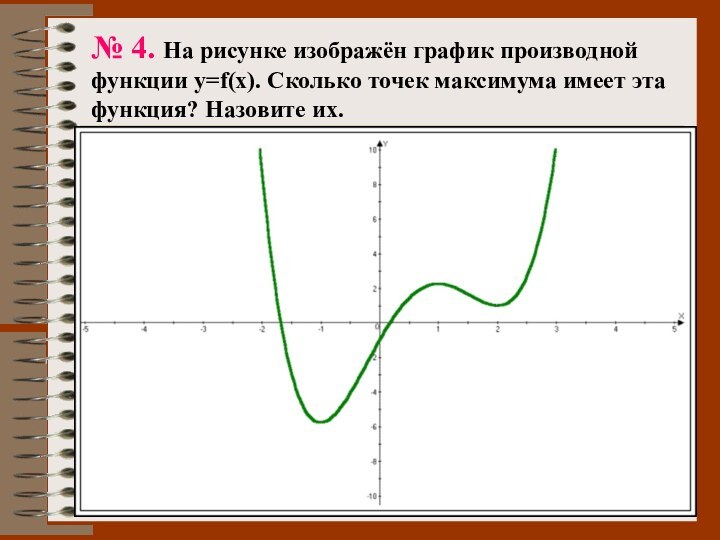
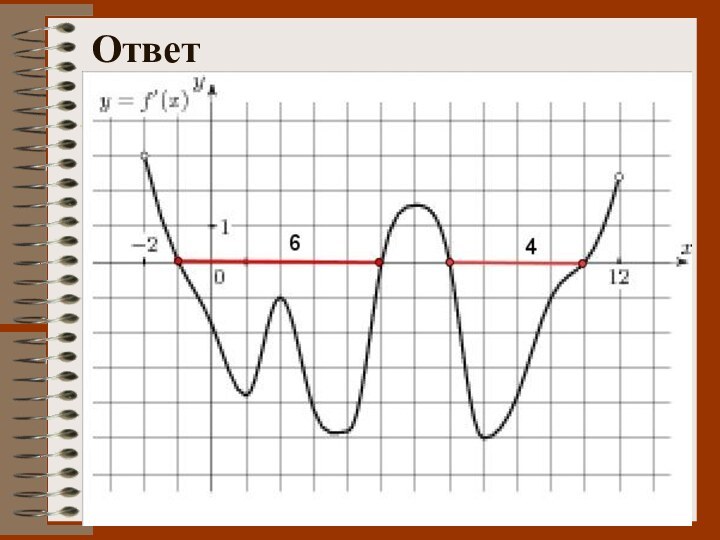
№ 4. На рисунке изображён график производной функции
y=f(x). Сколько точек максимума имеет эта функция? Назовите их.
Слайд 50
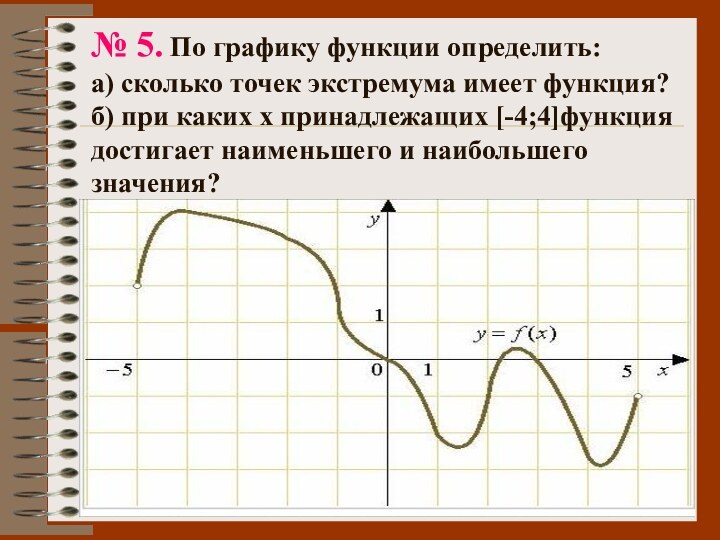
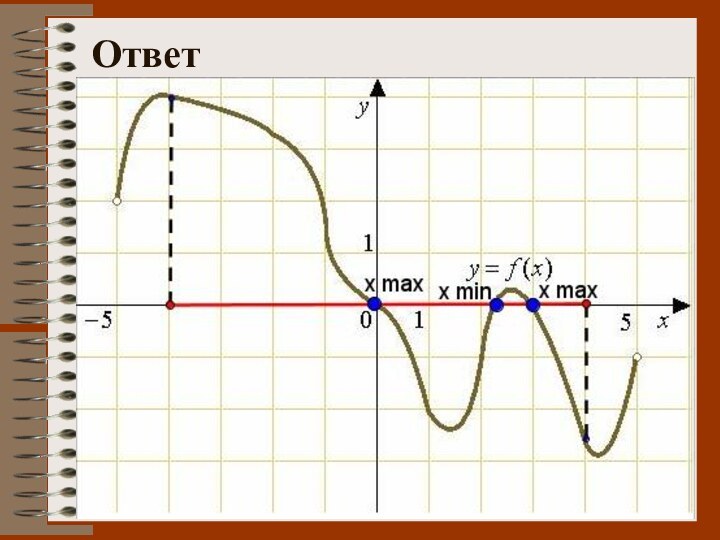
№ 5. По графику функции определить:
а) сколько
точек экстремума имеет функция? б) при каких х принадлежащих
[-4;4]функция достигает наименьшего и наибольшего значения?
Слайд 52
№ 6. Дан график производной некоторой функции.
Определить промежутки, на которых функция убывает?
Слайд 54
Верно или не верно №1
1. График
производной. Точки х=-1, х=1, х=2 являются точками максимума?
2.
Производная функции в точке хо равна 0, значит хо - критическая точка. Верно ли?
3. Производная функции не существует в точке хо, значит хо - критическая точка. Верно ли?
Слайд 55
4. Критическая точка является точкой экстремума. Верно ли?
5.
Точка экстремума является критической точкой. Верно ли?
6. Функция y(x)
непрерывна в точке x=4, причем y' (x)>0 на (1;4) и y'(x)<0 на (4;7). Точка x=4 является точкой минимума?
Слайд 56
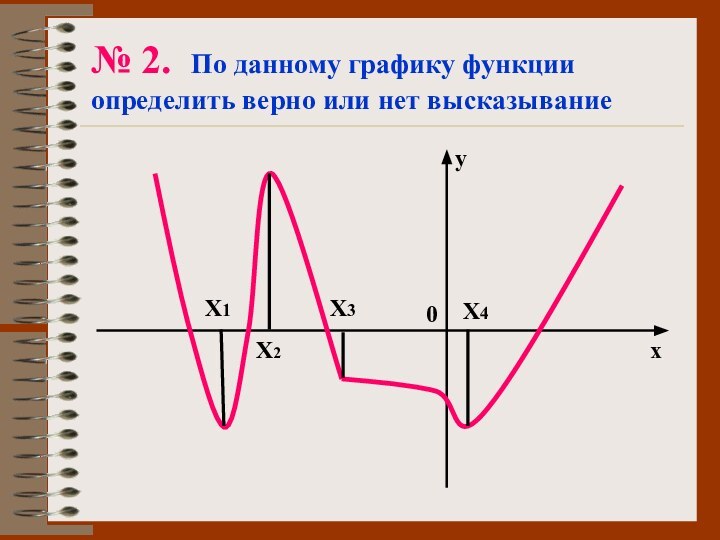
№ 2. По данному графику функции определить верно
или нет высказывание
0
х
у
Х1
Х2
Х3
Х4
Слайд 57
Да
Точка х1 – точка минимума.
Точка х1 – точка
перегиба.
В точках х2 и х4 касательная параллельна оси абсцисс
В
точке х3 производной не существует.
Точка х4 – точка экстремума
Точка х4 – точка минимума
Точка х4 – стационарная точка
Точка х3 – точка экстремума
Точка х2 – точка максимума
Да
Да
Да
Да
Да
Да
Да
Нет
Нет
























![Использование производной для исследования функции и построения графика функции (10 класс) Найдем промежутки монотонности: при x ϵ (-∞; -1] и [0; + ∞)](/img/tmb/13/1203483/dcd905b9d9adb58c46231fdcca7e166b-720x.jpg)




![Использование производной для исследования функции и построения графика функции (10 класс) ТеоремаДифференцируемая на (а;b) и непрерывная на [a;b] функция у=f(x) достигает своего наибольшего](/img/tmb/13/1203483/3136fc39896bca3c941432cdbb3057d8-720x.jpg)
![Использование производной для исследования функции и построения графика функции (10 класс) Алгоритм нахождения наибольшего и наименьшего значений непрерывной функции у=f(х) на отрезке [а;в]1)](/img/tmb/13/1203483/294d618e7f808c65559a83f12a9e7f71-720x.jpg)

![Использование производной для исследования функции и построения графика функции (10 класс) Решение. б) на [-2;2] 1) у΄= 3х² - 6х](/img/tmb/13/1203483/f5aa32e0a5532f23fdef1c9e8a04cef3-720x.jpg)




![Использование производной для исследования функции и построения графика функции (10 класс) № 2. Постройте график непрерывной функции у = f(х), определенной на [а;в],](/img/tmb/13/1203483/79c2c8fc7c0d68aa7df0dcac46d81204-720x.jpg)