обратную, уметь применять при решении квадратных уравнений
«Вся
математика – это, собственно, одно большое
уравнение для других наук»
Новалис
Девиз урока:
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть




















Девиз урока:
x² + px + q =0
Доказать:
х₁ + х₂ = -p,
х₁ ∙ х₂ = q
Теорема Виета
=
=
= -p
3. x₁ ∙ x₂ =
∙
=
=
=
, D = p² -4q.
=
=
= q
2. x₁+x₂=
+
=
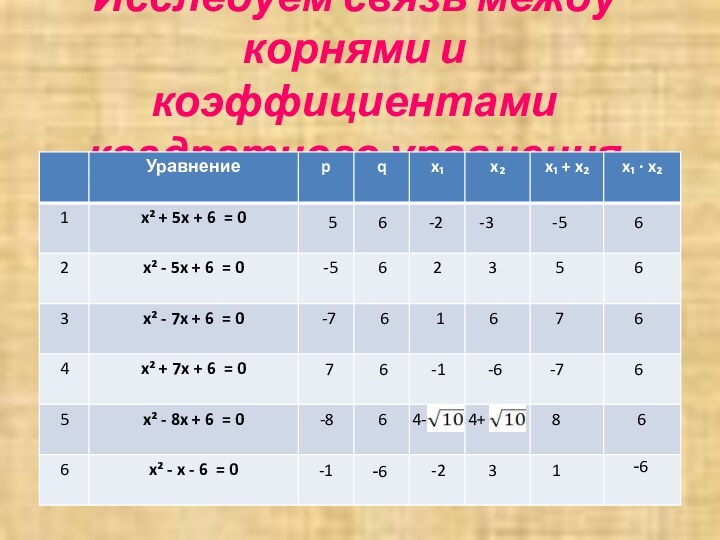
2. Для всех ли приведенных уравнений x₁+ x₂= -p
x₁· x₂= q
3. Сформулируйте теорему со словами «Если…, то…»
Задание 1. Выберите уравнение сумма корней которого равна -6, а произведение равно -11
х² - 6х + 11 = 0
х² + 6х - 11 = 0
х² + 6х + 11 = 0
х² - 11х - 6 = 0
х² + 11х - 6 = 0
1) p = -6, q = -5
2) p = 5, q = 6
3) p = 6, q = 5
4) p = -5, q = -6
5) p = 5, q = -6
6) p = -6, q = -5
х₁ + х ₂= -3, х₁ ∙ х₂ = -5
х₁ + х ₂= -5, х₁ ∙ х₂ = -3
х₁ + х ₂= 3, х₁ ∙ х₂ = -5
х₁ + х ₂= 5, х₁ ∙ х₂ = -3
№573
а) в) у доски
г) д) самостоятельно с последующей проверкой
:2
Для каждого уравнения попытайтесь подобрать два числа х₁ и х₂ так, чтобы выполнялись получившиеся равенства.
2. х² + 7х + 12 = 0
3. y² – 8y – 9 = 0
D > 0, p = -2, q = -8
x₁ + x₂ = 2
x₁ ∙ x₂ = -8
D > 0, p = 7, q = 12
x₁ + x₂ = -7
x₁ ∙ x₂ = 12
D > 0, p = -8, q = -9
y₁ + y₂ = 8
y₁ ∙ y₂ = -9
x₁ = -2
x₂ = 4
2 ∙ (-4)
-2 ∙ 4
1 ∙ (-8)
-1 ∙ 8
Проверьте, будут ли полученные числа корнями данного уравнения
x₁ = -3
x₂ = -4
y₁ = -1
y₂ = 9
Обратная теорема:
Если числа х₁, х₂ и p, q связаны равенствами
х₁ + х₂ = -p,
х₁ ∙ х₂ = q.
Теорема Виета
х₁ + х₂ = -p,
х₁ ∙ х₂ = q
Тогда х₁ и х₂ - корни уравнения
х² + px + q = 0.
Числа х₁ и х₂ являются корнями приведенного квадратного уравнения х² + px +q = 0 тогда и только тогда, когда
x₁ +х₂ = - p, x₁ ∙ x₂ = q
По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого:
Умножишь ты корни — и дробь уж готова?
В числителе с, в знаменателе а
А сумма корней тоже дроби равна.
Хоть с минусом дробь, что за беда!
В числителе в, в знаменателе а.