Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Алгебра Производные

Содержание

Структура изучения темыПриращение аргумента, приращение функцииОпределение производнойНахождение производной по определению Формулы дифференцированияУравнение касательной Геометрический смысл производнойМеханический смысл производной
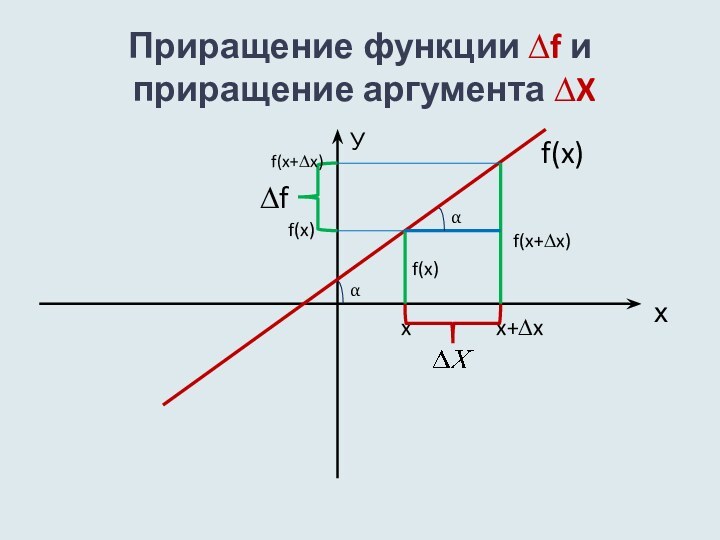
ПРОИЗВОДНАЯБессонова Т.Д.ВСОШ№7Г.Мурманск2008 Структура изучения темыПриращение аргумента, приращение функцииОпределение производнойНахождение производной по определению Формулы дифференцированияУравнение Приращение функции ∆f и приращение аргумента ∆XхУf(x)xx+∆xf(x)f(x)f(x+∆x)∆ff(x+∆x)αα Определение производнойПроизводной функции в данной точке называется предел отношения приращения функции в Происхождение терминов Алгоритм отыскания производной Пример нахождения производной по определению 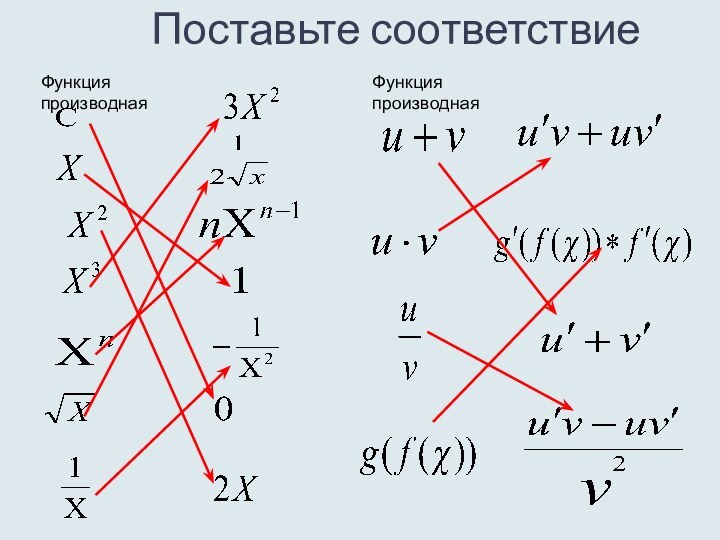Формулы дифференцированияФункция производнаяФункция производная Поставьте соответствиеФункция производнаяФункция Найти производную функции Самостоятельная работаf(x) = х4 - 4х3 + 6х2 _ Ответыf’(x) = 4x3 – 12x2 + 12xf’(x) = 35x4 - 27x2 + Критерии оценок«5» - без ошибок;«4» - 3 задания решены верно;«3» - 2 задания решены верно; 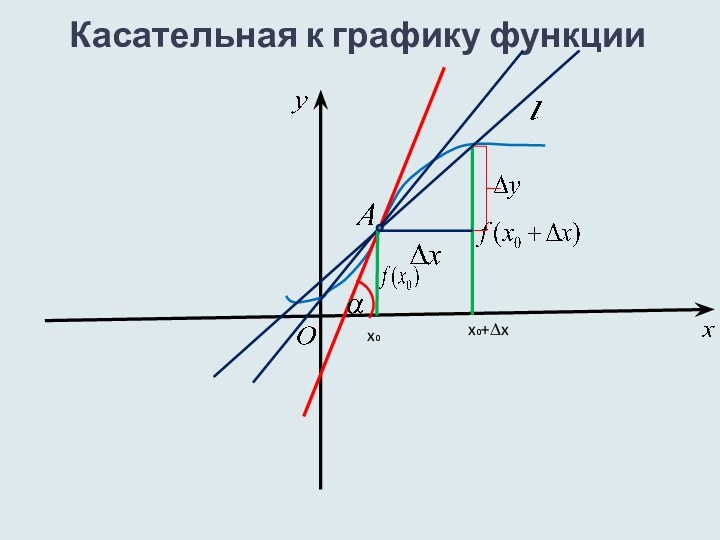Касательная к графику функцииx₀+∆xx₀ Геометрический смысл производнойГеометрический смысл производной состоит в том, что значение производной функции Решить задачуПрямая, проходящая через начало координат, касается графика функции На рисунке изображен график функции у = f(x) и касательная к нему Уравнение касательной Найти уравнение касательной к графику функции Механический смысл производной ЗадачаТочка движется прямолинейно по закону S(t) = 2 t ³ - 3 Задача №268Материальная точка движется прямолинейно по закону х(t)=t³- 4t²Найдите скорость и ускорение ЛитератураМордкович А.Г. Алгебра и начала анализа. 10-11 класс.: В двух частях. Ч.
Слайды презентации

Слайд 2 Структура изучения темы
Приращение аргумента, приращение функции
Определение производной
Нахождение производной

Структура изучения темыПриращение аргумента, приращение функцииОпределение производнойНахождение производной по определению Формулы

по определению
Формулы дифференцирования
Уравнение касательной
Геометрический смысл производной
Механический смысл

производной




Слайд 3 Приращение функции ∆f и приращение аргумента ∆X
х
У
f(x)
x
x+∆x
f(x)

f(x)
f(x+∆x)



∆f
f(x+∆x)

α

α

Приращение функции ∆f и приращение аргумента ∆XхУf(x)xx+∆xf(x)f(x)f(x+∆x)∆ff(x+∆x)αα

Слайд 4 Определение производной
Производной функции в данной точке называется предел

Определение производнойПроизводной функции в данной точке называется предел отношения приращения функции

отношения приращения функции в этой точке к приращению аргумента,

когда приращение аргумента стремится к нулю.

Слайд 5 Происхождение терминов

Происхождение терминов

Слайд 6 Алгоритм отыскания производной

Алгоритм отыскания производной

Слайд 7 Пример нахождения производной по определению

Пример нахождения производной по определению

Слайд 8 Формулы дифференцирования
Функция производная
Функция

Формулы дифференцированияФункция производнаяФункция производная

производная

Слайд 9 Поставьте соответствие
Функция

Поставьте соответствиеФункция производнаяФункция производная

производная
Функция

производная

Слайд 10 Найти производную функции Самостоятельная работа
f(x) = х4 - 4х3

Найти производную функции Самостоятельная работаf(x) = х4 - 4х3 + 6х2

+ 6х2 _ 7
f(x) = 7x5 – 9x3 +3x

-3,5

f(x) = (x3 _ 2x)(x2 + 3)

f(x) =

Слайд 11 Ответы
f’(x) = 4x3 – 12x2 + 12x
f’(x) =

Ответыf’(x) = 4x3 – 12x2 + 12xf’(x) = 35x4 - 27x2

35x4 - 27x2 + 3
f’(x) = 5x4 + 3x2

- 6

f’(x) =


Слайд 12 Критерии оценок
«5» - без ошибок;
«4» - 3 задания

Критерии оценок«5» - без ошибок;«4» - 3 задания решены верно;«3» - 2 задания решены верно;

решены верно;
«3» - 2 задания решены верно;

Слайд 13 Касательная к графику функции

x₀+∆x
x₀



Касательная к графику функцииx₀+∆xx₀

Слайд 14 Геометрический смысл производной
Геометрический смысл производной состоит в том,

Геометрический смысл производнойГеометрический смысл производной состоит в том, что значение производной

что значение производной функции y=f(x) в точке x0 равно

угловому коэффициенту касательной к графику функции в точке с абсциссой x0 :

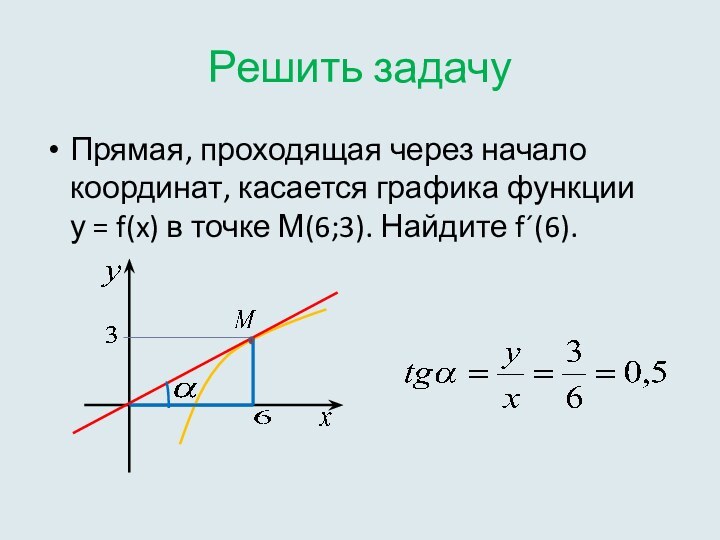
Слайд 15 Решить задачу
Прямая, проходящая через начало координат, касается графика

Решить задачуПрямая, проходящая через начало координат, касается графика функции

функции у = f(x)

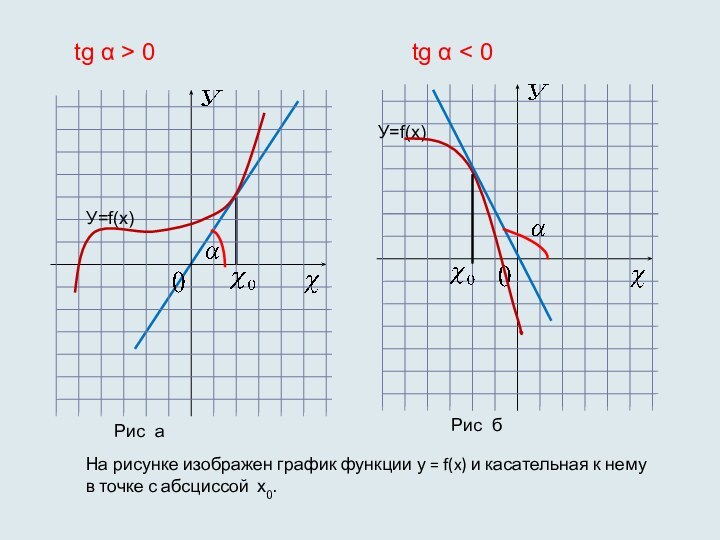
в точке М(6;3). Найдите f´(6).


Слайд 16 На рисунке изображен график функции у = f(x)

На рисунке изображен график функции у = f(x) и касательная к

и касательная к нему в точке с абсциссой х0.


Рис а

Рис б

tg α > 0

tg α < 0



Слайд 17 Уравнение касательной

Уравнение касательной

Слайд 18 Найти уравнение касательной к графику функции

Найти уравнение касательной к графику функции

Слайд 19 Механический смысл производной

Механический смысл производной

Слайд 20 Задача

Точка движется прямолинейно по закону S(t) = 2

ЗадачаТочка движется прямолинейно по закону S(t) = 2 t ³ -

t ³ - 3 t
Вычислите скорость

движения точки:
а) в момент времени t;
б) в момент времени t=2с.
Решение.

а)

б)


Слайд 21 Задача №268
Материальная точка движется прямолинейно по закону х(t)=t³-

Задача №268Материальная точка движется прямолинейно по закону х(t)=t³- 4t²Найдите скорость и

4t²
Найдите скорость и ускорение в момент времени t=5с.

(Перемещение измеряется в метрах)

  • Имя файла: algebra-proizvodnye.pptx
  • Количество просмотров: 216
  • Количество скачиваний: 0
- Предыдущая История 6 класс
Следующая - Растениеводство в нашем крае

Похожие презентации

Величина Величина 198
Путешествие в страну дробных чисел Путешествие в страну дробных чисел 189
Квадратичная функция Квадратичная функция 174
Преобразованиевыражений Преобразованиевыражений 165
Арифметические действия над целыми числами Арифметические действия над целыми числами 168
Формулы сокращенного умножения Формулы сокращенного умножения 162
Теория графов Теория графов 186
Применение определителей 2 и 3 порядка при решении задач №14 ЕГЭ по математике Применение определителей 2 и 3 порядка при решении задач №14 ЕГЭ по математике 77
Показательная функция и ее применение Показательная функция и ее применение 191
Графическое решение уравнений Графическое решение уравнений 157
Инфографика как способ повышения мотивации внеаудиторных самостоятельных работ Инфографика как способ повышения мотивации внеаудиторных самостоятельных работ 153
Презентация по алгебре на тему Геометрический смысл производной ( 11 класс) Презентация по алгебре на тему Геометрический смысл производной ( 11 класс) 229
Некоторые приёмы решения алгебраических уравнений высшей степени Некоторые приёмы решения алгебраических уравнений высшей степени 156
Квадратный трёхчлен Квадратный трёхчлен 201
Построение графика линейной функции вида у= kx + b Построение графика линейной функции вида у= kx + b 153
Сложение и вычитание смешанных чисел Сложение и вычитание смешанных чисел 141
Презентация по алгебре и началам анализа на теме Максимумы и минимумы. (11 класс) Презентация по алгебре и началам анализа на теме Максимумы и минимумы. (11 класс) 192
Тригонометрические функции углового аргумента Тригонометрические функции углового аргумента 167
Презентация по теме Метод рационализации Презентация по теме Метод рационализации 158
Презентация по математики на тему Решение задач с помощью уравнений Презентация по математики на тему Решение задач с помощью уравнений 182
Презентация Математика вокруг нас Презентация Математика вокруг нас 153
Презентация Подготовка к ОГЭ (9 класс) Презентация Подготовка к ОГЭ (9 класс) 168
Открытый урок по теме: Решение неравенств второй степени. Открытый урок по теме: Решение неравенств второй степени. 178
Пропорция Пропорция 162
НОД И НОК чисел НОД И НОК чисел 184
Графики тригонометрических функций Графики тригонометрических функций 175
Презентация к родительскому собранию 9 класс Презентация к родительскому собранию 9 класс 152
Презентация по математике Решение квадратных уравнений Презентация по математике Решение квадратных уравнений 159
Презентация по теме: Понятие о производной Презентация по теме: Понятие о производной 274
Презентация по алгебре на тему Квадратичная функция. Презентация по алгебре на тему Квадратичная функция. 153