Цели урока: рассмотреть линейную функцию, ее график и свойства, способ построения графика линейной функции Задачи урока: . Образовательные: введение понятия линейной функции; отработка навыка распознавания линейной функции по заданной формуле; отработка навыка вычисления значения функции по заданному значению аргумента, построения графика функции; выработать умение анализировать и находить правильное решение проблемных ситуаций. . Развивающие: развитие логического мышления, зрительной памяти, математически грамотной речи, сознательного восприятия материала. Воспитательные: воспитание познавательной активности, . чувства ответственности, культуры общения.
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему линейная функция и ее график
Содержание
- 4. Проверка готовности к уроку
- 5. Из историиРене ДекардГотфрид Лейбниц(1646-1716)(1596-1650)В первой половине XVII
- 6. Функцией называется зависимость одной
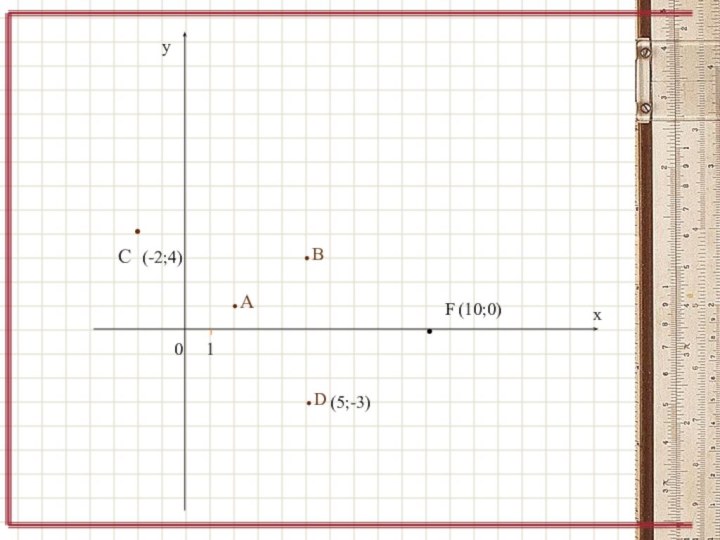
- 8. ух01.А.В.С(-2;4).D(5;-3).(10;0)F
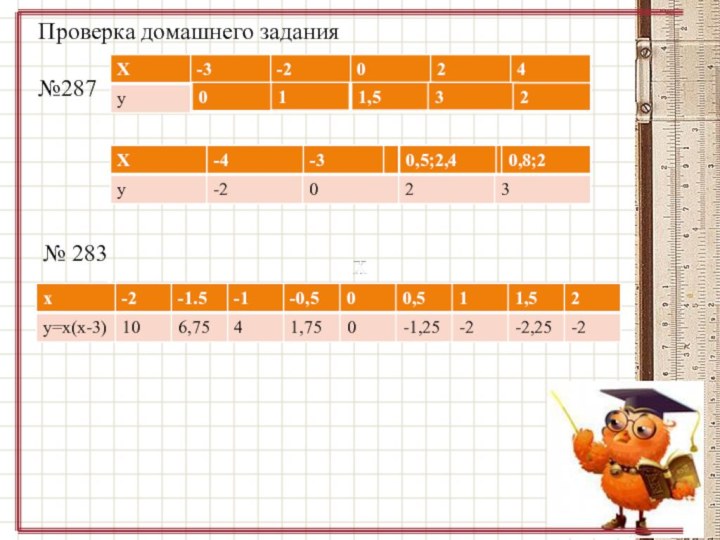
- 9. Проверка домашнего задания№287Х№ 283
- 10. Задача 1. Мама купила несколько конфет по
- 11. Задача 2. На шоссе расположены пункты
- 12. Какая формула выражает зависимость расстояния от времени
- 13. Итак, мы получили две формулы, выражающие совершенно
- 14. y = kx + b – линейная
- 15. Рассмотрим частные случаи.Если b = 0, то
- 16. Давайте выясним, является ли линейной функция, задаваемая
- 17. Найти уравнения линейных функций y=-x+0,2;
- 18. Является ли линейной функция y = (5x
- 21. 10.10.2015График функции0Пример 2Построить график функции а) у
- 22. Построить график линейной функции у = 2х
- 23. 10Построить график функции а) у = -31.
- 24. 10.10.2015График линейной функции0Вывод:Величина k определяет наклон графика
- 25. 10.10.2015График линейной функции0Вывод:Функция y = kx +
- 26. На каком рисунке коэффициент k в уравнении
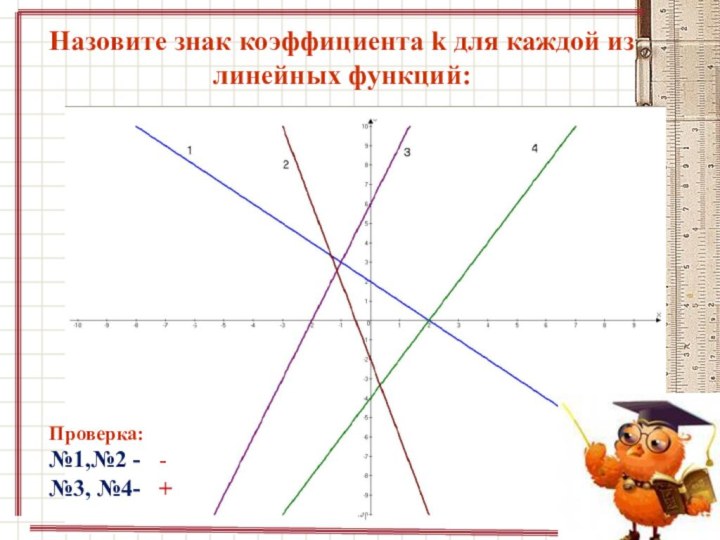
- 27. Назовите знак коэффициента k для каждой из линейных функций:Проверка:№1,№2 - -№3, №4- +
- 28. С помощью графика линейной функции у =
- 29. Заполните пропуски:• Прямой пропорциональностью называется функция вида
- 30. у=2х+1?Напишите функцию движения другой станции, так, чтобы эти корабли не столкнулись
- 31. Тема для проектной работыЛинейная зависимость в пословицах и поговорках.(Например, «Что посеешь, то пожнешь.»)
- 33. Скачать презентацию
- 34. Похожие презентации


























Слайд 2
Слайд 3
Тип урока — урок изучения нового материала.
Основные знания и умения
1. Знание определения линейной функции, прямой пропорциональности.
2. Иметь представление о графике линейной функции.
3. Уметь строить график линейной функции и работать с графиком.
4. Знать условия взаимного расположения графиков линейных функций.
5. Уметь решать задачи по теме как графически, так и аналитически.
Формы обучения
Фронтальная, индивидуальная, работа в парах
Оборудование: компьютер, мультимедийный проектор, карточки с заданиями, рабочая доска.
Слайд 5
Из истории
Рене Декард
Готфрид Лейбниц
(1646-1716)
(1596-1650)
В первой половине XVII века
в связи с развитием механики в математику проникают
идеи изменения и движения. В это время начинает складываться представление о функции как о зависимости одной переменной величины от другой.Французский математик Рене Декард (именем
которого и названа декардова система координат)
представлял себе функцию как зависимость
ординаты точки кривой от её абсциссы.
Термин «функция» (от латинского functio – исполнение, совершение) впервые ввёл немецкий математик Готфрид Лейбниц.
Слайд 6 Функцией называется зависимость одной переменной
от другой, при которой одному значению независимой переменной соответствует
единственное значение зависимой переменной.Область определения функции - все значения, которые может принимать независимая переменная - Х – аргумент, абсцисса точки
Актуализация знаний
Область значений функции - все значения, которые может принимать зависимая переменная – У – функция, ордината точки
Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты- соответствующим значениям функции.
Слайд 10
Задача 1.
Мама купила несколько конфет по цене
5 рублей за конфету и одну шоколадку по цене
65 рублей. Сколько она заплатила за всю покупку?Составьте выражение, с помощью которого можно подсчитать стоимость покупки.
n - рублей стоит вся покупка
d – количество конфет
Как вы думаете, от чего зависит стоимость покупки?
n=5d+65
От числа покупаемых конфет.
Слайд 11
Задача 2.
На шоссе расположены пункты А
и В, удаленные друг от друга на 20 км.
Мотоциклист
выехал из пункта В в направлении, противоположном А, со скоростью 50 км/ч. На каком расстоянии s (км) от пункта А будет мотоциклист через t часов?От чего зависит расстояние от пункта А до мотоциклиста, если скорость и расстояние АВ постоянны? 50км/ч
А. . В
20км
От времени. Чем дольше едет мотоциклист, тем большее расстояние он проедет от пункта А.
Слайд 12 Какая формула выражает зависимость расстояния от времени движения?
Давайте вспомним общую формулу, знакомую вам из курса физики
s = vt.Посмотрите на таблицу. Давайте разберемся, как получены значения расстояния.
В момент начала движения (t = 0) мотоциклист находился в пункте В, значит, s = 20 км. За 1 ч он отъехал от пункта В на 50 км, следовательно, расстояние s от пункта А до мотоциклиста s = 20 + 50 = 70 (км). За три часа мотоциклист отъехал от пункта В на расстояние, равное 150 км (используем формулу s=vt). Значит, расстояние от пункта А до мотоциклиста составит s = 20 + 150 = 170 (км).
Попробуйте записать формулу, выражающую зависимость расстояния от времени движения.
s = 50t + 20, где t > 0.
Обратите внимание на то, что полученная формула позволяет найти s для любого момента времени.
Слайд 13 Итак, мы получили две формулы, выражающие совершенно различные
факты и явления, но имеющие одинаковую структуру:
n = 5d + 65s = 50t + 20
Общий вид формулы: y = kx + b,
где k и b – некоторые числа, x – переменная величина.
Можно предположить, что эти факты и явления описываются одной и той же формулой. Функция, с которой мы столкнулись в обеих задачах, называется линейной.
Слайд 14
y = kx + b – линейная функция
х
– аргумент (независимая переменная)
у – функция (зависимая переменная)
k, b
– числа, коэффициенты), к ≠ 0
Слайд 15
Рассмотрим частные случаи.
Если b = 0, то формула
y = kx + b принимает вид
y = kx (k <> 0)этой формулой задается прямая пропорциональность.
Таким образом, прямая пропорциональность является частным случаем линейной функции.
Если k = 0, то формула y = kx + b принимает вид y = b
Функция, задаваемая этой формулой, является линейной. Она принимает одно и то же значение при любом х.
Слайд 16 Давайте выясним, является ли линейной функция, задаваемая следующими
формулами
1) y = 2x – 3
2) y = -
x + 53) y = 8x
4) y =7 – 9x
5) y = x/2 + 1
6) y = 2/(x + 1)
7) y = x 2 – 3
8) y =5
Обратите внимание на то, что функции
y = 8x и y =5 являются линейными (это частные случаи линейной функции).
?
Слайд 17
Найти уравнения линейных функций
y=-x+0,2;
y=12,4x-5,7 ;
y=-9x-18; y=5,04x;y=-5,04x; y=126,35+8,75x;
y=x-0,2; y=x:8;
y=0,005x; y=133,133133x; y=3-10, 01x; y=2:x;
y=-0,0049; y=х:62.
Слайд 18
Является ли линейной функция
y = (5x –1)
+ (-8x +9)?
Что бы ответить на этот вопрос
нужно упростить правую часть выражения.y = (5x –1) + (-8x +9)
у = 5x - 1 - 8x + 9
y = -3x + 8.
Ответ: функция линейная.
Iвар. y = 4(x – 3) + (x + 2)
II вар. у = 7(8 – x) + (x – 10)
Выполните еще два аналогичных задания
у = 5х-10
у = -6х+46
Слайд 19
Задать формулой функцию, график
которой параллелен прямой у = -8х + 11
и проходит через начало координат
у = -8х + 1
у = -8х
у = 8х
у = 11х
Задание
Слайд 20 у
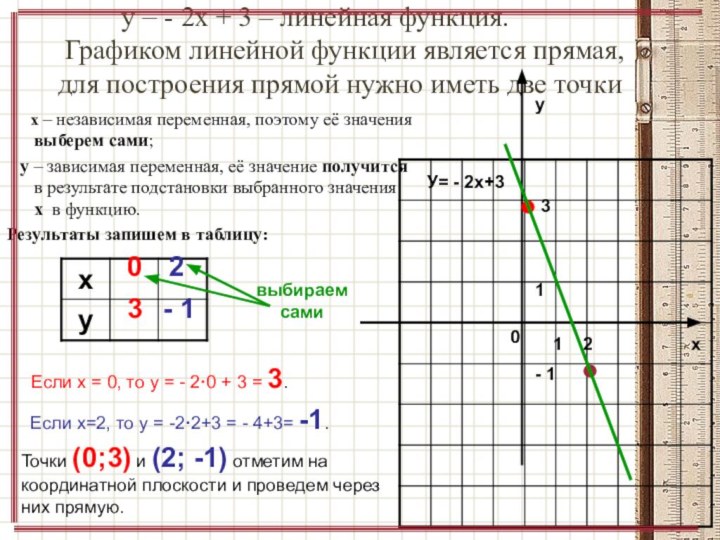
= - 2х + 3 – линейная функция.
Графиком линейной функции является прямая, для построения прямой нужно иметь две точки х – независимая переменная, поэтому её значения выберем сами;
у – зависимая переменная, её значение получится в результате подстановки выбранного значения х в функцию.
Результаты запишем в таблицу:
0
2
Если х = 0, то у = - 2·0 + 3 = 3.
3
Если х=2, то у = -2·2+3 = - 4+3= -1.
- 1
Точки (0;3) и (2; -1) отметим на координатной плоскости и проведем через них прямую.
х
у
0
1
1
У= - 2х+3
3
2
- 1
выбираем
сами
Слайд 21
10.10.2015
График функции
0
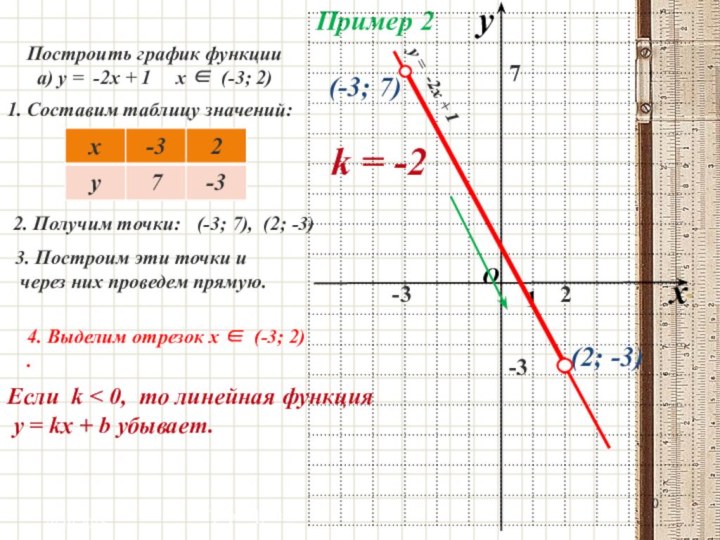
Пример 2
Построить график функции
а) у =
-2х + 1 х (-3; 2)
1.
Составим таблицу значений:2. Получим точки:
(-3; 7), (2; -3)
3. Построим эти точки и
через них проведем прямую.
(-3; 7)
(2; -3)
4. Выделим отрезок х (-3; 2) .
Если k < 0, то линейная функция
у = kx + b убывает.
k = -2
у = -2х + 1
Слайд 22
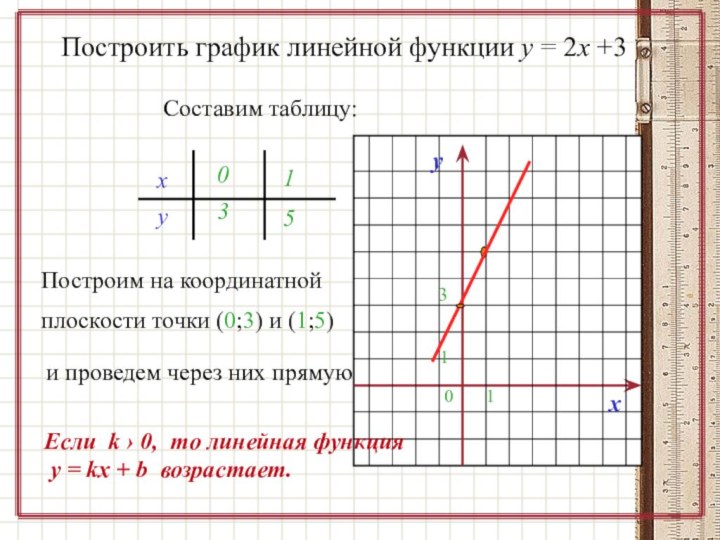
Построить график линейной функции у = 2х +3
Составим
таблицу:
х
у
03
1
5
Построим на координатной плоскости точки (0;3) и (1;5)
и
проведем через них прямуюЕсли k › 0, то линейная функция
у = kx + b возрастает.
Слайд 23
10
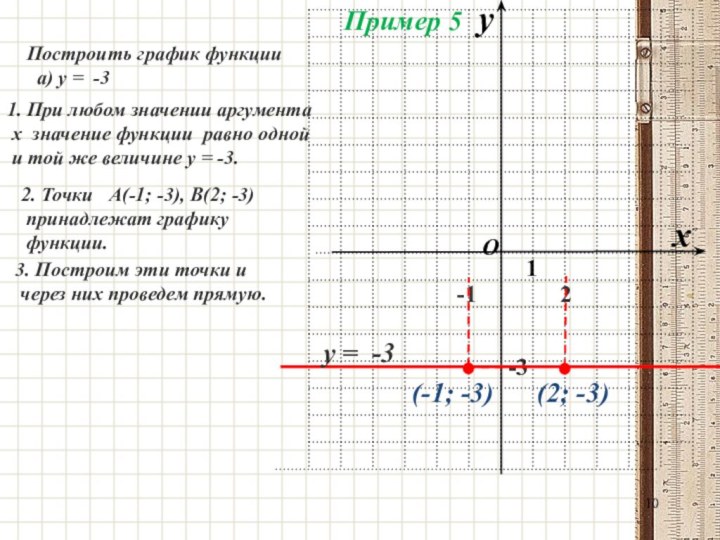
Построить график функции
а) у = -3
1. При
любом значении аргумента
х значение функции равно одной
и той же величине у = -3.
2. Точки А(-1; -3), В(2; -3)
принадлежат графику
функции.
3. Построим эти точки и
через них проведем прямую.
(-1; -3)
(2; -3)
у = -3
Пример 5
Слайд 24
10.10.2015
График линейной функции
0
Вывод:
Величина k определяет наклон графика
функции
y = kx + в
Если k
< 0, то линейная функция у = kx + b убывает.
Если k > 0, то линейная функция у = kx + b возрастает.
Если k = 0, то график линейной функции у = kx + b параллелен оси абсцисс (или совпадает с ней).
Слайд 25
10.10.2015
График линейной функции
0
Вывод:
Функция y = kx + m
называется возрастающей, если
большему значению аргумента соответствует
большее значение
функции (двигаясь по графику функции, мы поднимаемся вверх).
Функция y = kx + m называется убывающей, если
большему значению аргумента соответствует
меньшее значение функции (двигаясь по графику
функции, мы опускаемся вниз).
Слайд 26 На каком рисунке коэффициент k в уравнении линейной
функции отрицателен?
1
2 34 5
х
у
х
у
х
у
х
у
х
у
Слайд 28 С помощью графика линейной функции у = 2х
- 6 ответить на вопросы:
а) при каком значении
х будет у = 0 ? б) при каких значениях х будет у 0 ?
в) при каких значениях х будет у 0 ?
а) у = 0 при х = 3
б) у 0 при х 3
Если х 3 , то прямая расположена выше оси х, значит, ординаты соответствующих точек прямой положительны
в) у 0 при х 3
Если х 3, то прямая расположена ниже оси х, значит, ординаты соответствующих точек прямой отрицательны
Слайд 29
Заполните пропуски:
• Прямой пропорциональностью называется функция вида у=kx,
где х – независимая переменная, k – коэффициент, число.
•
Линейной функцией называется функция вида y=kx+b, где k и b - некоторые числа.• График линейной функции представляет собой прямую.
• Чтобы построить график линейной функции, необходимо:
1)выбрать значения независимой переменной x;
2)найти значение зависимой переменной у от выбранных значений x;
3)отметить найденные точки на координатной плоскости;
4)через построенные точки провести прямую.





























