понятия теории вероятностей.
Случайные величины.
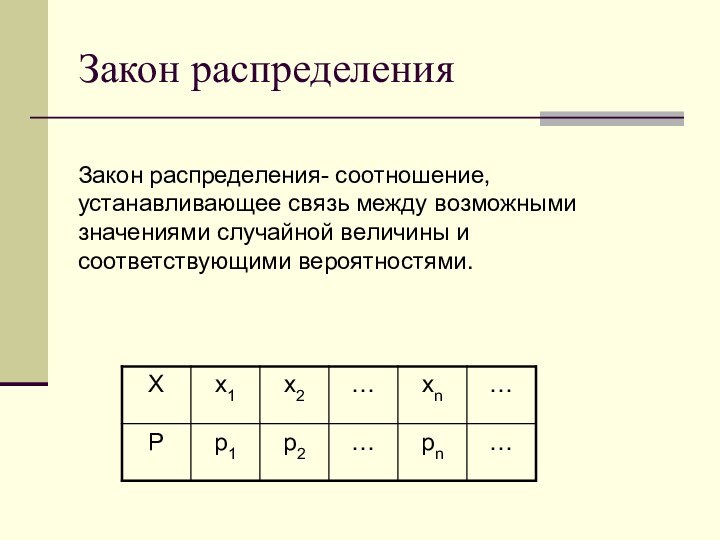
Закон распределения.
Пример.
Теория вероятностей в современном мире.
Химия
Химия &Химия & математика. Применение в статистике.
ФизикаФизика & Физика & математика.
Применение в астрономии.
Применение в сельском хозяйстве.
Применение в медицине.
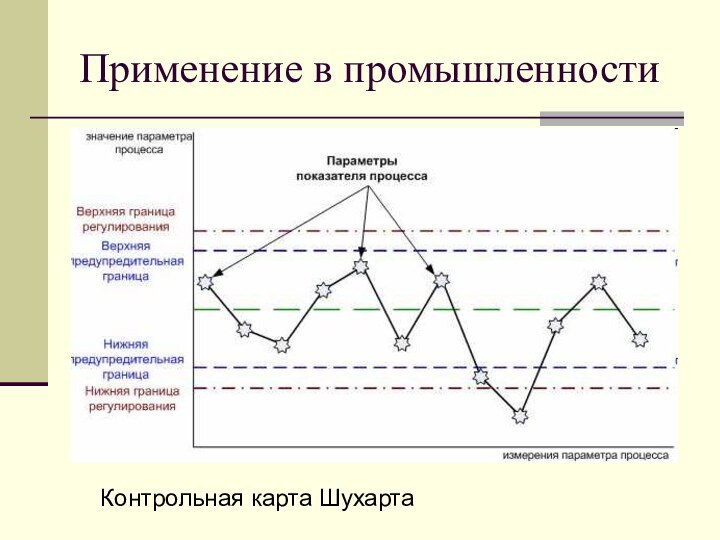
Применение в промышленности.
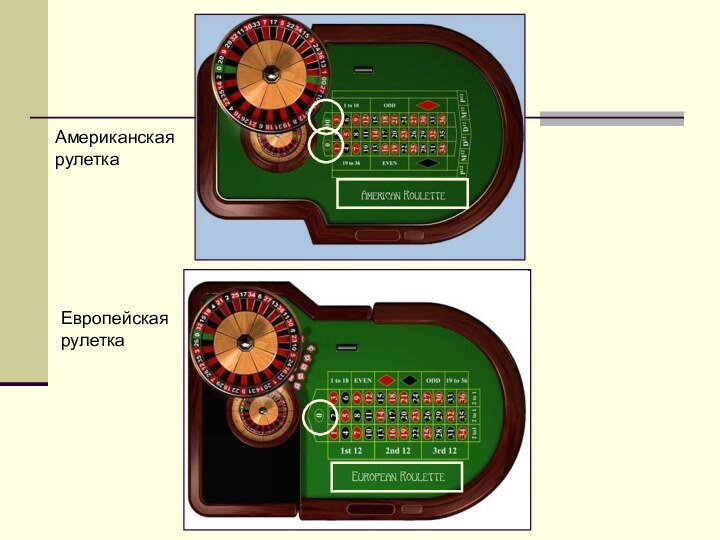
Применение в азартных играх (рулетка).
Применение в логических играх.
Список использованной литературы и сайтов.