первой квалификационной категории МОУ лицей № 176 Ткаченко Зоя
ВасильевнаАвтор:
Научный руководитель:
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


























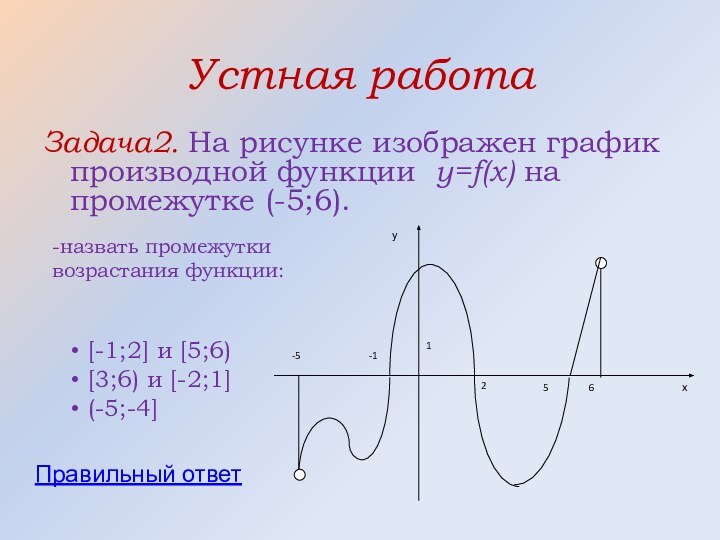
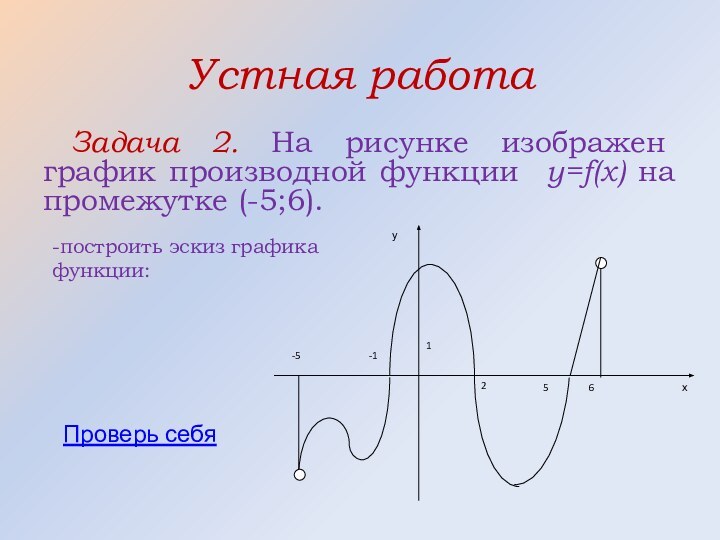
![Построение графиков с помощью производной Правильный ответ[-1;2] и [5;6)](/img/tmb/12/1134241/5678ed84089fc76c448202cfe05a63e7-720x.jpg)
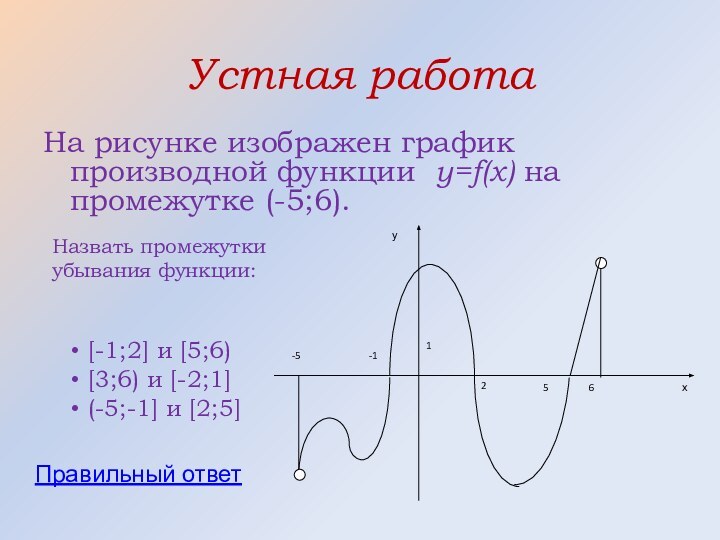
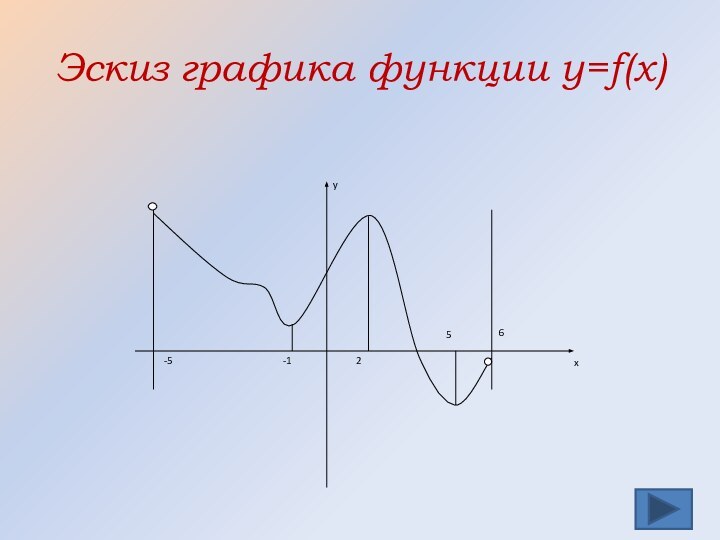
![Построение графиков с помощью производной Правильный ответ(-5;-1] и [2;5]](/img/tmb/12/1134241/8747e25476ebcfeb824207308d2c7154-720x.jpg)






















Автор:
Научный руководитель:
Вводная беседа
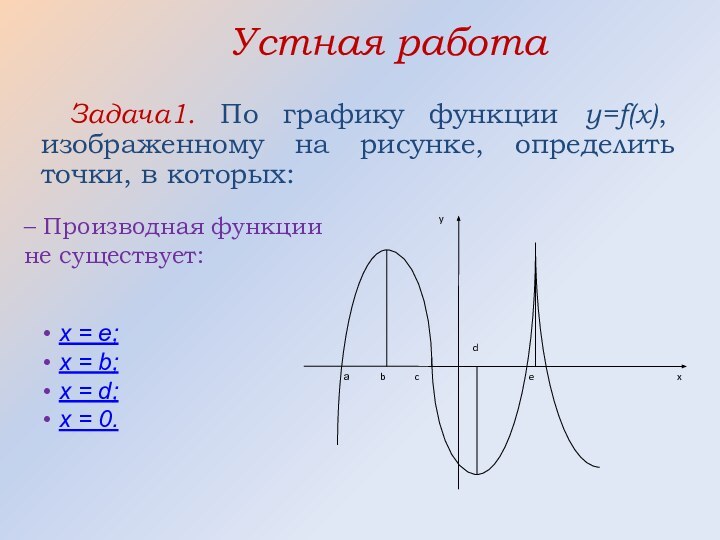
x = b, x = d;
x = c, x = a;
x = b, x = e, x = d;
x = e.
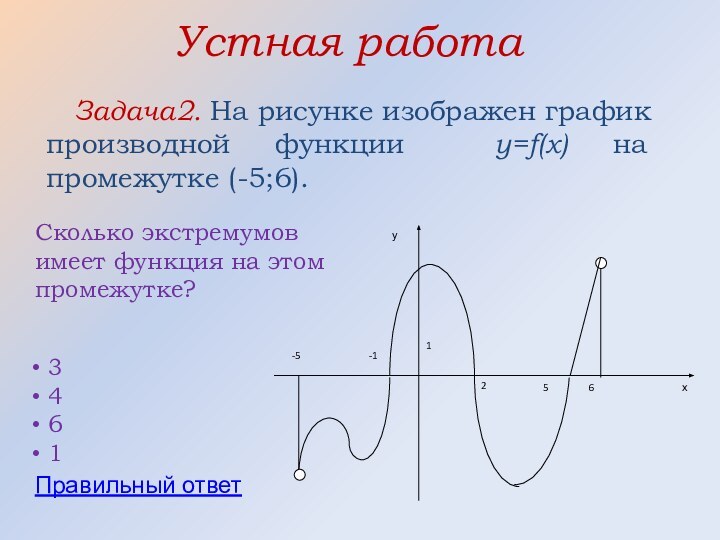
3
4
6
1
Правильный ответ
Правильный ответ
Правильный ответ
Уровни
.
Назад
.
Назад
.
Назад
График
Ответы:
Дополнительное задание:
Посмотрите в Посмотрите в MathCADПосмотрите в MathCAD(е).
Дополнительное задание:
Дополнительное задание:
Ответ
Посмотрите в Посмотрите в MathCADПосмотрите в MathCAD(е).
Ход урока
Далее
Далее
Методы математического анализа позволяют строить достаточно точный график заданной функции, если только удается хорошо изучить свойства этой функции.
Историческая справка
Ход урока
Далее
Рефлексия
Ответив на вопросы, оцените свои умения.