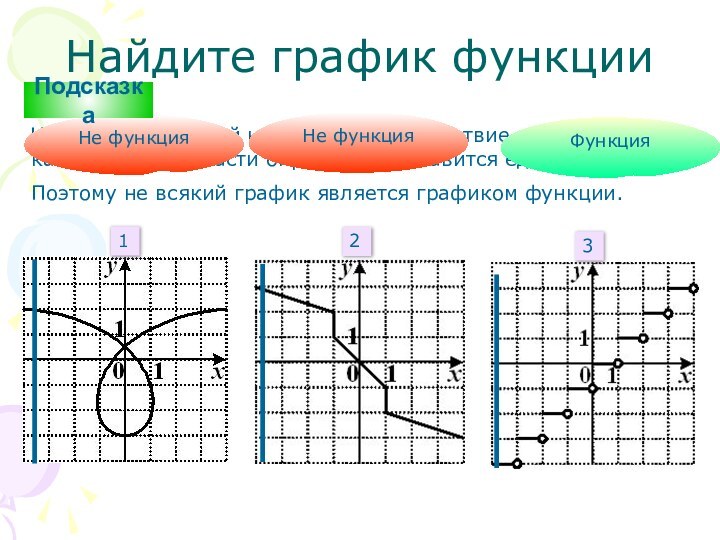
каждому х из области определения ставится единственное у.
Поэтому не
всякий график является графиком функции.1
2
3
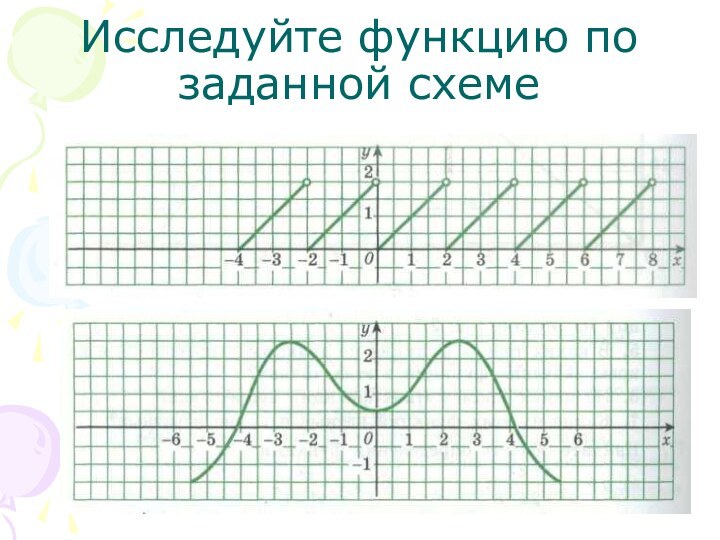
Не функция
Функция
Не функция
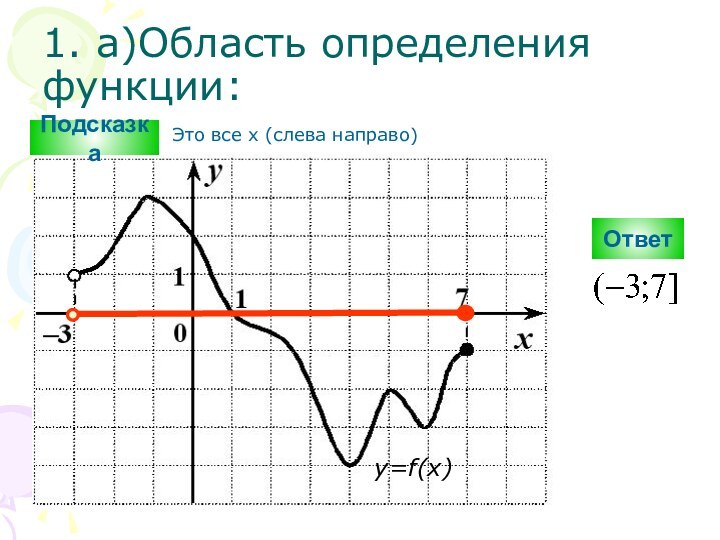
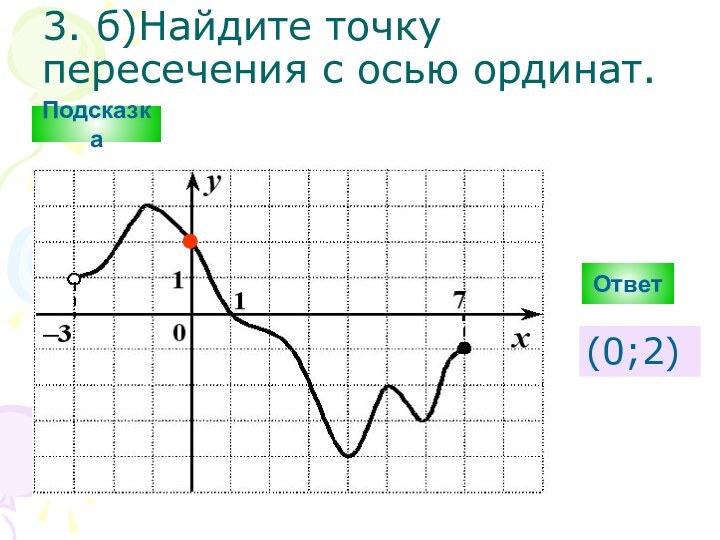
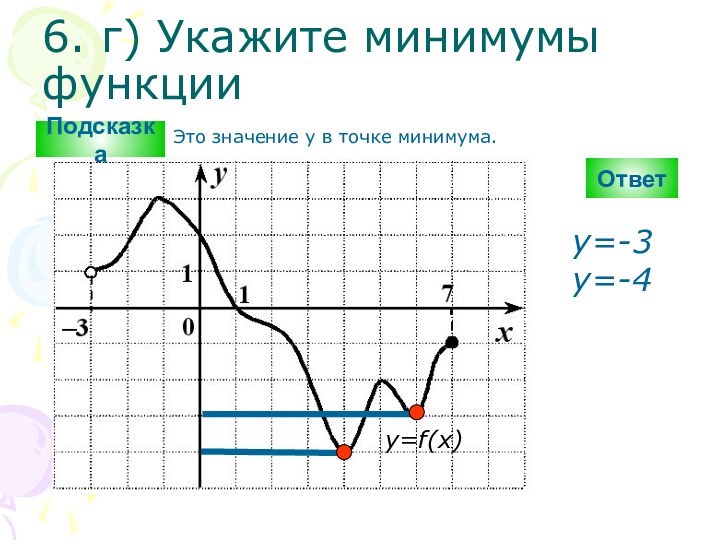
Подсказка
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



1
2
3
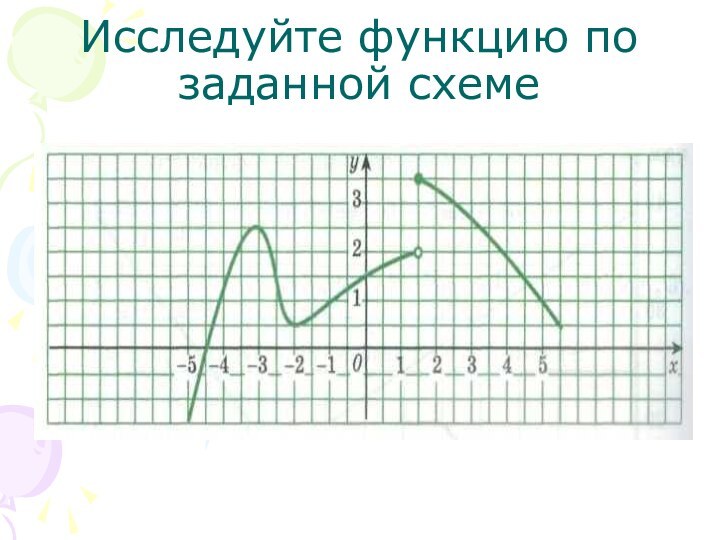
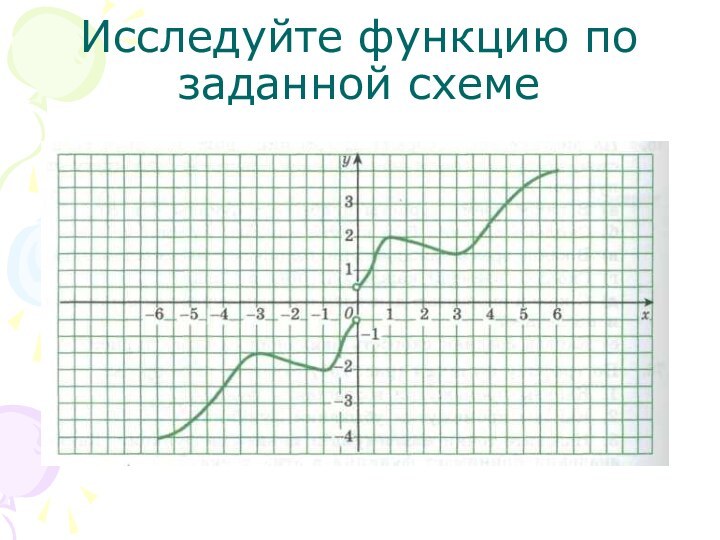
Не функция
Функция
Не функция
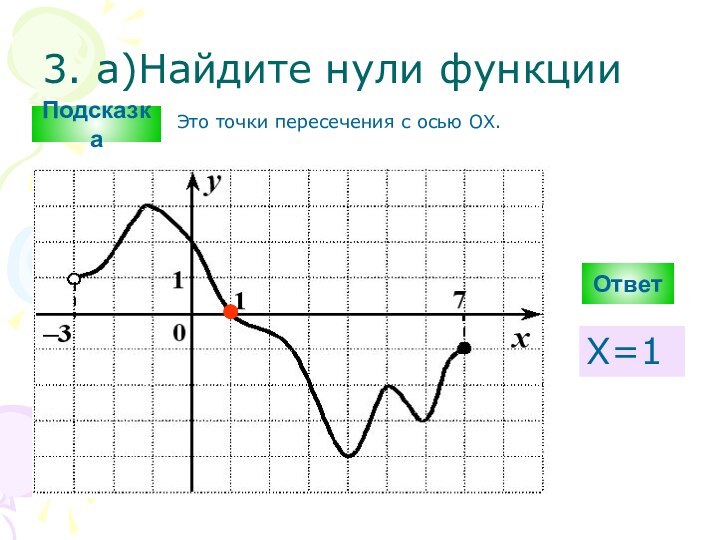
Подсказка
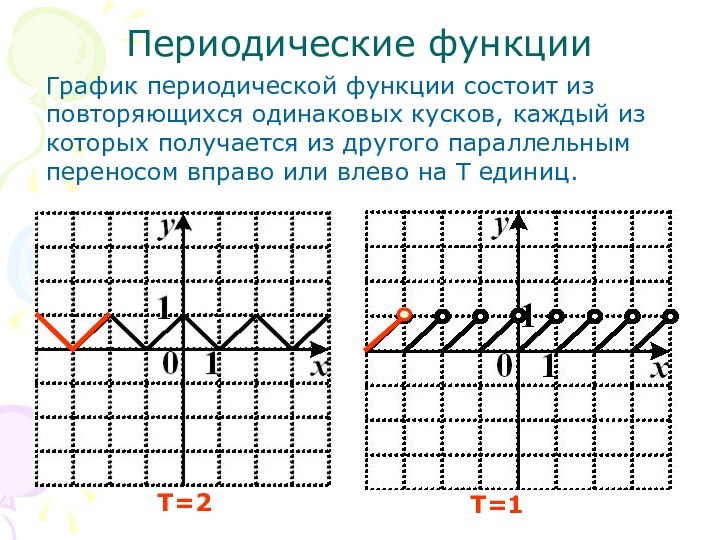
Т=2
Т=1
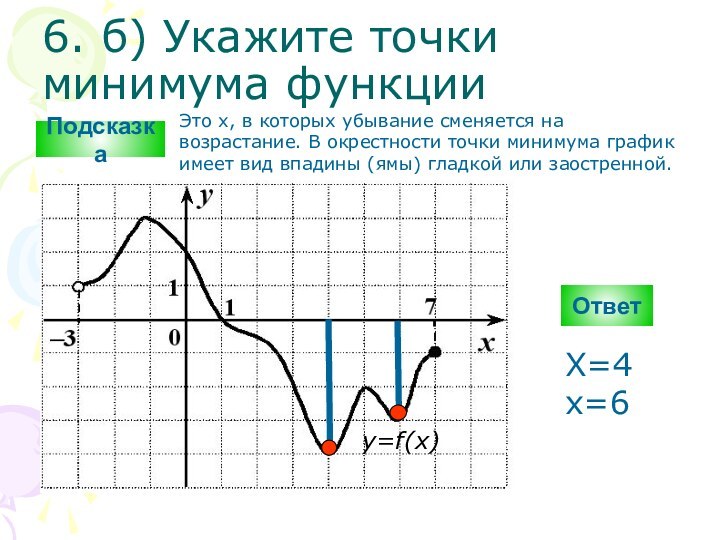
X=4 x=6