Презентация на тему по геометрии на тему Прямые и плоскости в пространстве

стены.
С точки зрения геометрии плоскость следует представлять как простирающуюся

неограниченно во все стороны.

Плоскость изображается:

В виде параллелограмма

В виде овала(облачка)

1. Понятие плоскости.

прямой, можно провести плоскость, и притом только одну.
Если две

точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

А

В

А

В

С

а

А

α

2. Аксиомы стереометрии.

проходит плоскость, и притом только одна.
Через две пересекающиеся прямые

проходит плоскость, и притом только одна.

О

а

в

а

А

3. Следствия из аксиом стереометрии.

общих
точек.
a
5. Параллельность прямой и плоскости.

плоскости, то линия пересечения плоскостей параллельна данной прямой.
Если одна

из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

a

a

b

Свойства параллельности прямой и плоскости.

6. Параллельность плоскостей.

плоскости соответственно параллельны двум прямым другой плоскости, то эти

плоскости параллельны.
Дано: α; β; a b=M; a a1;b b1; a β; b β
Доказать: β α
Доказательство:
Допустим, что плоскости α и β не параллельны. Тогда они пересекаются по некоторой прямой с. Мы получили, что плоскость α проходит через прямую а, параллельную плоскости β , и пересекает плоскость β по прямой с. Отсюда следует, что прямые а с. Но плоскость α проходит также через прямую b, параллельную плоскости β. Поэтому b c. Таким образом, через точку М проходит две прямые а и b, параллельные прямой с. Но это невозможно, т.к. по теореме о параллельных прямых через точку М проходит только одна прямая, параллельная прямой с. Значит, наше предположение неверно, => α β.

a1

b1

а

b

M

Признак параллельности плоскостей.

их пересечения параллельны.
Отрезки параллельных прямых, заключенные между параллельными плоскостями,

равны.

a

b

Свойства параллельных плоскостей.

к любой прямой, лежащей в этой плоскости.
А

7. Перпендикулярность прямой

и плоскости.

1. Если одна из двух параллельных прямых перпендикулярна

к плоскости, то и другая прямая перпендикулярна к этой плоскости.

Дано: α
а а1; а α
Доказать: а1 α
Доказательство:
Проведем произвольную прямую x в плоскости α. Т.к. прямая а α, то а x = > а1 х (по лемме о перпендикулярности двух параллельных прямых к третьей) = > а1 перпендикулярна любой прямой в плоскости α. = > а1 α .

a

a1

x

Свойства
перпендикулярности прямой и плоскости.

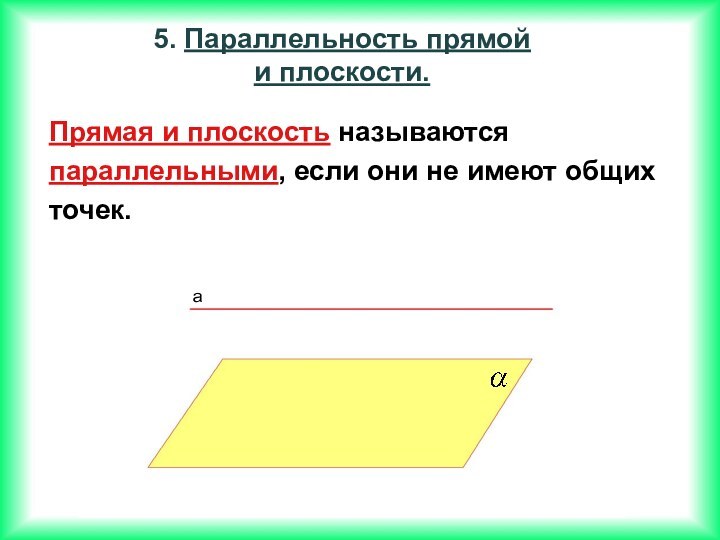
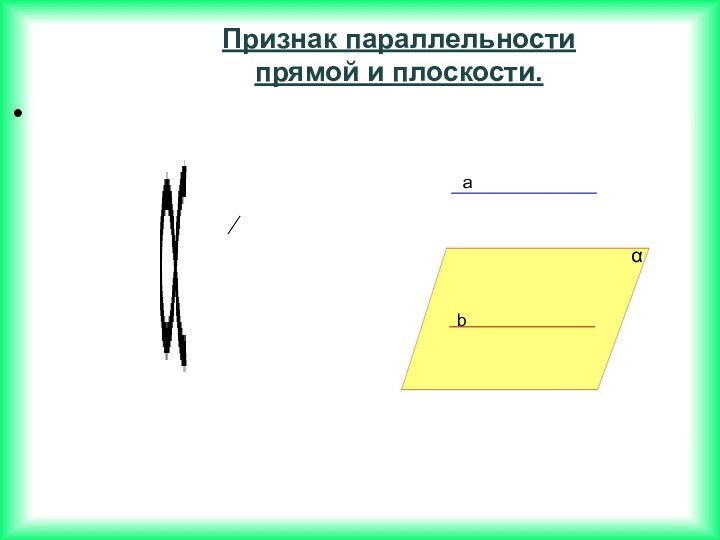
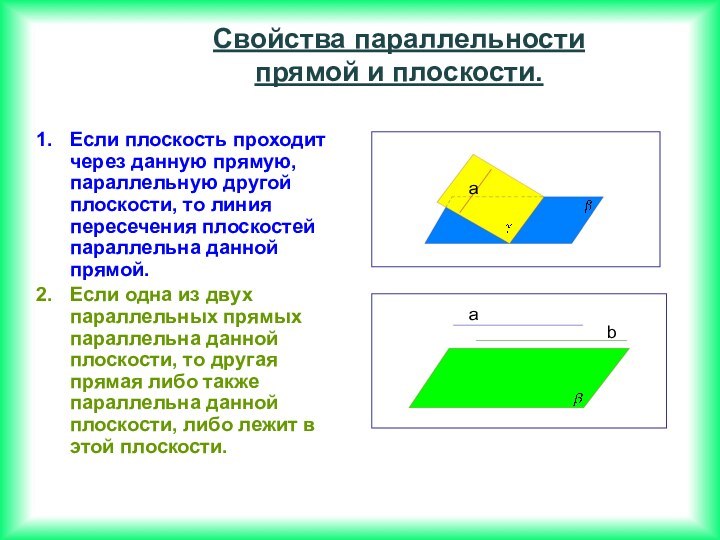
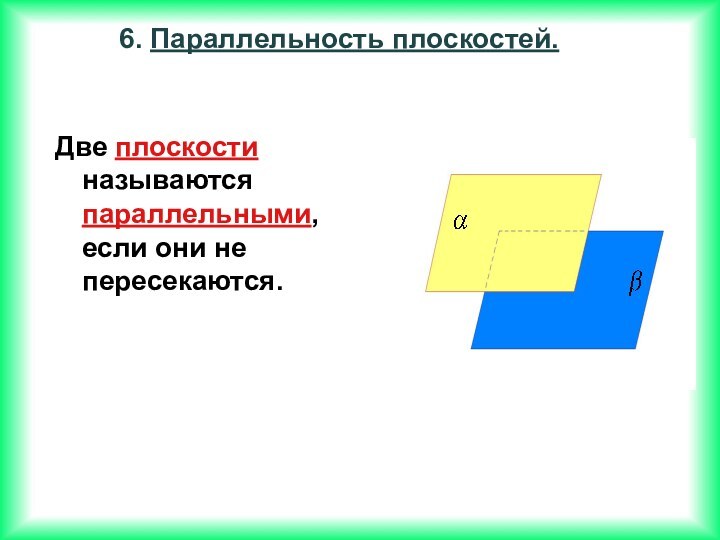
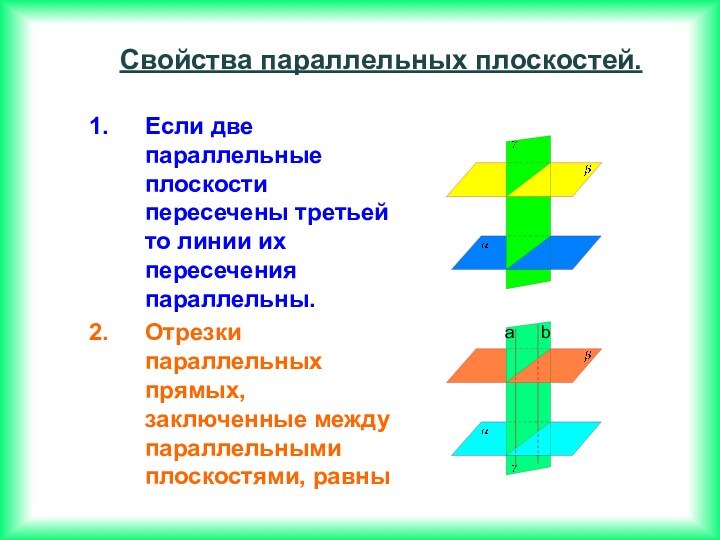
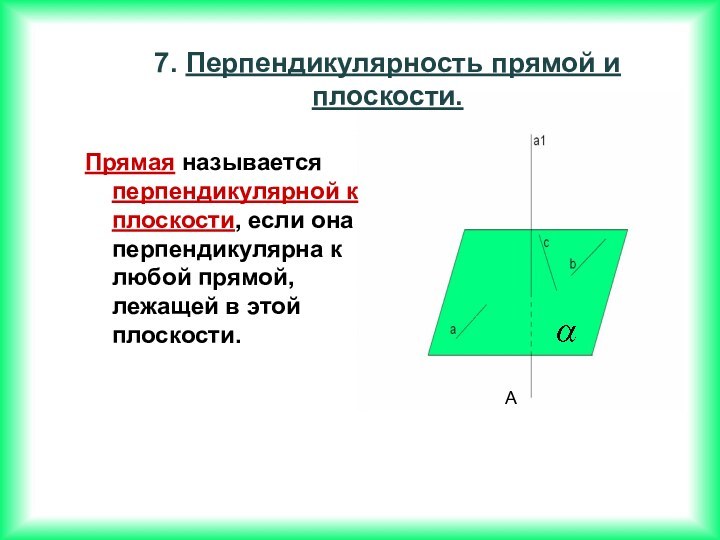
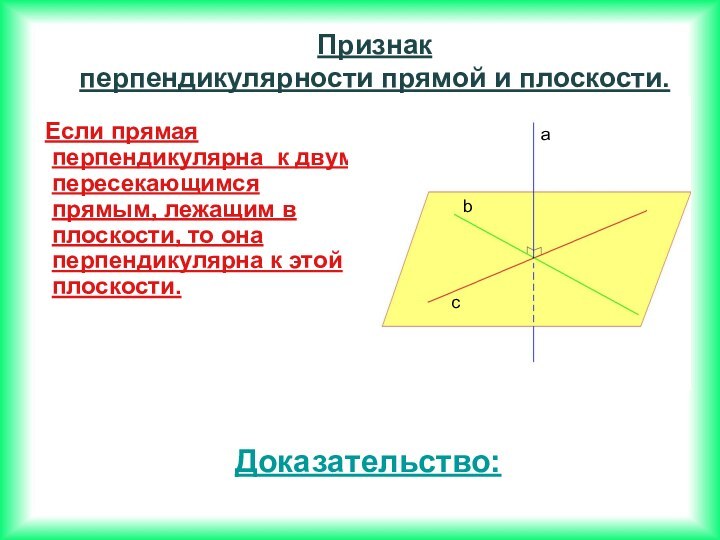
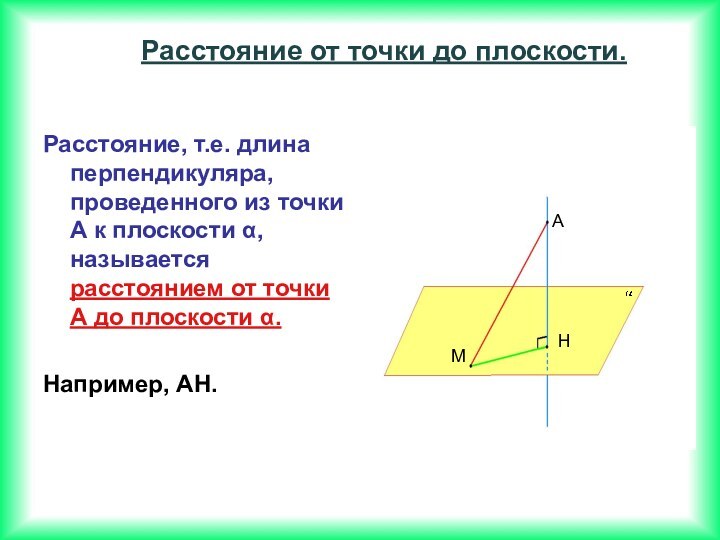
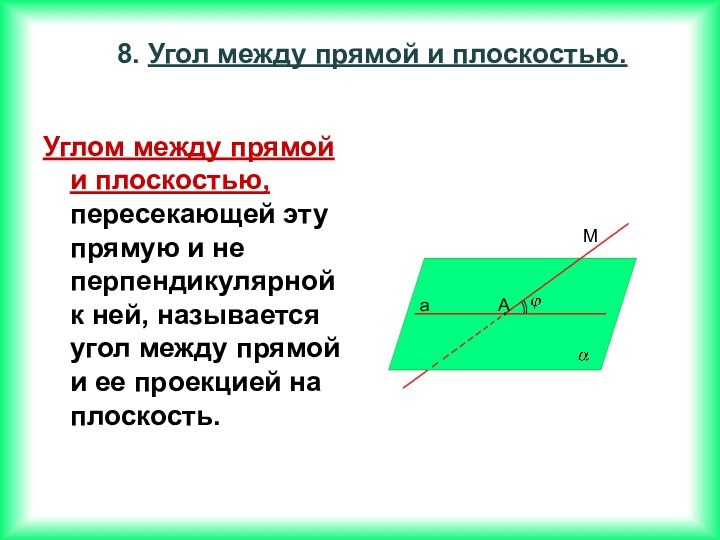
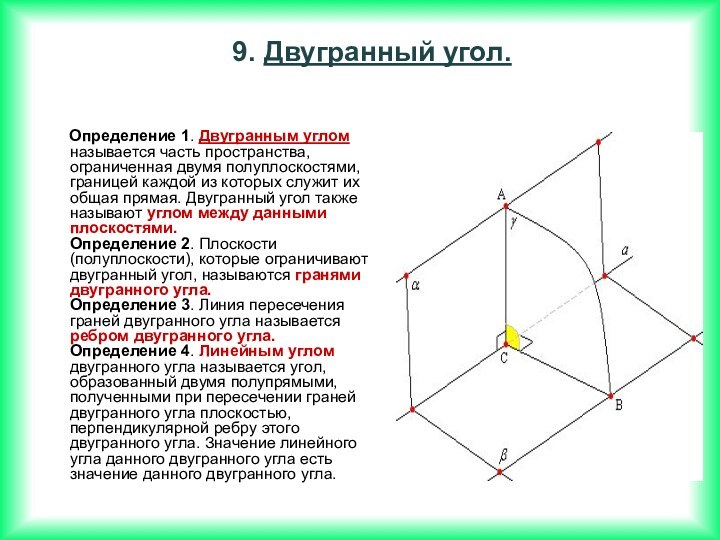
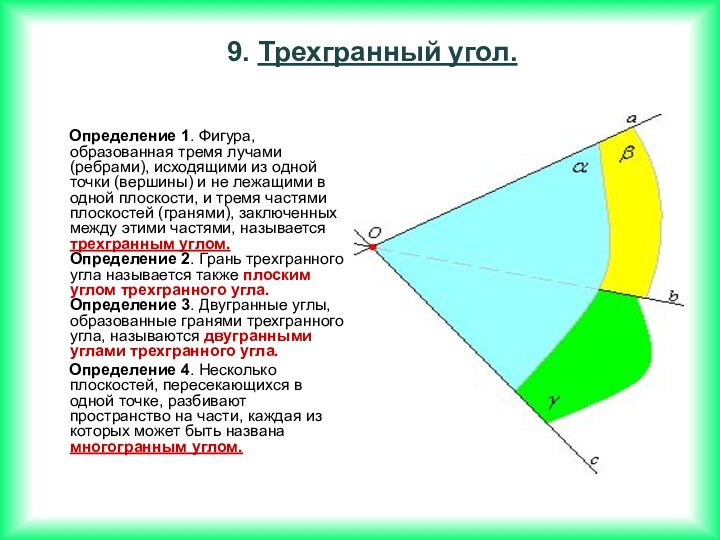
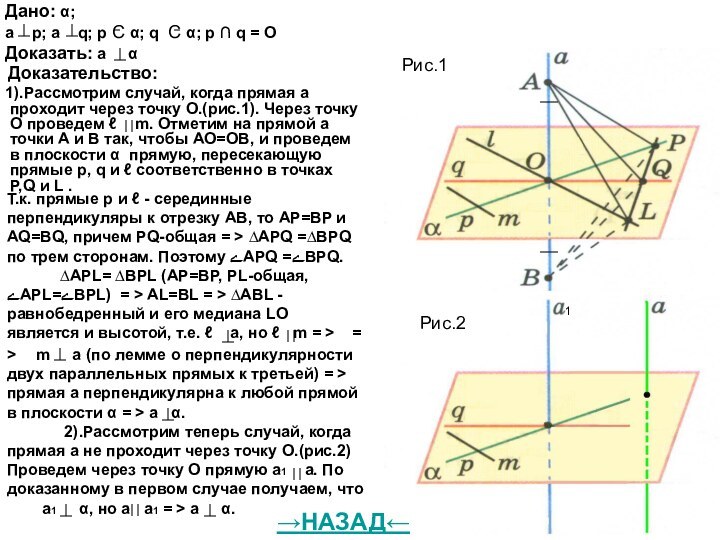
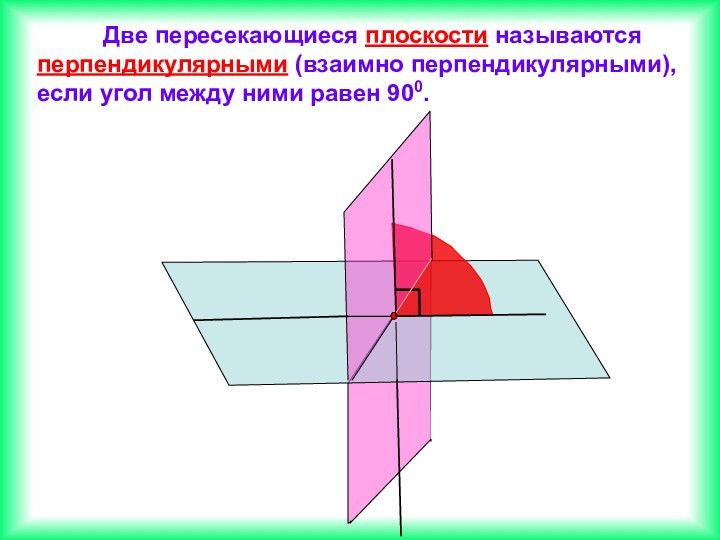
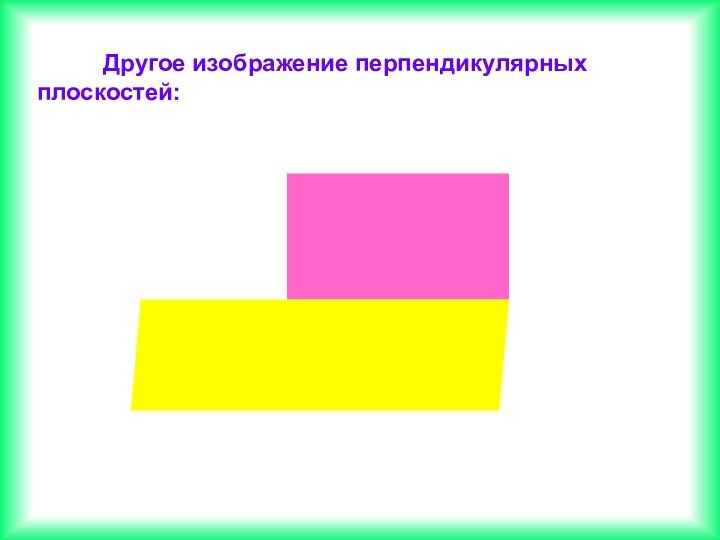
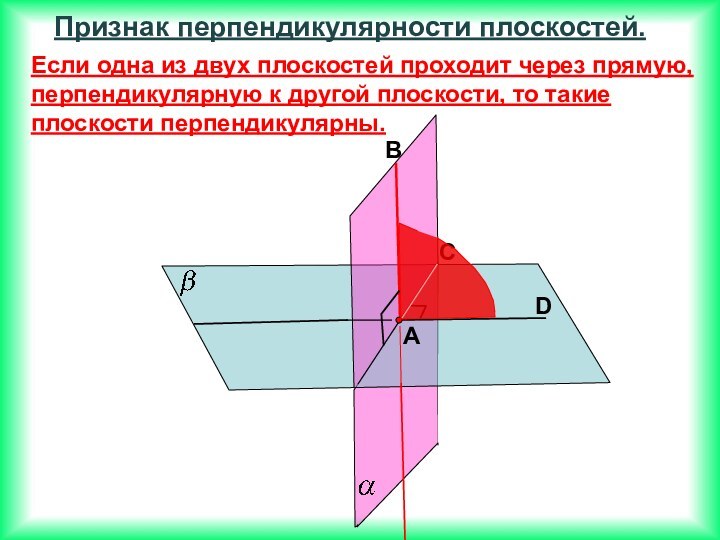
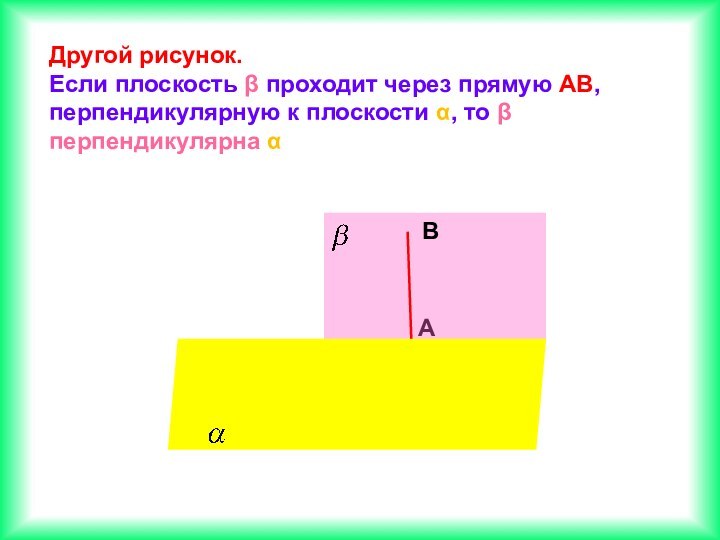
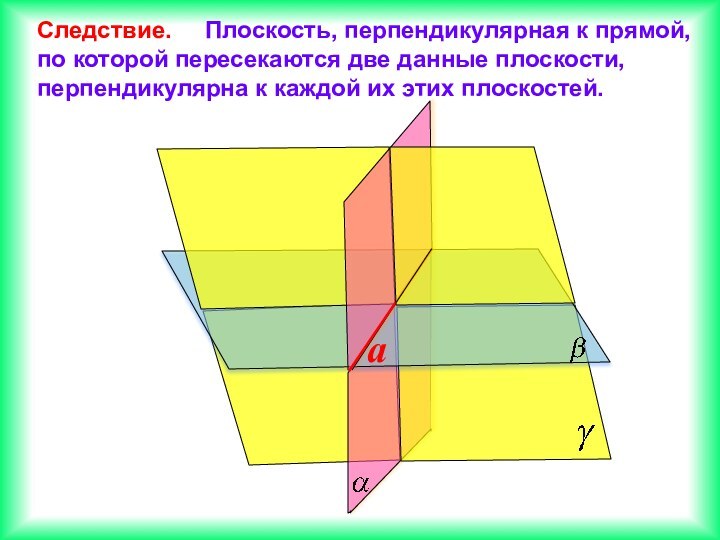
Если две прямые перпендикулярны к плоскости, то они параллельны

Дано: α
а α; b α
Доказать: а b
Доказательство:
Через какую-нибудь точку М прямой b проведем прямую b1 а. Из 1-го свойства получили прямая b1 α. Докажем, что прямая b1 совпадает с прямой b. Тем самым будет доказано, что а b. Допустим, что b1 и b не совпадают. Тогда в плоскости β, содержащей прямые b и b1, через

a

b

b1

c

M

α

β

точку М проходят две прямые, перпендикулярные к прямой с, по которой пересекаются плоскости α и β. Но это невозможно, т.к. если b α и b1 α , то эти прямые перпендикулярны любой прямой в этой плоскости(в данном случае прямой с), но согласно теореме, через точку, не лежащую на прямой можно провести только одну прямую перпендикулярную данной, следовательно, прямая а b.

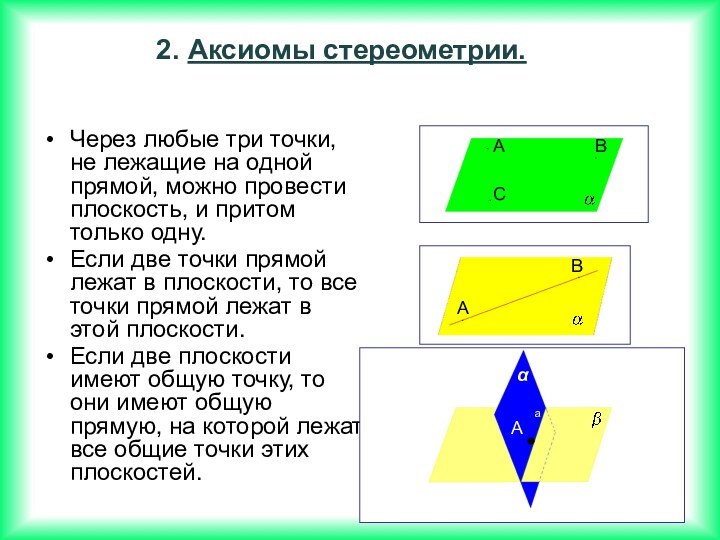
2. Если две прямые перпендикулярны плоскости, то они параллельны.

прямым, лежащим в плоскости, то она перпендикулярна к этой

плоскости.

Доказательство:

a

b

c

Признак
перпендикулярности прямой и плоскости.

перпендикуляр-ная к данной плоскости, и притом только одна.
O
A
c
Теорема о

перпендикулярности прямой и плоскости.

к плоскости α, называется расстоянием от точки А до

плоскости α.

Например, AH.

А

Н

М

Расстояние от точки до плоскости.

основание наклонной перпендикулярно к ее проекции на эту плоскость,

перпендикулярна и к самой наклонной.
Дано: α; AH- перпендикуляр к плоскости α; АМ- наклонная; а- прямая, проведенная в плоскости α через точку М перпендикулярно к проекции НМ наклонной.
Доказать: a AM
Доказательство:
Рассмотрим плоскость АМН. Прямая а перпендикулярна к этой плоскости, т.к. она перпендикулярна к двум пересекающимся прямым АН и МН, лежащим в плоскости АМН (а НМ по условию и a АН, т.к. АН α). Отсюда следует, что прямая а перпендикулярна к любой прямой, лежащей в плоскости АМН, в частности а АМ.

А

Н

М

а

α

Теорема о трех перпендикулярах.

наклонной перпендикулярно к ней, перпендикулярна к ее проекции.
А
Н
М
а
α
Обратная теорема

о трех перпендикулярах.

и не перпендикулярной к ней, называется угол между прямой

и ее проекцией на плоскость.

М

а

А

8. Угол между прямой и плоскостью.

часть пространства, ограниченная двумя полуплоскостями, границей каждой из которых

служит их общая прямая. Двугранный угол также называют углом между данными плоскостями. Определение 2. Плоскости (полуплоскости), которые ограничивают двугранный угол, называются гранями двугранного угла. Определение 3. Линия пересечения граней двугранного угла называется ребром двугранного угла. Определение 4. Линейным углом двугранного угла называется угол, образованный двумя полупрямыми, полученными при пересечении граней двугранного угла плоскостью, перпендикулярной ребру этого двугранного угла. Значение линейного угла данного двугранного угла есть значение данного двугранного угла.

9. Двугранный угол.

лучами (ребрами), исходящими из одной точки (вершины) и не

лежащими в одной плоскости, и тремя частями плоскостей (гранями), заключенных между этими частями, называется трехгранным углом. Определение 2. Грань трехгранного угла называется также плоским углом трехгранного угла. Определение 3. Двугранные углы, образованные гранями трехгранного угла, называются двугранными углами трехгранного угла.
Определение 4. Несколько плоскостей, пересекающихся в одной точке, разбивают пространство на части, каждая из которых может быть названа многогранным углом.

9. Трехгранный угол.

р; а q; р С α; q

C α; р ∩ q = О
Доказать: a α
Доказательство:
1).Рассмотрим случай, когда прямая а проходит через точку О.(рис.1). Через точку О проведем ℓ m. Отметим на прямой а точки А и B так, чтобы АО=ОВ, и проведем в плоскости α прямую, пересекающую прямые p, q и ℓ соответственно в точках P,Q и L .

Т.к. прямые p и ℓ - серединные перпендикуляры к отрезку АB, то AP=BP и AQ=BQ, причем PQ-общая = > ∆APQ =∆BPQ по трем сторонам. Поэтому ےAPQ =ےBPQ.
∆APL= ∆BPL (АР=BP, PL-общая, ےAPL=ےBPL) = > AL=BL = > ∆ABL - равнобедренный и его медиана LO является и высотой, т.е. ℓ а, но ℓ m = > = > m а (по лемме о перпендикулярности двух параллельных прямых к третьей) = > прямая а перпендикулярна к любой прямой в плоскости α = > a α.
2).Рассмотрим теперь случай, когда прямая а не проходит через точку О.(рис.2) Проведем через точку О прямую а1 а. По доказанному в первом случае получаем, что
а1 α, но а а1 = > а α.

Рис.1

Рис.2

1

→НАЗАД←

называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен

900.

плоскостей:

перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
А
С





Признак перпендикулярности

плоскостей.

β проходит через прямую АВ, перпендикулярную к плоскости α,

то β перпендикулярна α

А