Презентация на тему по математике на тему Интеграл

интеграл, проверить уровень обладания учащимися изученного
материала по данной

теме.
Развивающая: развивать мыслительную деятельность учащихся, основанную
на операциях анализа, сравнениях, обобщения, систематизации и способность
учащихся реализовать полученные знания при выполнении заданий различного
уровня;
Воспитательная: формировать мировоззренческие взгляды учащихся,
воспитывать ответственность за полученный результат, чувство успеха, взаимоответственности и самоутверждения, самоанализа, самооценки.

Знать:
Определение первообразной;
Первообразная определяется неоднозначно.
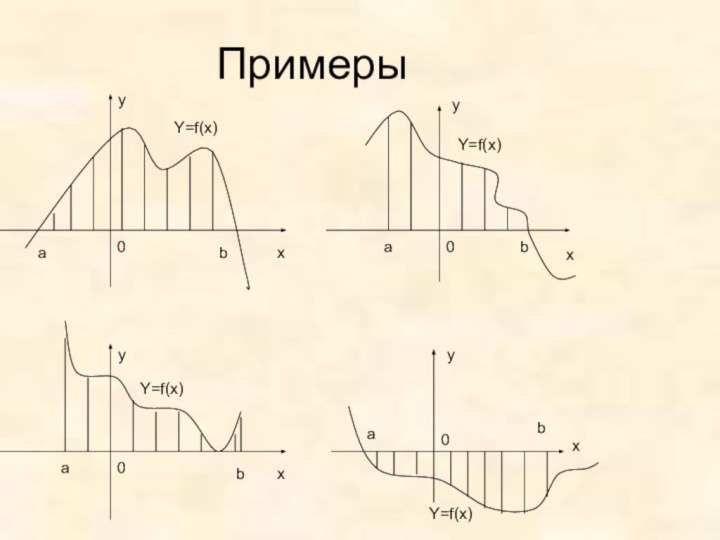
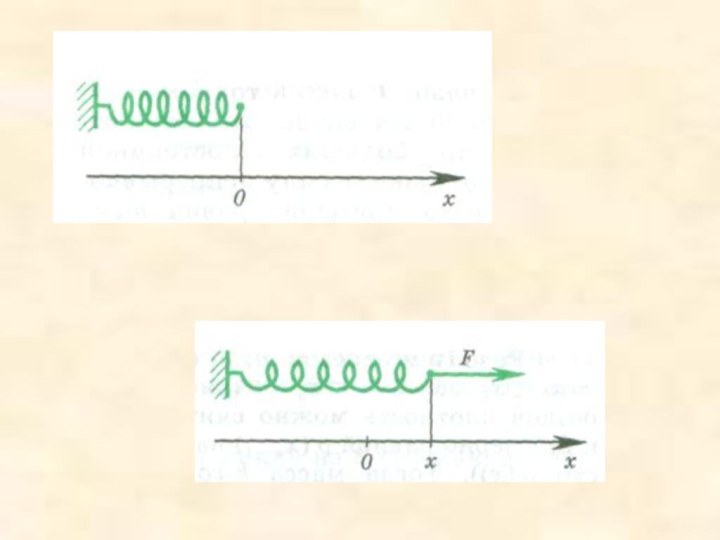
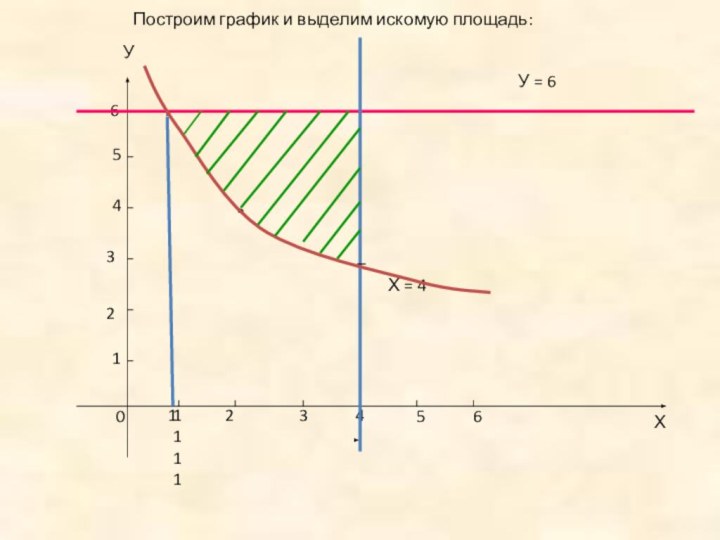
Определение криволинейной трапеции.
Алгоритм вычисления её площади.
Уметь:
Находить первообразные функций.
Находить криволинейные трапеции.
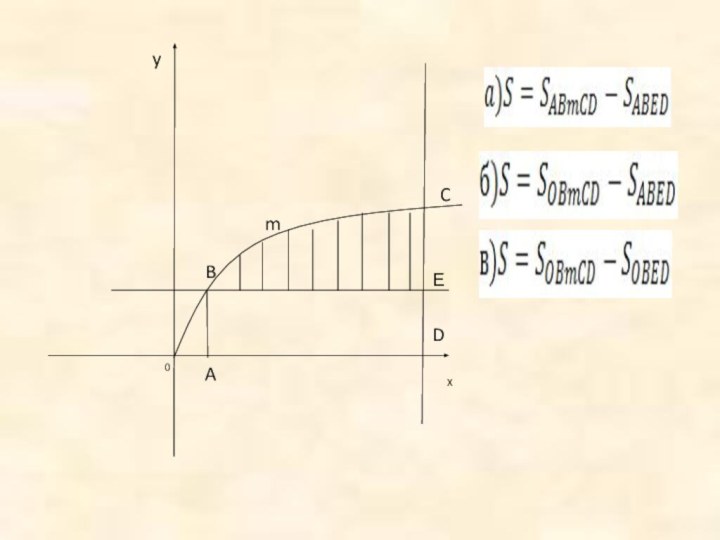
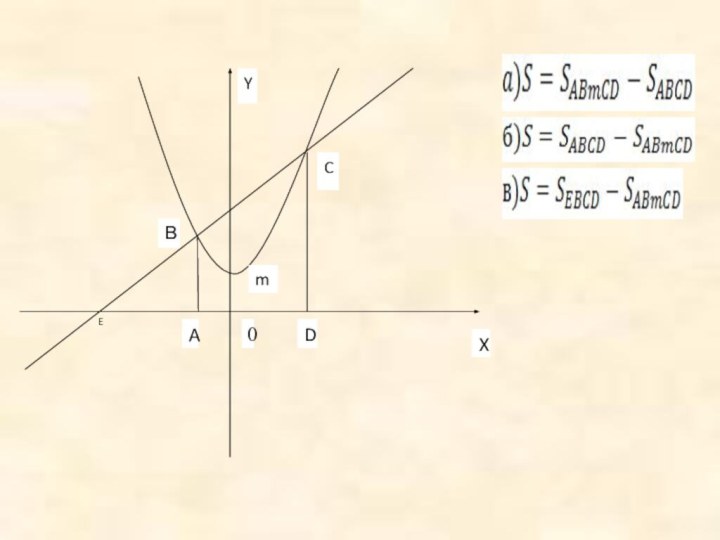
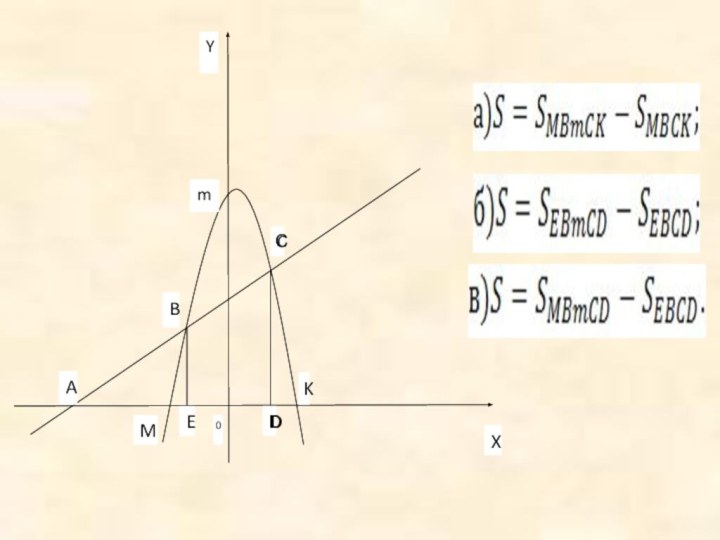
Находить площади фигур.

a
Синус угла



arcsin a = α a∈[-1;1]
Арксинус числа
(xn)' =

nxn-1
Дифференцирование

∫nxn-1dx = xn + C
Интегрирование

√x
Извлечение из корня

данном промежутке, если для любого x из этого промежутка

F’(x) = f(x).

+ 1
F3(x) = x2 + 5
F1'(x) = 2x
F2'(x) =

2x

F3'(x) = 2x

y = f(x) имеет бесконечно много первообразных вида y = F(x)+C, где
C - произвольное число

2
Если F(х)-первообразная для f(х), то kF(х)-

первообразная для kf(х)
Правило 3
Если y=F(x)- первообразная для функции y=f(x), то первообразной для функции y=f(kx+m) служит функция y=1/kF(kx+m)
Таблица первообразных

непрерывная функция f(x), не меняющей на нем знака. Фигуру,

ограниченную графиком этой функции, отрезком [а;b] и прямыми x = а и x=b, называют криволинейной трапецией.

x=а

x=b

Y=f(x)

x

y

Лейбница)
Для непрерывной функции






где F(x) – первообразная функции f(x).

линиями y=f(x) и y=g(x).
1. Строим график данных функций.

2.Найдём абсциссы точек их пересечения (границы интегрирования) из уравнения: f(x)=g(x).
Решаем его, находим x1=a,x2=b.
3.Выделяем фигуру, ограниченную данными линиями . Выясняем, является ли данная фигура криволинейной трапецией.
4.Ищем площадь данной фигуры:
Площадь криволинейной трапеции находим по формуле Ньютона-Лейбница:


где F(x) – первообразная для f(x).

x

y

a

b

A

C

B

n

Y=f(x)

Y=g(x)

от t0 до T, v(t) – скорость роста некоторой

популяции.



интеграл от скорости




по интервалу времени ее размножения.

форме клумба не должна быть круглой, квадратной или прямоугольной.

Она должна содержать в себе прямые и кривые линии. Пусть она будет плоской фигурой, ограниченной линиями Y=4/X+2; X=4; Y=6. Необходима еще подсчитать сколько денег можно получить за вскапывания этой клумбы, если за каждый м² выплачивают 50 руб…?

искомую площадь:

условию,
y=4/x+4 и y=6,
следовательно

4/x+2=6;
4/x=4
х = 1

4

4 4
S=∫(6-4/x-2)dx=∫ (4-4/x)dx=(4x-4ln|x|)|=
1 1 1
16-4ln4-4+4ln1=12-4ln4 ≈ 6,4(м²)