Презентация на тему График степенной функции

Содержание

2. Эпиграфом нашего урока являются слова А. Эйнштейна:
3. Цели урока Повторить свойства и график
4. Функция График функции- кубическая парабола.1) Д(f)=R;2) E(f)=R;3)
5. Число a- отвечает за перемещение вдоль оси
6. Функция График функции- гипербола.1) Д(y)=R, кроме х=02)
7. Число а- отвечает за перемещение вдоль оси
8. Функция 1) Д(y)=
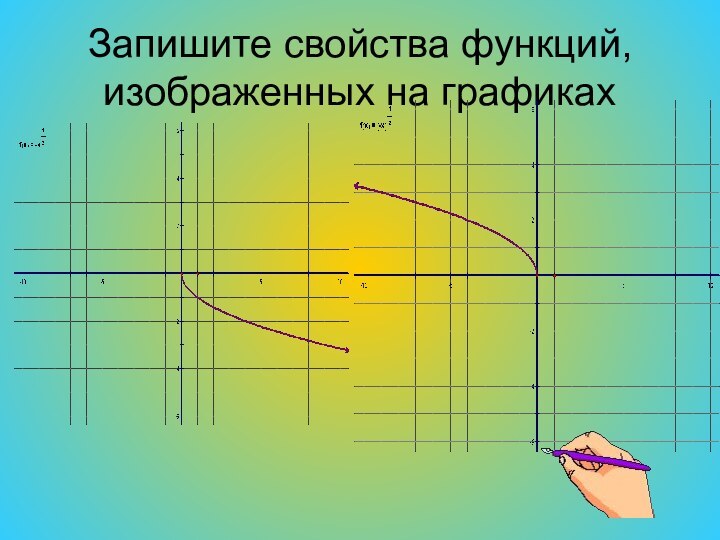
9. Запишите свойства функций, изображенных на графиках
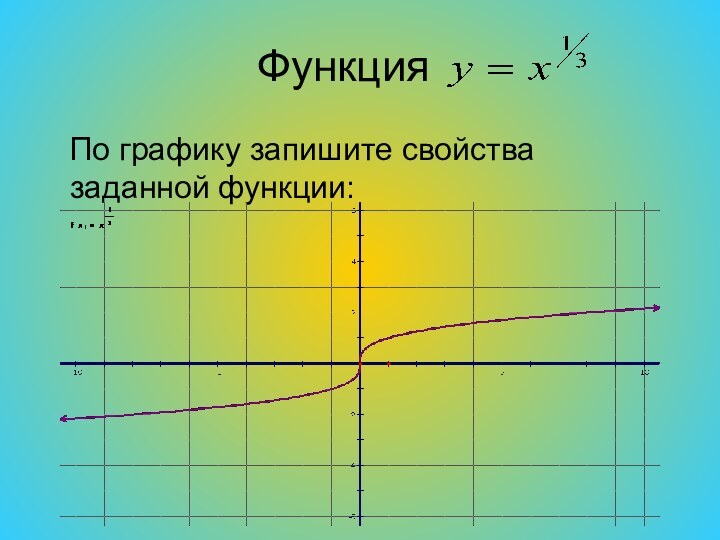
11. Функция По графику запишите свойства заданной функции:
12. Постройте графики заданных функций
13. Итог урока: Построение графика какой функции
14. Скачать презентацию
15. Похожие презентации

Эпиграфом нашего урока являются слова А. Эйнштейна: “Весь наш предшествующий опыт приводит к убеждению, что природа является осуществлением того, что математически проще всего представить”.

Главная
Алгебра
График степенной функции

Степенная функцияУрок обобщения Презентация подготовила и выполнила Шурыгина И.В.

Эпиграфом нашего урока являются слова А. Эйнштейна: “Весь наш предшествующий опыт

Цели урока Повторить свойства и график степенной функции; закрепить навыки

Функция График функции- кубическая парабола.1) Д(f)=R;2) E(f)=R;3) Нули функции: x=04) Знакопостоянство

Число a- отвечает за перемещение вдоль оси ОХ;если а 0, то влево

Функция График функции- гипербола.1) Д(y)=R, кроме х=02) E(y)=R, кроме y=03) Нули функции:

Число а- отвечает за перемещение вдоль оси OX;если ,

Запишите свойства функций, изображенных на графиках

Функция По графику запишите свойства заданной функции:

Итог урока: Построение графика какой функции мы сегодня с вами повторили?

Домашнее задание: Составить и построить графики степенной функции на каждый вид

Слайды презентации

Слайд 2 Эпиграфом нашего урока являются слова А. Эйнштейна:
“Весь

наш предшествующий опыт приводит к убеждению, что природа является осуществлением

того, что математически проще всего представить”.

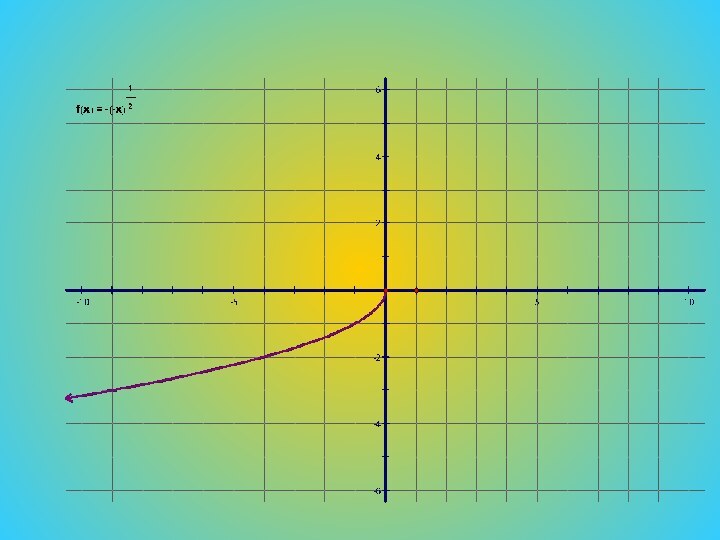
Слайд 3 Цели урока
Повторить свойства и график степенной

Цели урока Повторить свойства и график степенной функции; закрепить навыки построения

функции;
закрепить навыки построения графиков и их описания

с использованием программы «Живая геометрия»;
продолжить работу над умением анализировать поставленную задачу, предполагаемый результат и обобщать;
Воспитывать чувство взаимовыручки, коллективизма.

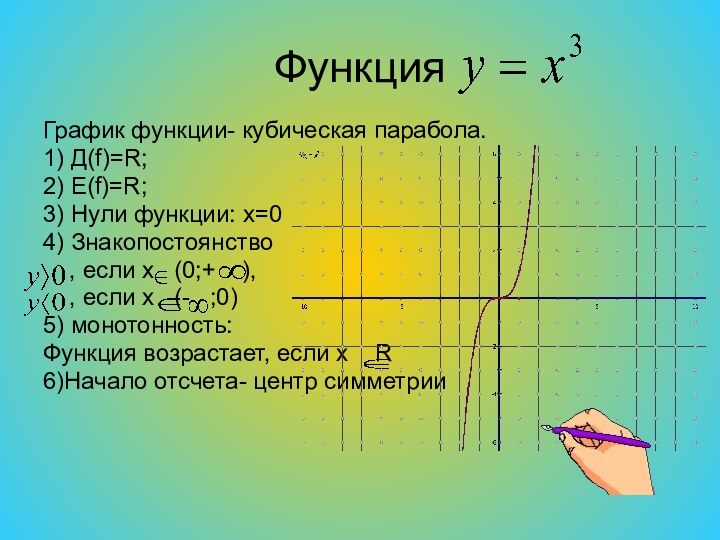
Слайд 4 Функция
График функции- кубическая парабола.
1) Д(f)=R;
2) E(f)=R;
3) Нули

функции: x=0
4) Знакопостоянство
, если x (0;+

),
, если x (- ;0)
5) монотонность:
Функция возрастает, если x R
6)Начало отсчета- центр симметрии

Слайд 5
Число a- отвечает за перемещение вдоль оси ОХ;
если

Число a- отвечает за перемещение вдоль оси ОХ;если а 0, то

а 0,
то влево на а единиц от 0;
если

а 0,
то вправо на а единиц от 0.

Число b-отвечает за перемещение вдоль оси OY;
если b 0,
то вверх на b единиц от 0 ;
если b 0,
то вниз на b единиц от 0.

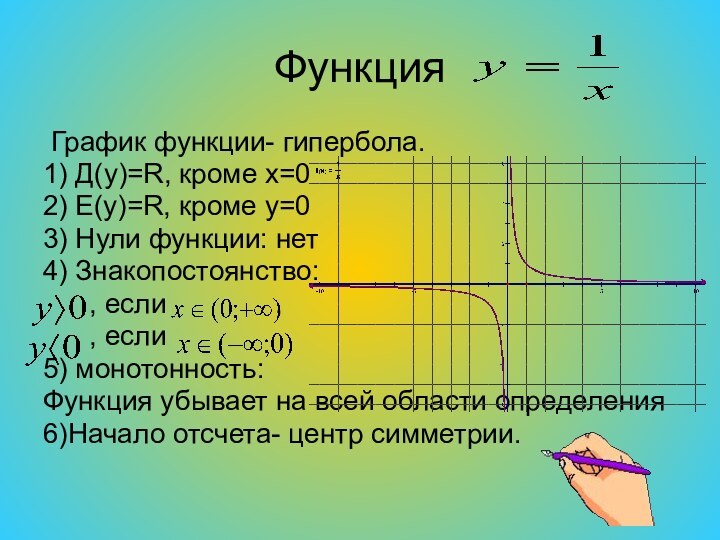
Слайд 6 Функция
График функции- гипербола.
1) Д(y)=R, кроме х=0
2)

Функция График функции- гипербола.1) Д(y)=R, кроме х=02) E(y)=R, кроме y=03) Нули

E(y)=R, кроме y=0
3) Нули функции: нет
4) Знакопостоянство:

, если ,
, если
5) монотонность:
Функция убывает на всей области определения
6)Начало отсчета- центр симметрии.

Слайд 7
Число а- отвечает за перемещение вдоль оси OX;
если

Число а- отвечает за перемещение вдоль оси OX;если , то

,
то влево на a единиц

от 0;
если ,
то вправо на а единиц от 0.

Число b- отвечает за перемещение вдоль оси OY;
если ,
то вверх на b единиц от 0;
если ,
то вниз на b единиц от 0.