- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике Построение циркулем и линейкой
Содержание
- 2. Цели урока:дать представление о задачах на построение;рассмотреть наиболее простые задачи на построение и научить решать их.
- 3. Задачи на построение – это такие задачи,
- 4. Что можно сделать с помощью циркуля и
- 5. Схема решения задач на построение:Анализ (рисунок искомой
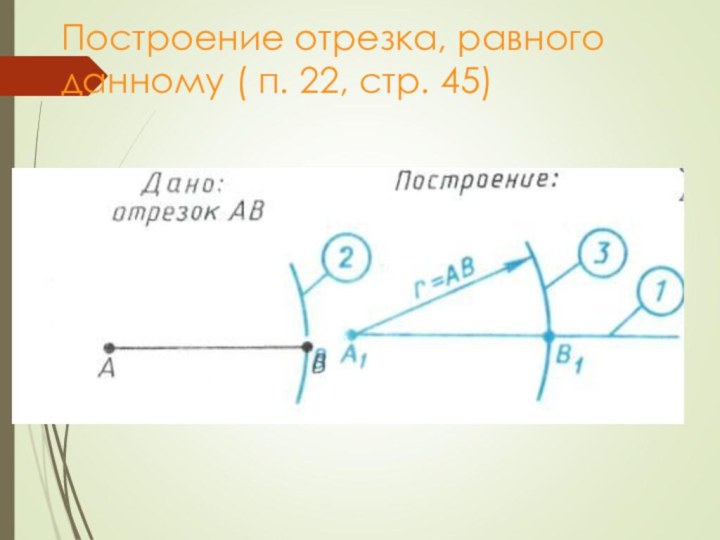
- 6. Построение отрезка, равного данному ( п. 22, стр. 45)
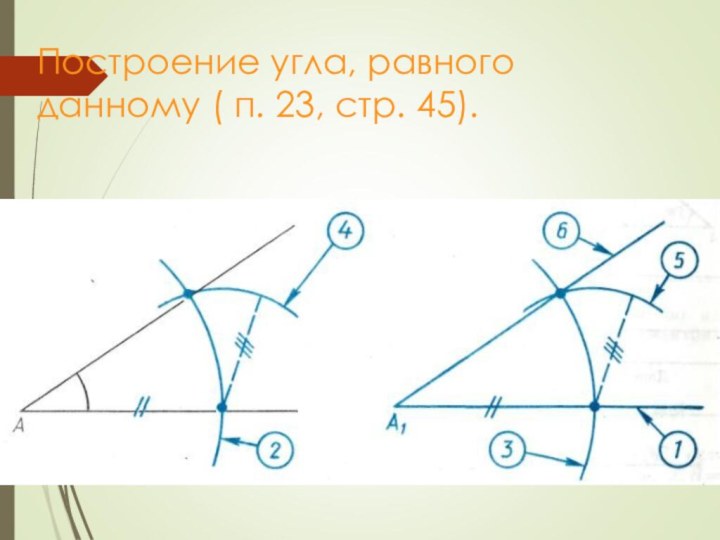
- 7. Построение угла, равного данному ( п. 23, стр. 45).
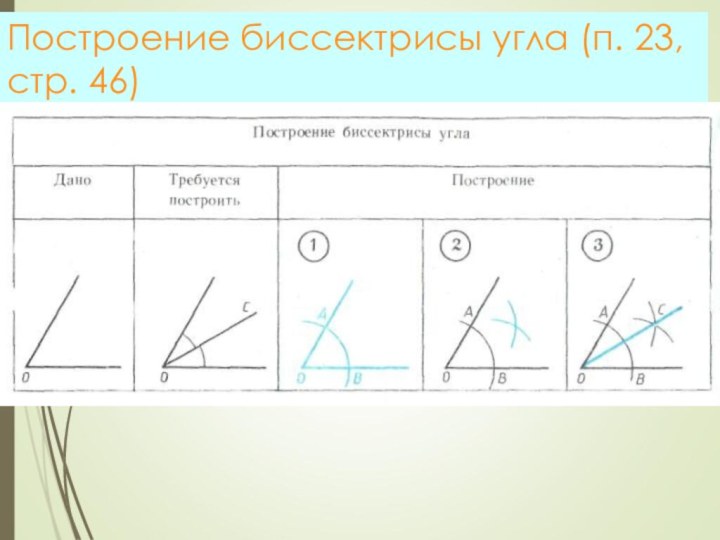
- 8. Построение биссектрисы угла (п. 23, стр. 46)
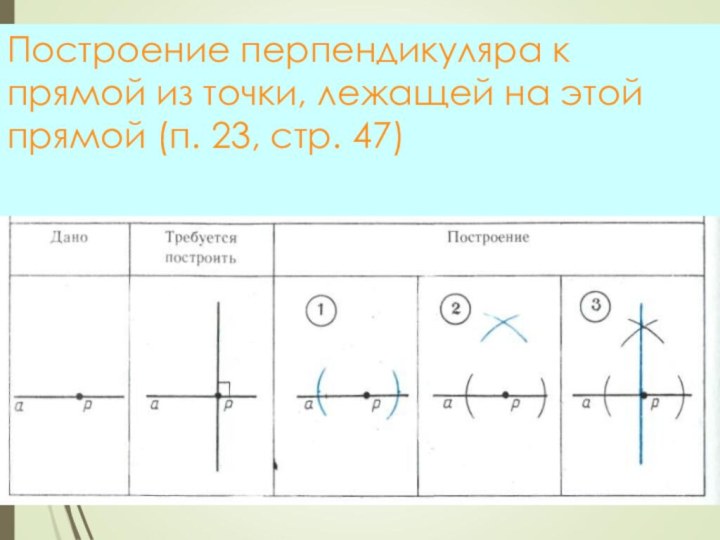
- 9. Построение перпендикуляра к прямой из точки, лежащей на этой прямой (п. 23, стр. 47)
- 10. Построение серединного перпендикуляра отрезка и нахождение середины отрезка (п. 23, стр. 48)
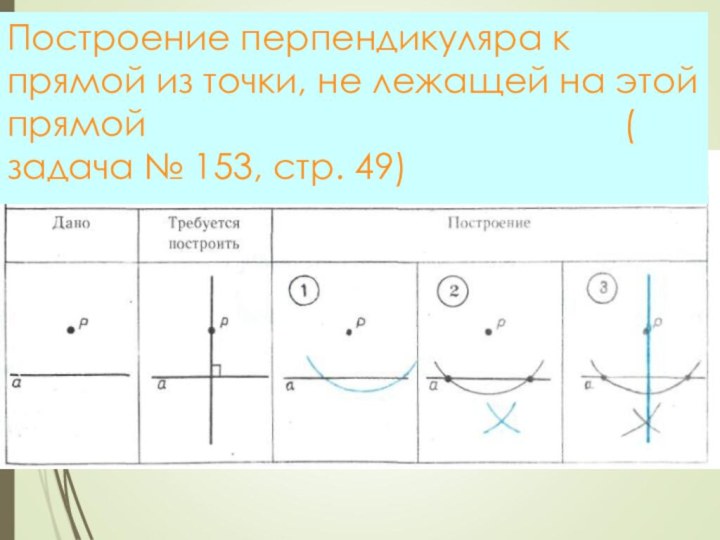
- 11. Построение перпендикуляра к прямой из точки, не
- 12. Скачать презентацию
- 13. Похожие презентации
Цели урока:дать представление о задачах на построение;рассмотреть наиболее простые задачи на построение и научить решать их.







Слайд 2
Цели урока:
дать представление о задачах на построение;
рассмотреть наиболее
простые задачи на построение и научить решать их.
Слайд 3 Задачи на построение – это такие задачи, при
решении которых нужно построить геометрическую фигуру, удовлетворяющую условиям задачи,
с помощью циркуля и линейки без делений.
Слайд 4
Что можно сделать с помощью циркуля и линейки?
Линейка
позволяет провести:
-произвольную прямую; - прямую, проходящую через две данные точки.С помощью циркуля можно провести: - окружность произвольного радиуса; - окружность с центром в данной точке и радиусом, равным данному отрезку.
Слайд 5
Схема решения задач на построение:
Анализ (рисунок искомой фигуры,
устанавливающий связи между данными задачи и искомыми элементами, и
план построения).Построение по намеченному плану.
Доказательство, что данная фигура удовлетворяет условиям задачи.
Исследование (при любых ли данных задача имеет решение, и если имеет, то сколько).