- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Risk and Return
Содержание
- 2. Topics CoveredMarkowitz Portfolio TheoryRisk and Return RelationshipTesting the CAPMCAPM Alternatives
- 3. Markowitz Portfolio TheoryCombining stocks into portfolios can
- 4. Markowitz Portfolio TheoryPrice changes vs. Normal distributionMicrosoft
- 5. Markowitz Portfolio TheoryStandard Deviation VS. Expected ReturnInvestment A % probability% return
- 6. Markowitz Portfolio TheoryStandard Deviation VS. Expected ReturnInvestment B % probability% return
- 7. Markowitz Portfolio TheoryStandard Deviation VS. Expected ReturnInvestment C % probability% return
- 8. Markowitz Portfolio TheoryStandard Deviation VS. Expected ReturnInvestment D % probability% return
- 9. Markowitz Portfolio TheoryCoca ColaReebokStandard DeviationExpected Return (%)35%
- 10. Efficient FrontierStandard DeviationExpected Return (%)Each half egg
- 11. Efficient FrontierStandard DeviationExpected Return (%)Lending or Borrowing
- 12. Efficient FrontierExample
- 13. Efficient FrontierExample
- 14. Efficient FrontierExample
- 15. Efficient FrontierExample
- 16. Efficient FrontierABReturnRisk (measured as σ)
- 17. Efficient FrontierABReturnRiskAB
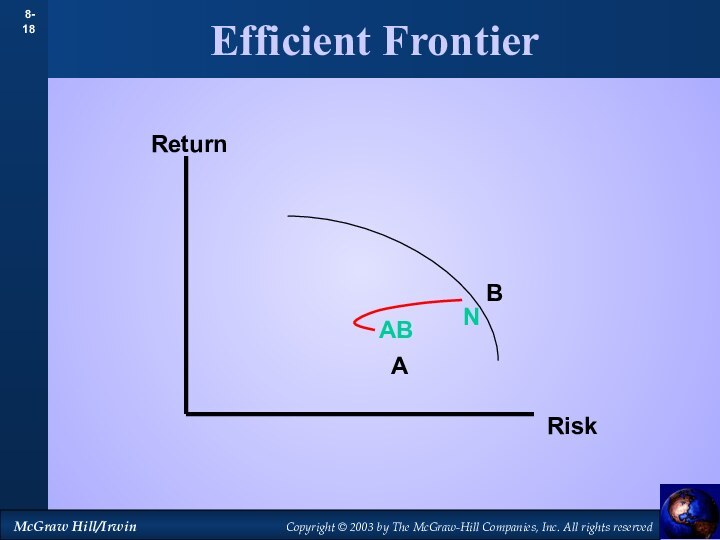
- 18. Efficient FrontierABNReturnRiskAB
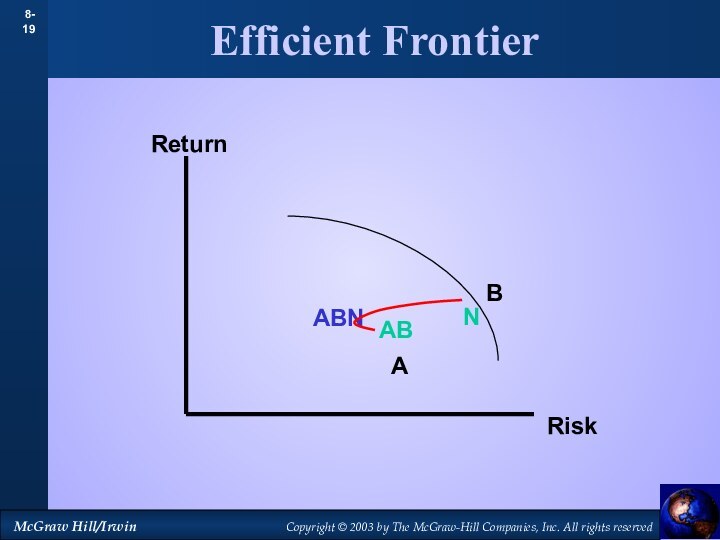
- 19. Efficient FrontierABNReturnRiskABABN
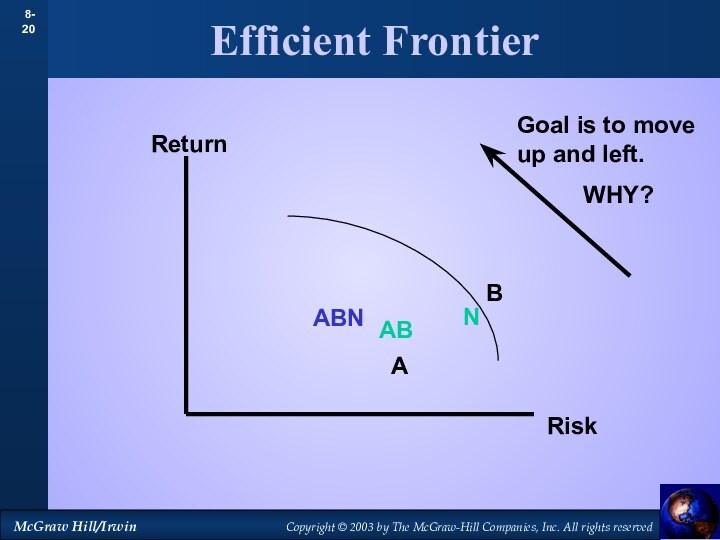
- 20. Efficient FrontierABNReturnRiskABGoal is to move up and left. WHY?ABN
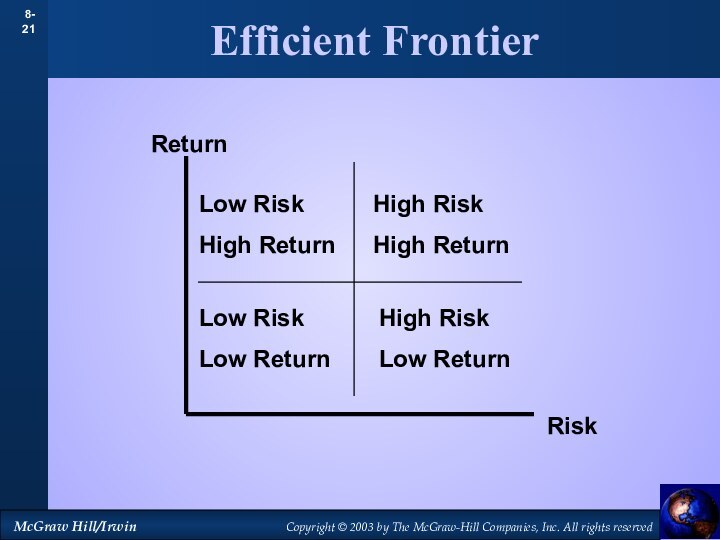
- 21. Efficient FrontierReturnRiskLow RiskHigh ReturnHigh RiskHigh ReturnLow RiskLow ReturnHigh RiskLow Return
- 22. Efficient FrontierReturnRiskLow RiskHigh ReturnHigh RiskHigh ReturnLow RiskLow ReturnHigh RiskLow Return
- 23. Efficient FrontierReturnRiskABNABABN
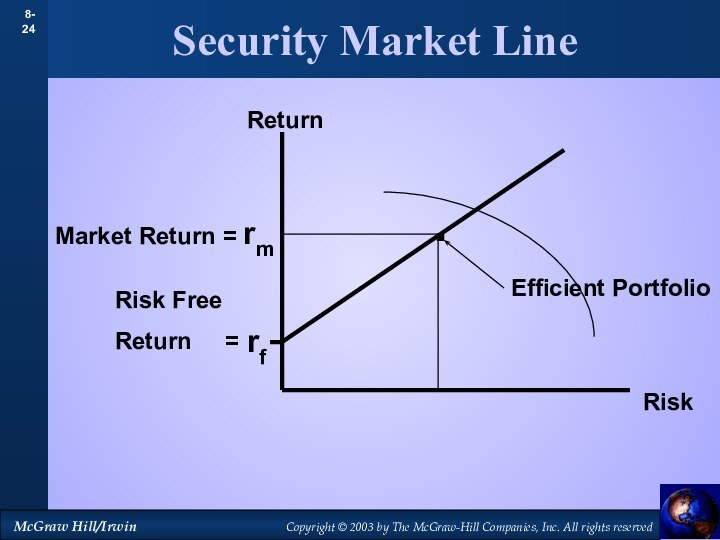
- 24. Security Market LineReturnRisk.rfRisk Free Return =Efficient Portfolio
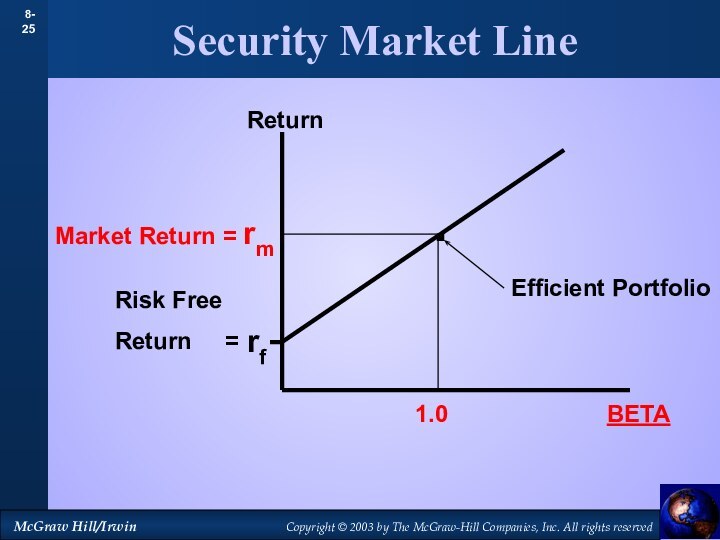
- 25. Security Market LineReturn.rfRisk Free Return =Efficient PortfolioBETA1.0
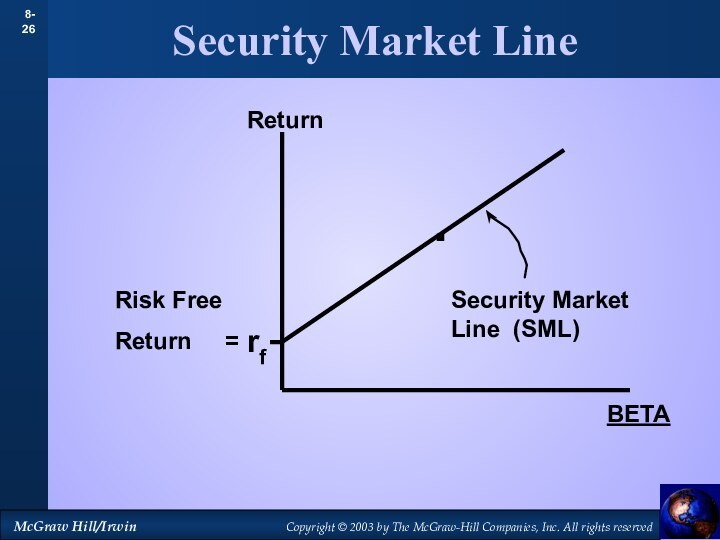
- 26. Security Market LineReturn.rfRisk Free Return =BETASecurity Market Line (SML)
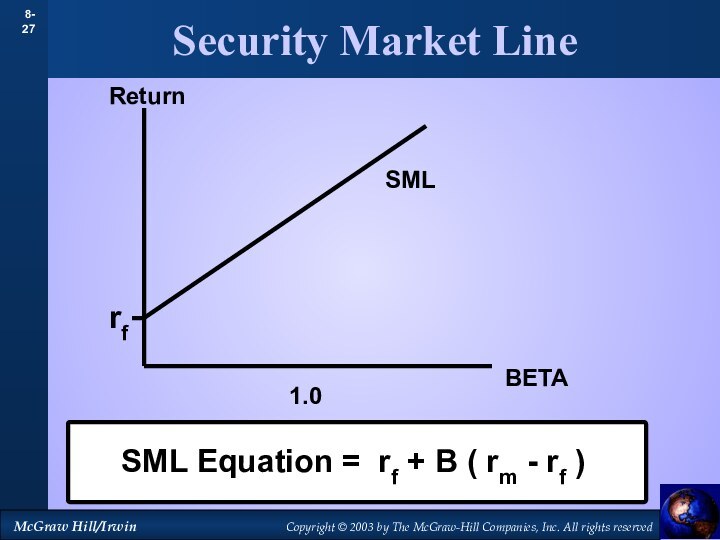
- 27. Security Market LineReturnBETArf1.0SMLSML Equation = rf + B ( rm - rf )
- 28. Capital Asset Pricing Model R = rf + B ( rm - rf )CAPM
- 29. Testing the CAPMAvg Risk Premium 1931-65Portfolio Beta1.0SML3020100InvestorsMarket PortfolioBeta vs. Average Risk Premium
- 30. Testing the CAPMAvg Risk Premium 1966-91Portfolio Beta1.0SML3020100InvestorsMarket PortfolioBeta vs. Average Risk Premium
- 31. Testing the CAPMHigh-minus low book-to-marketReturn vs. Book-to-MarketDollarsLow minus bighttp://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html
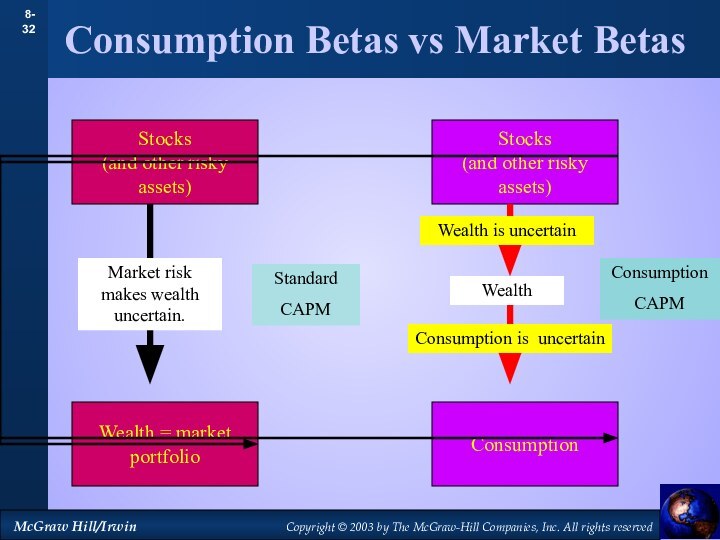
- 32. Consumption Betas vs Market BetasStocks (and other risky assets)Wealth = marketportfolio
- 33. Arbitrage Pricing Theory Alternative to CAPMExpected Risk
- 34. Скачать презентацию
- 35. Похожие презентации
Topics CoveredMarkowitz Portfolio TheoryRisk and Return RelationshipTesting the CAPMCAPM Alternatives









Слайд 3
Markowitz Portfolio Theory
Combining stocks into portfolios can reduce
standard deviation, below the level obtained from a simple
weighted average calculation.Correlation coefficients make this possible.
The various weighted combinations of stocks that create this standard deviations constitute the set of efficient portfolios.
Слайд 4
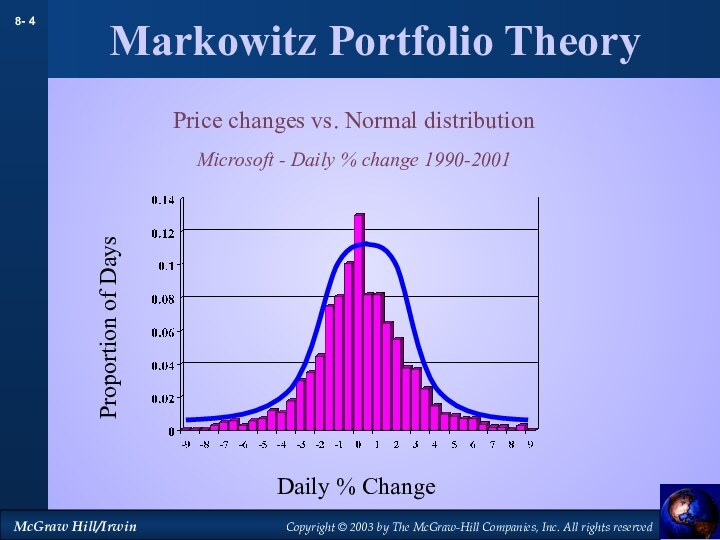
Markowitz Portfolio Theory
Price changes vs. Normal distribution
Microsoft -
Daily % change 1990-2001
Proportion of Days
Daily %
Change
Слайд 5
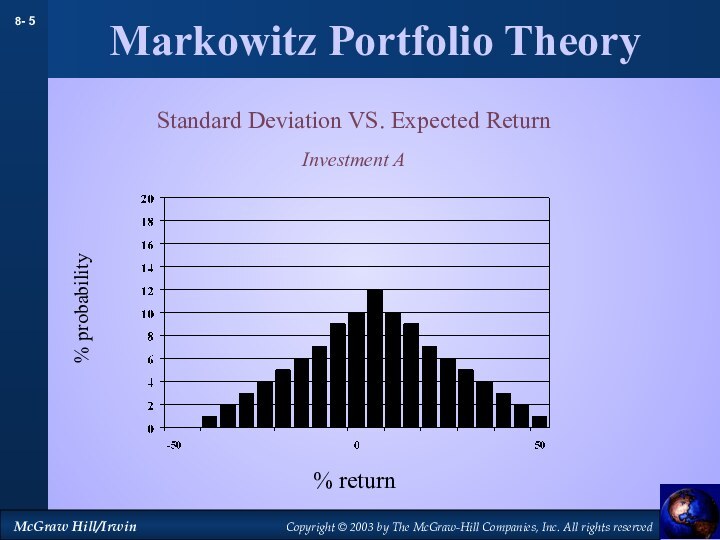
Markowitz Portfolio Theory
Standard Deviation VS. Expected Return
Investment A
% probability
% return
Слайд 6
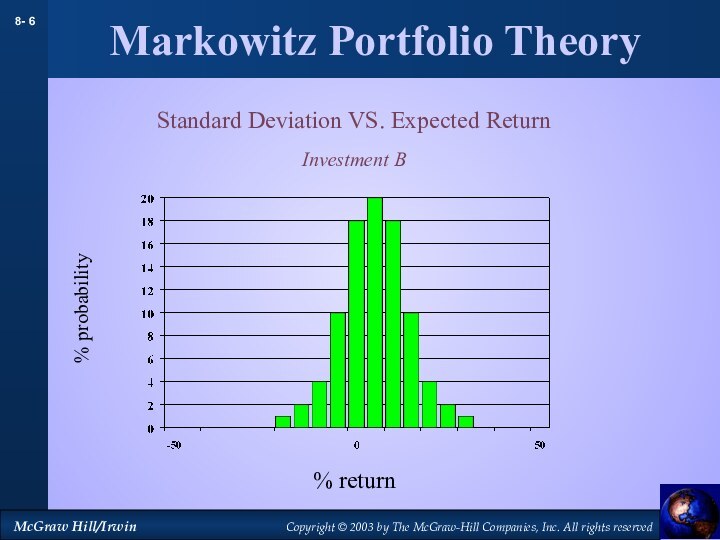
Markowitz Portfolio Theory
Standard Deviation VS. Expected Return
Investment B
% probability
% return
Слайд 7
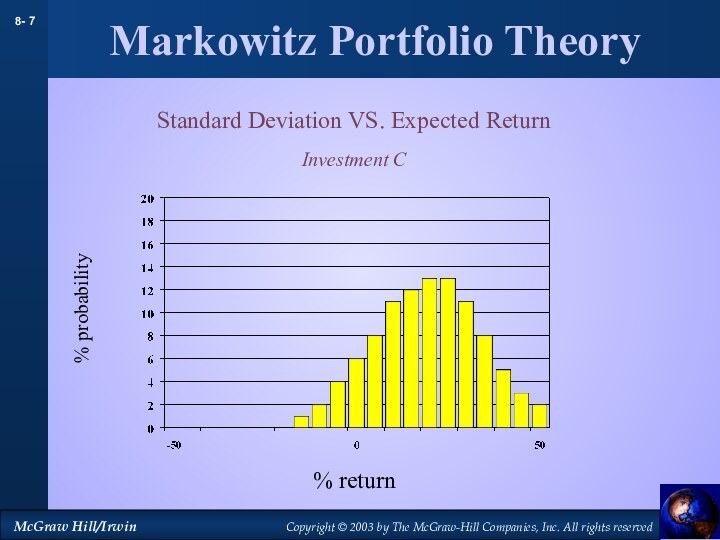
Markowitz Portfolio Theory
Standard Deviation VS. Expected Return
Investment C
% probability
% return
Слайд 8
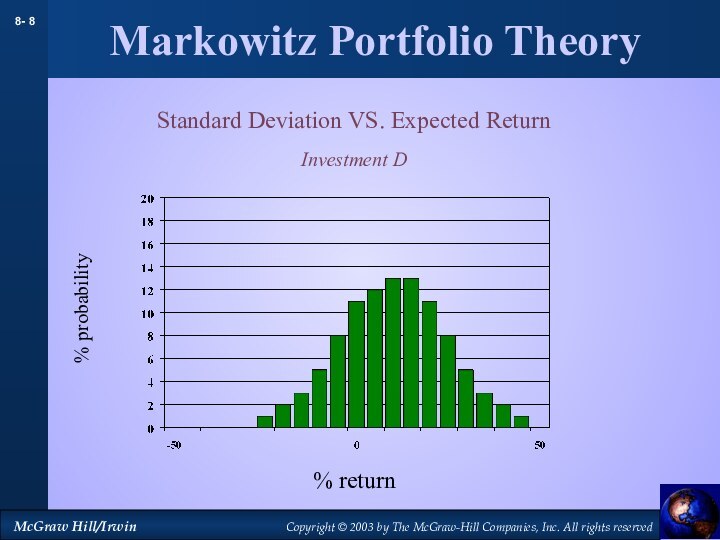
Markowitz Portfolio Theory
Standard Deviation VS. Expected Return
Investment D
% probability
% return
Слайд 9
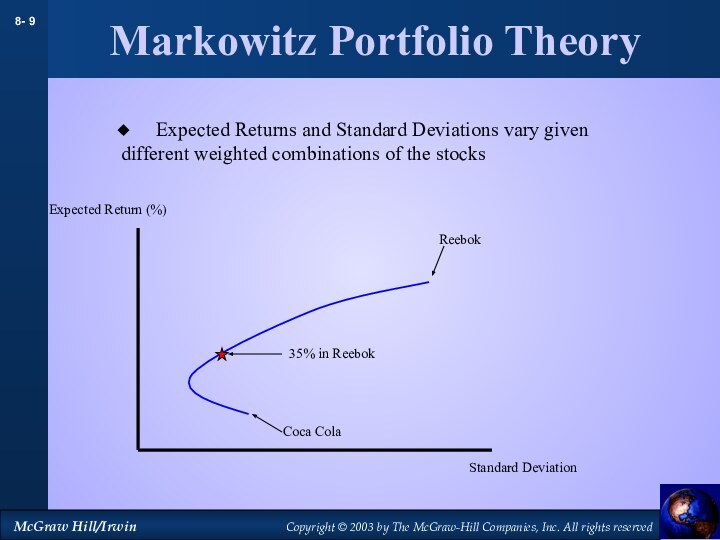
Markowitz Portfolio Theory
Coca Cola
Reebok
Standard Deviation
Expected Return (%)
35% in
Reebok
Expected Returns and Standard Deviations vary
given different weighted combinations of the stocks
Слайд 10
Efficient Frontier
Standard Deviation
Expected Return (%)
Each half egg shell
represents the possible weighted combinations for two stocks.
The composite
of all stock sets constitutes the efficient frontier
Слайд 11
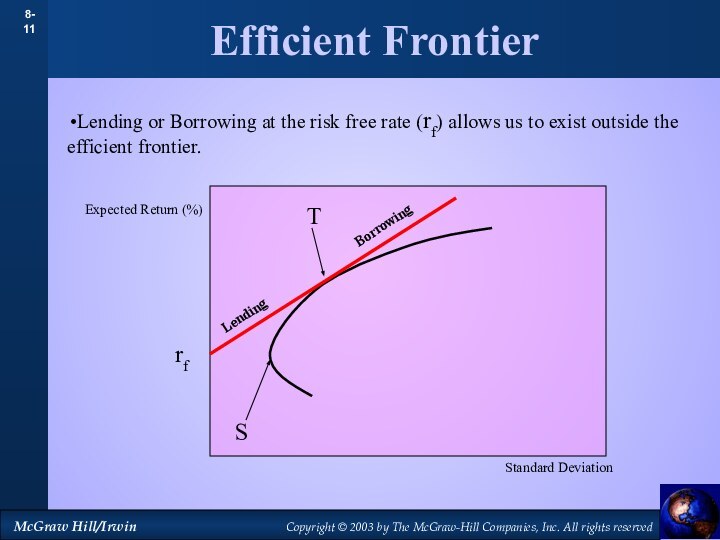
Efficient Frontier
Standard Deviation
Expected Return (%)
Lending or Borrowing at
the risk free rate (rf) allows us to exist
outside the efficient frontier.rf
Lending Borrowing
T
S
Слайд 12
Efficient Frontier
Example
Correlation Coefficient =
.4Stocks σ % of Portfolio Avg Return
ABC Corp 28 60% 15%
Big Corp 42 40% 21%
Standard Deviation = weighted avg = 33.6
Standard Deviation = Portfolio = 28.1
Return = weighted avg = Portfolio = 17.4%
Слайд 13
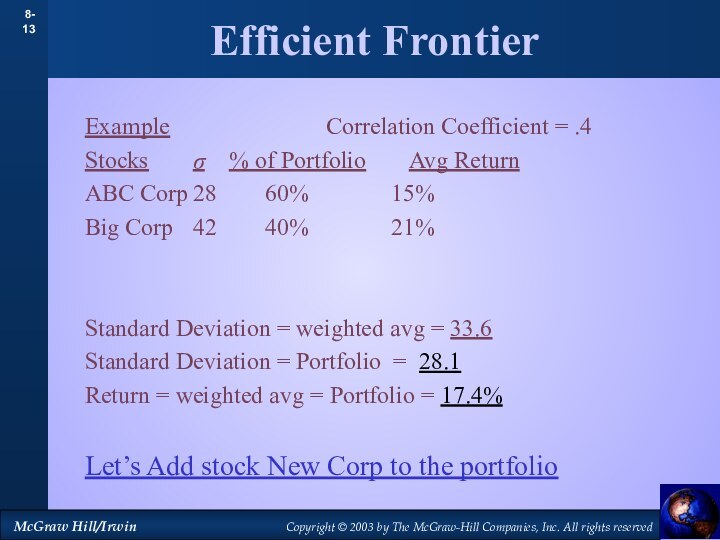
Efficient Frontier
Example
Correlation Coefficient =
.4Stocks σ % of Portfolio Avg Return
ABC Corp 28 60% 15%
Big Corp 42 40% 21%
Standard Deviation = weighted avg = 33.6
Standard Deviation = Portfolio = 28.1
Return = weighted avg = Portfolio = 17.4%
Let’s Add stock New Corp to the portfolio
Слайд 14
Efficient Frontier
Example
Correlation Coefficient =
.3Stocks σ % of Portfolio Avg Return
Portfolio 28.1 50% 17.4%
New Corp 30 50% 19%
NEW Standard Deviation = weighted avg = 31.80
NEW Standard Deviation = Portfolio = 23.43
NEW Return = weighted avg = Portfolio = 18.20%
Слайд 15
Efficient Frontier
Example
Correlation Coefficient =
.3Stocks σ % of Portfolio Avg Return
Portfolio 28.1 50% 17.4%
New Corp 30 50% 19%
NEW Standard Deviation = weighted avg = 31.80
NEW Standard Deviation = Portfolio = 23.43
NEW Return = weighted avg = Portfolio = 18.20%
NOTE: Higher return & Lower risk
How did we do that? DIVERSIFICATION
Слайд 21
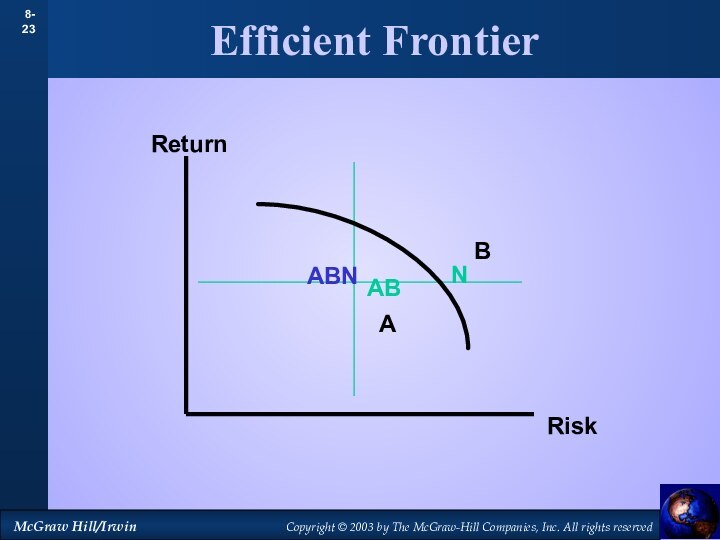
Efficient Frontier
Return
Risk
Low Risk
High Return
High Risk
High Return
Low Risk
Low Return
High
Risk
Low Return
Слайд 22
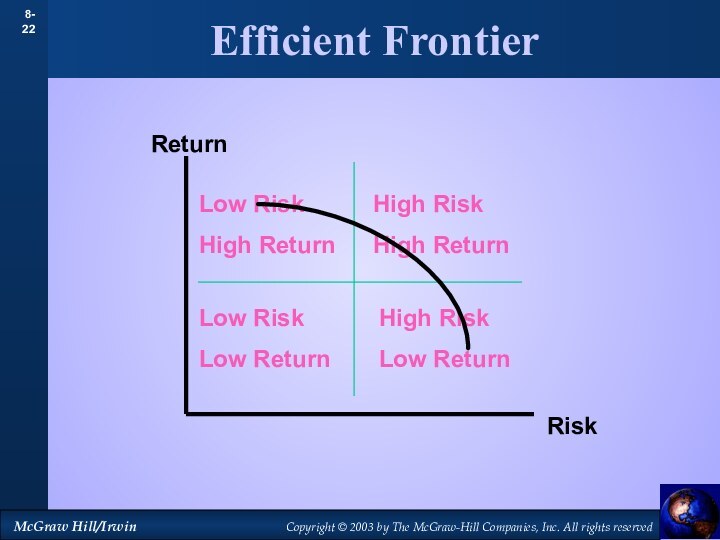
Efficient Frontier
Return
Risk
Low Risk
High Return
High Risk
High Return
Low Risk
Low Return
High
Risk
Low Return
Слайд 29
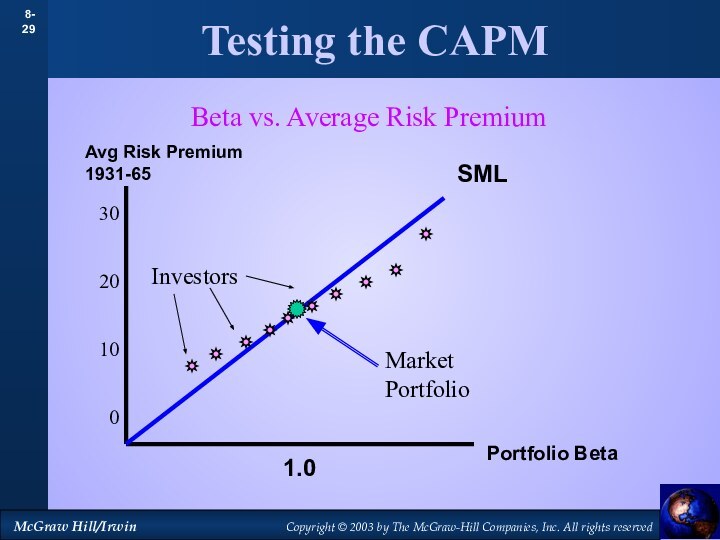
Testing the CAPM
Avg Risk Premium 1931-65
Portfolio Beta
1.0
SML
30
20
10
0
Investors
Market Portfolio
Beta
vs. Average Risk Premium
Слайд 30
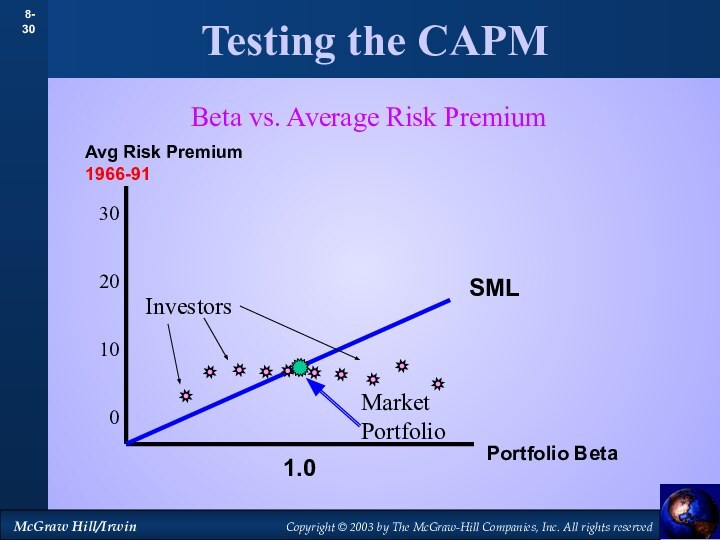
Testing the CAPM
Avg Risk Premium 1966-91
Portfolio Beta
1.0
SML
30
20
10
0
Investors
Market Portfolio
Beta
vs. Average Risk Premium
Слайд 31
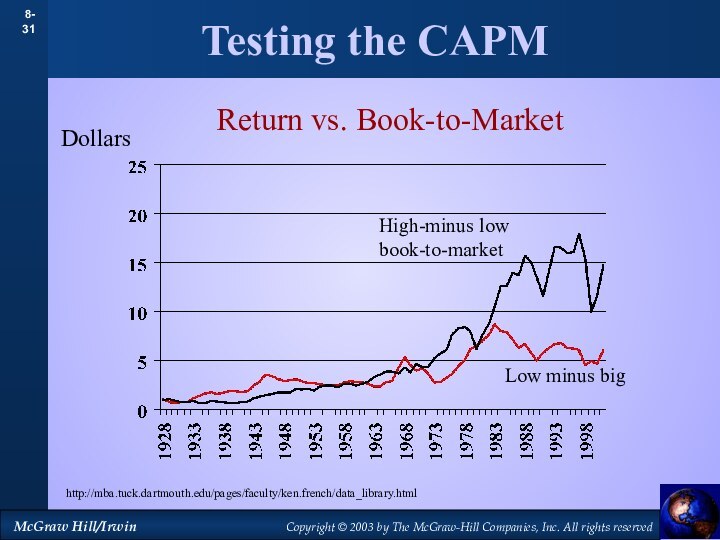
Testing the CAPM
High-minus low book-to-market
Return vs. Book-to-Market
Dollars
Low minus
big
http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html
Слайд 33
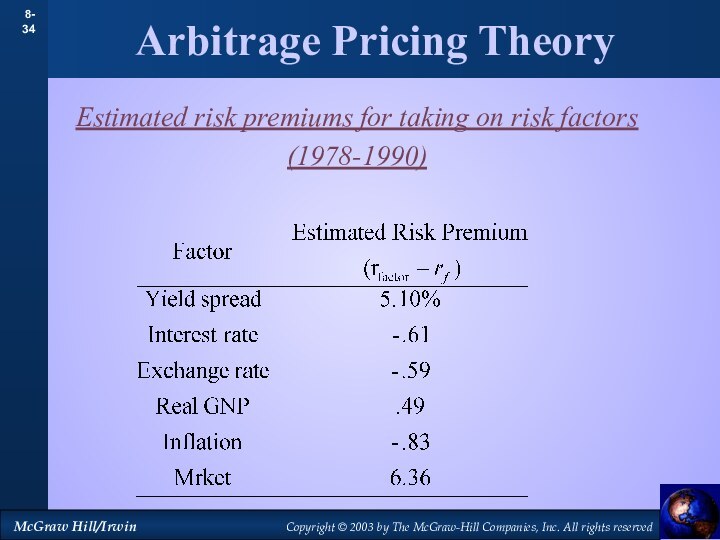
Arbitrage Pricing Theory
Alternative to CAPM
Expected Risk
Premium = r - rf
= Bfactor1(rfactor1 - rf) + Bf2(rf2 - rf) + …
Return = a + bfactor1(rfactor1) + bf2(rf2) + …