- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Средние величины
Содержание
- 2. средние величиныпредставляют собой обобщенную характеристику признака в статистической совокупности в конкретных условиях места и времени
- 3. Значимость использования средних величин СРЕДНЯЯ ВЕЛИЧИНА заменяет
- 4. принципы применения средних величин обоснованность выбора единиц
- 5. Средняя арифметическая простая Средняя арифметическая взвешеннаяСредняя гармоническаяСредняя
- 6. вычисляется, как сумма отдельных значений признака деленная
- 7. Например:Имеются данные о стаже 7 работников
- 8. вычисляется, если имеются многократные повторения значения признака
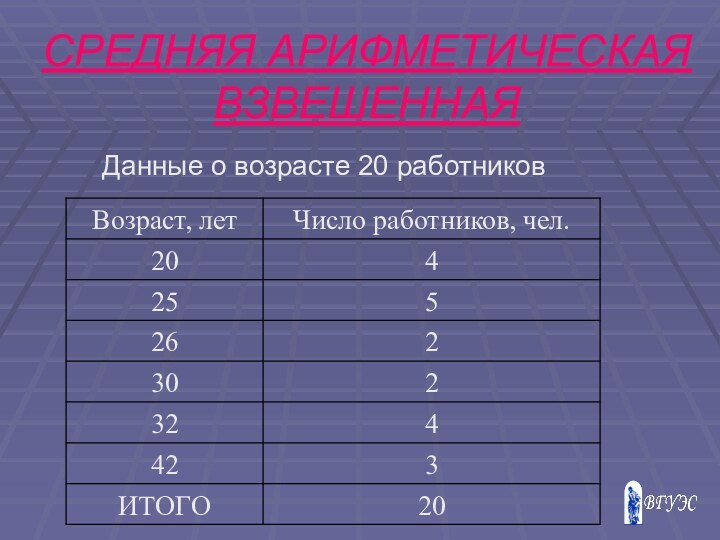
- 9. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ ВЗВЕШЕННАЯДанные о возрасте 20 работников
- 10. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ ВЗВЕШЕННАЯза х - примем признак
- 11. Рассчитывается, если отсутствуют данные о величине частот
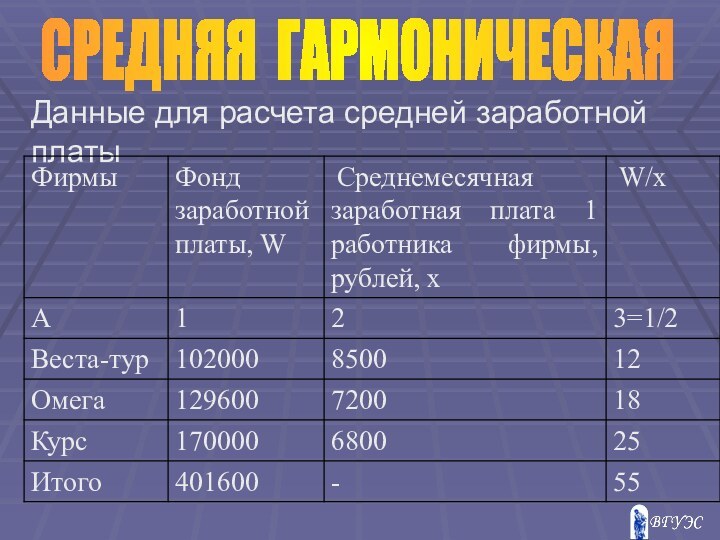
- 12. СРЕДНЯЯ ГАРМОНИЧЕСКАЯДанные для расчета средней заработной платы
- 13. СРЕДНЯЯ ГАРМОНИЧЕСКАЯТогда размер средней заработной платы одного
- 14. СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯРассчитывается, когда индивидуальные значения признаков
- 15. СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯгде n – число значений
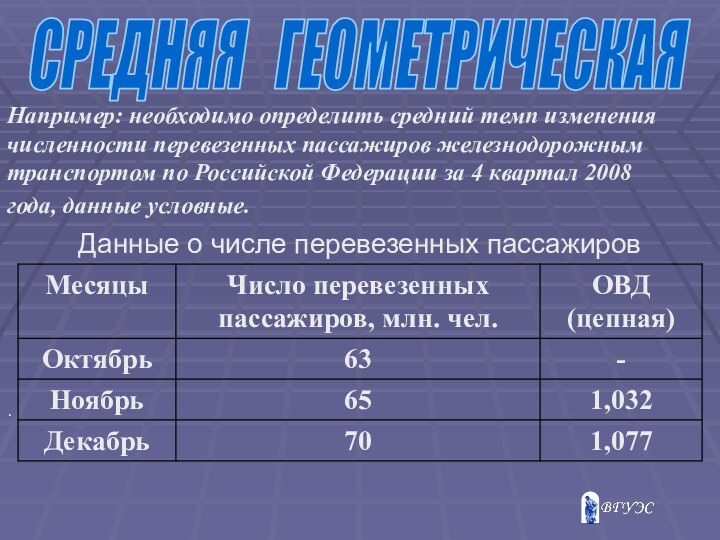
- 16. СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ. Данные о числе перевезенных
- 17. Х= √1,032*1,077= 1,054*100=105,4%Следовательно, в среднем за месяц
- 18. . исчисляется из показателей изменяющихся во времени
- 19. .
- 20. Скачать презентацию
- 21. Похожие презентации
средние величиныпредставляют собой обобщенную характеристику признака в статистической совокупности в конкретных условиях места и времени

















Слайд 2
средние величины
представляют собой обобщенную характеристику признака в статистической
совокупности в конкретных условиях места и времени
Слайд 3
Значимость использования средних величин
СРЕДНЯЯ ВЕЛИЧИНА
заменяет индивидуальные
значения варьирующего
признака единиц
наблюдения,
на усредненную
величину, достаточно
объективно
отражающую
свойства совокупности
Слайд 4
принципы применения средних величин
обоснованность выбора единиц совокупности
определение качественного содержания усредняемого
признака
учет взаимосвязи изучаемых признаков
Слайд 5
Средняя арифметическая простая
Средняя арифметическая взвешенная
Средняя гармоническая
Средняя геометрическая
Средняя хронологическая
Структурные (описательные средние) - мода, медиана
ВИДЫ СРЕДНИХ ВЕЛИЧИН
Слайд 6 вычисляется, как сумма отдельных значений признака деленная на
их число
СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ
ПРОСТАЯ
где xi - индивидуальное значение i-ого признака,
n - общий объем совокупности
Слайд 7
Например:
Имеются данные о стаже 7 работников фирмы
(лет):
15, 12, 16, 21, 11, 10, 13 .
Х = 15+12+16+21+11+10+13 = 98 =14 лет.,
7 7
Средний стаж одного работника составил 14 лет.
СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ
ПРОСТАЯ
Слайд 8 вычисляется, если имеются многократные повторения значения признака и
совокупность разбита на группы
где - Х i значения
признака в i-ой группе , fi -число повторов (частоты) в i-ой группе,
СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ
ВЗВЕШЕННАЯ
Слайд 10
СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ
ВЗВЕШЕННАЯ
за х - примем признак возраст,
за
f - количество работников определенного возраста
Х = 20*4+25*5+26*2+30*2+32*4+42*3
= 571 = 28, 55 лет20 20
средний возраст работника составляет около 29 лет.
Слайд 11 Рассчитывается, если отсутствуют данные о величине частот признака
(f), но имеются данные об индивидуальных значениях признака (x)
и величине, представляющей собой произведение признака на частоту (W =x*f). При этом неизвестное значение f легко определить как отношение W на х, то есть f= W/xгде х – отдельные варианты;
W – число вариантов
СРЕДНЯЯ ГАРМОНИЧЕСКАЯ
Слайд 13
СРЕДНЯЯ ГАРМОНИЧЕСКАЯ
Тогда размер средней заработной платы одного работника
фирмы составит
Х= 401600 = 7302 рубля
55
Слайд 14
СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ
Рассчитывается, когда индивидуальные значения признаков представлены
относительными величинами динамики (цепными), то есть когда требуется охарактеризовать
интенсивность развития явлений и процессов за длительный период..
Слайд 15
СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ
где n – число значений признака,
П – знак перемножения х
.
где
х - относительные величины динамики
Слайд 16
СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ
.
Данные о числе перевезенных пассажиров
Например:
необходимо определить средний темп изменения численности перевезенных пассажиров железнодорожным
транспортом по Российской Федерации за 4 квартал 2008 года, данные условные.
Слайд 17
Х= √1,032*1,077= 1,054*100=105,4%
Следовательно, в среднем за месяц число
перевезенных пассажиров железнодорожным транспортом в четвертом квартале 2008 года
увеличивалось на 5,4%.СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ
.
Слайд 18
.
исчисляется из показателей изменяющихся во времени и
представленных на конкретный момент времени (дату)
СРЕДНЯЯ ХРОНОЛОГИЧЕСКАЯ
где х – значение признака
n – число моментов времени
Слайд 19
.
СРЕДНЯЯ ХРОНОЛОГИЧЕСКАЯ
Например: рассчитать на начало месяца среднюю
величину остатка денежных средств на расчетном счете (за 1-ое полугодие 2008 года, данные условные)Данные об остатке денежных средств





























