- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теория производства
Содержание
- 2. Тема 4. Теория производства1. Производственная функция: понятие
- 3. 1. Производственная функция: понятие и видыПроизводство -
- 4. Технология накладывает ограничения на возможности создания товаров,
- 5. Способ производства является технологически эффективным, если:Объем произведенного
- 6. Виды производственных функцийВ зависимости от анализа влияния
- 7. Виды производственных функцийПо количеству рассматриваемых факторов:Однофакторные;Двухфакторные;Многофакторные.По эластичности
- 8. Из всевозможных производственных функций основное внимание уделяется
- 9. Для разных видов производства производственные функции различны,
- 10. 2. Однофакторная производственная функцияОднофакторная производственная функция показывает зависимость выпуска от одного переменного фактора (например, труда): Q=f(X1)
- 11. Основными показателями использования одного фактора производства являются:Общий
- 12. Производство с одним переменным фактором
- 13. Средний продукт j-го ресурса – APj (average
- 14. Предельный продукт j-го ресурса – MPj (marginal
- 15. Производство с одним переменным фактором (взаимосвязь общего,
- 16. Рассмотрим характеристики стандартной технологии с точки зрения
- 17. Свойства графика: Максимальная отдача – в
- 18. Закон убывающей предельной производительностиС ростом использования какого-либо
- 19. 3. Двухфакторная производственная функцияДвухфакторная производственная функция показывает
- 20. Изоквантакривая, которая показывает все возможные комбинации факторов,
- 21. Производство с двумя переменными факторамиK
- 22. Виды изоквант:Ресурсы абсолютно взаимодополняемые – изоквантаРесурсы абсолютно
- 23. Характеристики изокванты и производства:предельная норма технического замещение
- 24. На положение изокванты влияет:Технический прогресс обуславливает движение
- 25. 4. Равновесие производителяРавновесие производителя в однофакторной моделиQMPx
- 26. Выводы:Существует оптимальный размер производства и соответствующий ему
- 27. Если в производстве используется множество факторов, то
- 28. Равновесие производителя в двухфакторной моделиПусть заданы цена
- 29. ИзокостаИзокоста – прямая равных издержек (бюджет производителя)Уравнение
- 30. КLααβ
- 31. Решение задачи производителяЕ -точка равновесияпроизводителяK*L*LK
- 32. Равновесие в неоклассической модели единственно:
- 33. 5. Расширение производства в коротком и длительном
- 34. КLQ1Q2Q**E1E2E3L**K^Траектория расширения производства короткого периода
- 35. Длительный период – временной интервал, в рамках
- 36. Типы отдачи (производительности) от масштаба: Возрастающая отдача
- 37. КLQ1Q2Q3E1E2E3Траектория расширения производства длительного периода
- 38. Скачать презентацию
- 39. Похожие презентации





























Слайд 2
Тема 4. Теория производства
1. Производственная функция: понятие и
виды
Расширение производства в коротком и длительном периодах
Слайд 3
1. Производственная функция: понятие и виды
Производство - процесс
трансформации ресурсов, которые также называются факторами производства, на основе
определенной технологии в продукцию.Факторы производства - труд, капитал, земля, предпринимательские способности, информация…
Технология – способ преобразования факторов производства в продукт.
Производственная функция определяет объём выпуска Q, который фирма может осуществить при данной технологии и каждом конкретном сочетании факторов производства.
Слайд 4
Технология накладывает ограничения на возможности создания товаров, определяя:
Технологические
возможности и границы замещения факторов производства (определяются особенностями конкретного
технологического процесса)Экономические возможности замещения факторов производства (определяются производительностью фактора и его ценой)
Слайд 5
Способ производства является технологически эффективным, если:
Объем произведенного продукта
является максимальным при использовании данного количества факторов производства;
Для производства
заданного объема продукции использовано минимальное количество ресурсов (затраты не увеличились).
Слайд 6
Виды производственных функций
В зависимости от анализа влияния факторов
производства на объём выпуска в определённый момент времени или
в разные промежутки времени производственные функции делятся на:Статические Q = f(x1,x2,...,xn)
Динамические Q = f(x1(t),...,xk(t),...,xn).
По характеру отражаемой связи выделяют:
Линейные
Q = a1x1 + a2x2 + … + anxn
Мультипликативно-степенные
Q = A·x1a1·x2a2· … ·xnan
Такие производственные функции при отсутствии одного из факторов обращаются в ноль.
Слайд 7
Виды производственных функций
По количеству рассматриваемых факторов:
Однофакторные;
Двухфакторные;
Многофакторные.
По эластичности замещения
ресурсов:
с постоянной эластичностью замены (CES — Constant Elasticity of Substitution)
Q = A [(1
– α) K-b + αL-b]-c/bС переменной эластичностью, т. е. зависимой от объемов ресурсов (VES — Variable Elasticity of Substitution)
Слайд 8 Из всевозможных производственных функций основное внимание уделяется функциям
с неоклассическими свойствами:
Если x=0, следовательно Q=0;
Функция должна
быть дважды дифференцируема; Предельный продукт фактора (MPx) положителен:
Убывающая отдача дополнительных затрат фактора:
Слайд 9 Для разных видов производства производственные функции различны, тем
не менее все они имеют общие свойства. Можно выделить
два основных свойства:Существует предел для роста объема выпуска, который может быть достигнут ростом затрат одного ресурса при прочих равных условиях.
Существует определенная взаимная дополняемость (комплементарность) факторов производства, однако без уменьшения объема выпуска вероятна и определенная взаимозаменяемость данных факторов производства.
Слайд 10
2. Однофакторная производственная функция
Однофакторная производственная функция показывает зависимость
выпуска от одного переменного фактора (например, труда):
Q=f(X1)
Слайд 11
Основными показателями использования одного фактора производства являются:
Общий продукт
j-го ресурса – TPj (total product) – объем выпуска,
обеспеченный общим объемом ресурса j-го вида при фиксированных объемах использования других ресурсов. Общий продукт показывает эффект от использования j-го ресурса в производстве.Величина общего продукта определяется следующим образом: TPj(Хj) = Q(Хj,Х1,Х2,…Хj-1,Хj+1,…Хm) – Q(0,Х1,Х2,…Хj-1,Хj+1,…Хm) = = Q(Хj,Х^) – Q(0,Х^), где Х^ = (Х1^,Х2^,…Хj-1^,Хj+1^,…Хm^) – вектор затрат ресурсов размерностью (m-1).
По мере увеличения затрат ресурса TPj возрастает, если не происходит «перенасыщения» производственного процесса переменным фактором (фактор не становится абсолютно избыточным). При любых объемах использования переменного фактора положительны: TPj > 0.
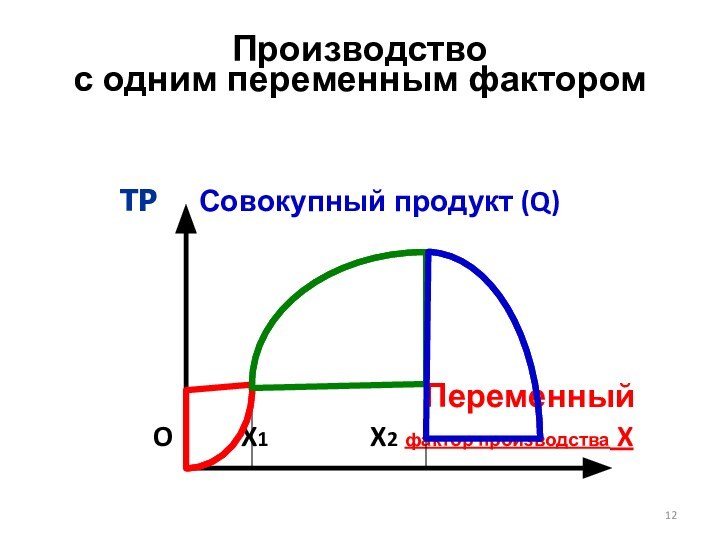
Слайд 12
Производство
с одним переменным фактором
TP Совокупный продукт (Q)
ПеременныйO X1 X2 фактор производства X
Слайд 13 Средний продукт j-го ресурса – APj (average product)
– объем выпуска, обеспеченный каждой использованной единицей ресурса j-го
вида при фиксированных объемах использования других ресурсов.Средний продукт показывает эффективность в производственном процессе каждой использованной единицы ресурса.
Величина среднего продукта ресурса вида j определяется так: APj (Хj) = TPj / Хj = Q(Хj,Х^) / Хj > 0.
Величина среднего продукта ресурса, как правило, изменяется при увеличении (уменьшении) объемов его использования ⇒ необходимость анализа динамики APj.
Слайд 14 Предельный продукт j-го ресурса – MPj (marginal product)
– объем выпуска, обеспеченный дополнительной единицей ресурса j-го вида
при фиксированных объемах использования других ресурсов.Предельный продукт ресурса показывает эффективность использования в производстве дополнительной единицы ресурса.
Величина предельного продукта ресурса вида j определяется: MPj(Хj) = ∂TPj / ∂Хj = ∂Q(Хj,Х^) /∂Хj - для непрерывных функций MPj(Хj) = TPj(Хj) –TPj(Хj-1) = Q(Хj,Х^) –Q(Хj-1,Х^) - для дискретных функций
Динамика предельного продукта: MPj ≥ 0, если ресурс не является абсолютно избыточным. MPj = 0 - в «точке насыщения» . MPj < 0, если ресурс стал абсолютно избыточным.
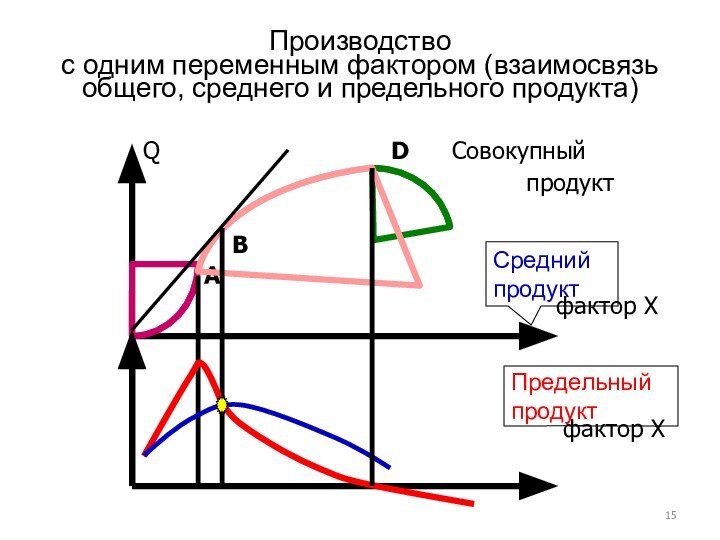
Слайд 15 Производство с одним переменным фактором (взаимосвязь общего, среднего и
предельного продукта)
Q
D Совокупныйпродукт
B
А
фактор Х
фактор Х
Средний
продукт
Предельный
продукт
Слайд 16 Рассмотрим характеристики стандартной технологии с точки зрения последовательных
затрат фактора
На интервале (1) каждая последовательная единица фактора дает
нам все большую отдачу, следовательно, предельная производительность растет, а с ней растет и AP, вплоть до точки А.На участке (2) каждая последующая единица дает все меньшую отдачу, но, тем не менее, отдача каждой следующей единицы все еще выше, чем средняя отдача всех предшествующих затрат, следовательно, АР растет, вплоть до точки В. Отдача от дополнительной единицы факторов в точке В равна отдаче от всех предшествующих затрат, следовательно, АР = МР.
На участке (3) каждая дополнительная единица фактора дает меньше отдачи, чем в среднем все предшествующие, поэтому понижение МР ведет к снижению АР до точки D. После точки D новые затраты фактора дают нулевой эффект.
Слайд 17
Свойства графика:
Максимальная отдача – в точке А.
Максимальная
средняя отдача – в точке В.
Максимальный выпуск продукции
– в точке D.
Слайд 18
Закон убывающей предельной производительности
С ростом использования какого-либо фактора
производства (при неизменности остальных) достигается точка, в которой дополнительное
применение переменного фактора ведет к снижению относительного и далее абсолютного объёмов выпуска продукции.
Слайд 19
3. Двухфакторная производственная функция
Двухфакторная производственная функция показывает максимально
возможный объем выпуска продукции при использовании двух факторов производства:
труда и капитала.Можно представить в следующем виде: Q = f(L,K) при этом:
Q(0,L) = Q(K,0) = 0;
Труд и капитал являются взаимозаменяемыми факторами производства и одновременно взаимодополняемыми
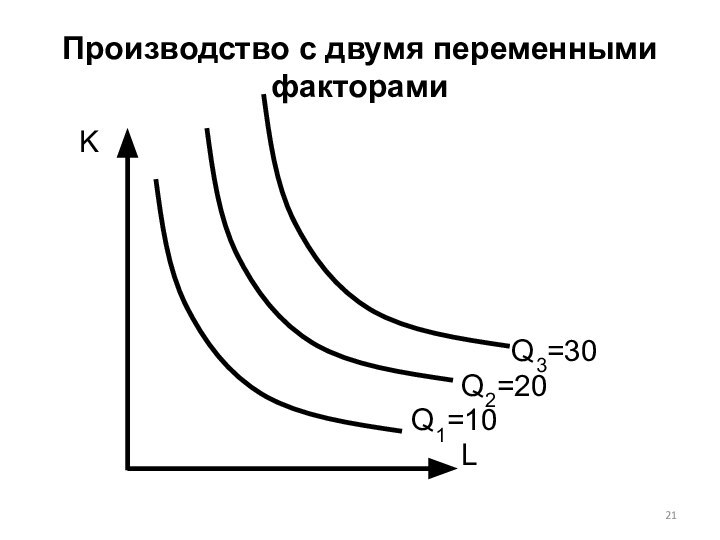
Слайд 20
Изокванта
кривая, которая показывает все возможные комбинации факторов, обеспечивающие
одинаковый объём выпуска продукции;
карта изоквант описывает производственную функцию
фирмы;изокванта дает информацию о технологии производства.
для одной и той же технологии изокванты не пересекаются;
для неоклассической производственной функции изокванты не пересекают оси координат.
чем больше выпуск Q, тем изокванта дальше от начала координат;
если мы движемся по изокванте, мы можем рассмотреть возможности взаимной замены ресурсов при постоянном выпуске Q в условиях данной технологии.
Слайд 22
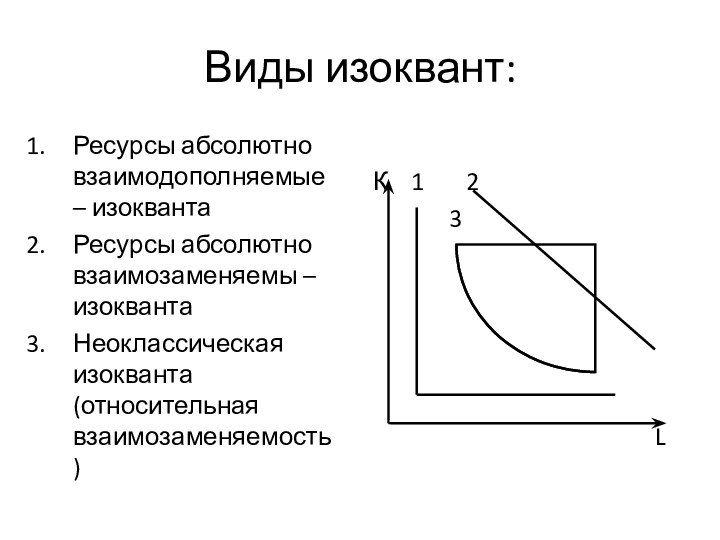
Виды изоквант:
Ресурсы абсолютно взаимодополняемые – изокванта
Ресурсы абсолютно взаимозаменяемы
– изокванта
Неоклассическая изокванта (относительная взаимозаменяемость)
К 1 2
3
L
Слайд 23
Характеристики изокванты и производства:
предельная норма технического замещение (MRTS)
показывает возможности замещения ресурсов в каждой точке. Показатель MRTS
должен быть связан с МР:степень изогнутости изокванты определяется эластичностью взаимной замены факторов. Эластичность этой функции будет показывать, на сколько процентов изменится K/L, если MRTS изменится на 1%.
Слайд 24
На положение изокванты влияет:
Технический прогресс обуславливает движение по
изокванте в условиях неизменной технологии (например, механизация)
Технологический прогресс вызывает
изменение изокванты
Слайд 25
4. Равновесие производителя
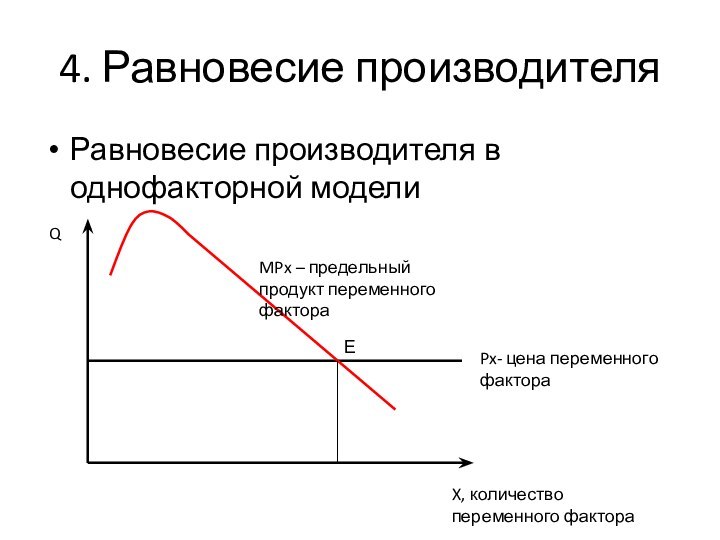
Равновесие производителя в однофакторной модели
Q
MPx –
предельный продукт переменного фактора
Px- цена переменного фактора
X, количество переменного
фактораЕ
Слайд 26
Выводы:
Существует оптимальный размер производства и соответствующий ему объем
затрат факторов;
Условие выбора оптимального количества факторов является равенство предельного
продукта в денежном выражении (MPx*PQ) и цены переменного фактора (Px), что графически отражает точка Е:PQ*MPx = Px
Это означает, что производство будет расширяться до тех пор, пока выгода от привлечения дополнительного переменного фактора не сравняется с издержками его привлечения.
Слайд 27 Если в производстве используется множество факторов, то последняя
единица денег потраченная фирмой на приобретение каждого фактора должна
давать одинаковый эффект по каждому фактору:
Слайд 28
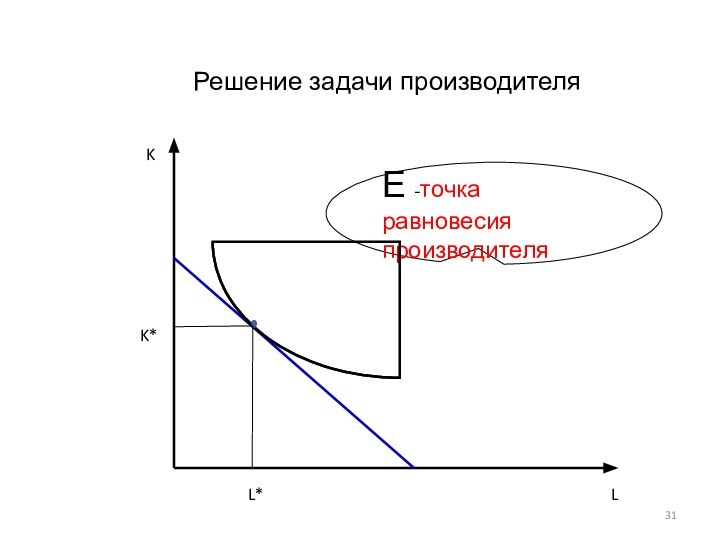
Равновесие производителя в двухфакторной модели
Пусть заданы цена товара
(PQ), цены факторов производства (PL и PK соответственно), известна
технология (т.е. известны изокванты).Задача производителя: найти оптимальный объем выпуска и соотношение затрат факторов при данном уровне бюджета фирмы.
Слайд 29
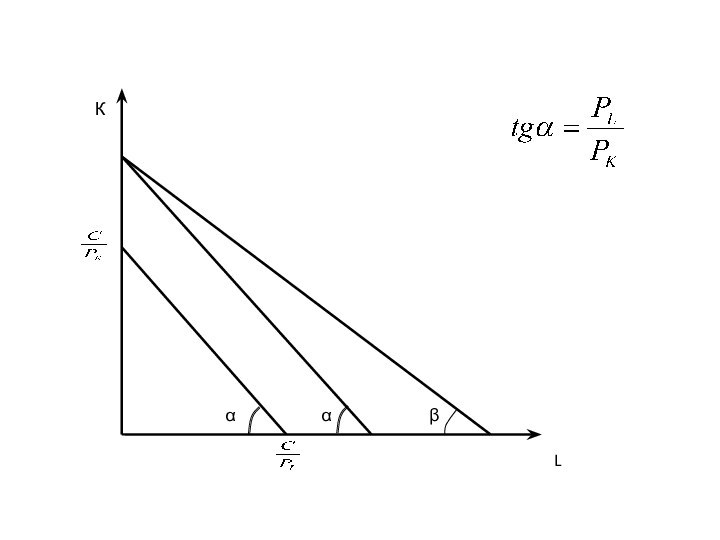
Изокоста
Изокоста – прямая равных издержек (бюджет производителя)
Уравнение изокосты:
TC = Pk x K + Pl x L,
гдеTC - издержки фирмы
Pk - цена единицы капитала
Pl - цена единицы труда
K - количество единиц используемого капитала
L - количество единиц используемого труда
При повышении или понижении отношения изокоста параллельно сдвигается.
При изменении цен угол наклона изокосты меняется.
Слайд 33
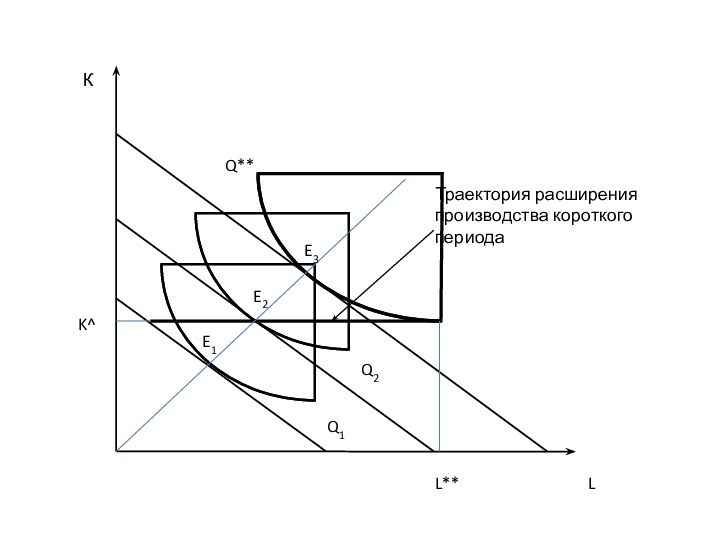
5. Расширение производства в коротком и длительном периодах
Короткий
период – временной интервал, в рамках которого производитель (объективно)
не может изменить объемы использования некоторых факторов производства. Эти факторы являются постоянными.Увеличение выпуска в коротком периоде происходит за счет увеличения затрат переменных факторов, как правило, переменного фактора «труд» и постоянного фактора «капитал» в объеме K^.
Объем выпуска в коротком периоде ограничен и составляет:
Q** = F(L**, K^)
Траектория расширения производства (траектория роста, «путь развития») короткого периода – совокупность комбинаций ресурсов, применяемых для обеспечения выпуска на различном уровне в рамках короткого временного интервала.
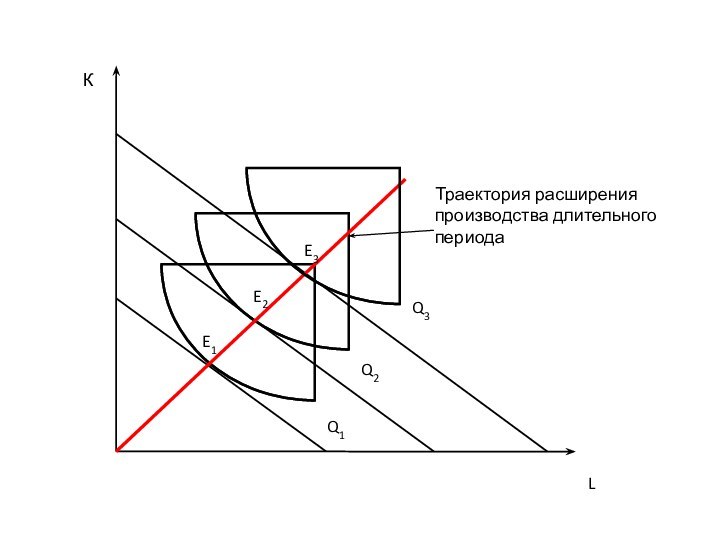
Слайд 35 Длительный период – временной интервал, в рамках которого
производитель имеет возможность варьировать затраты всех без исключения ресурсов,
в том числе – элементов основного капитала.В рамках длительного периода всегда формируются оптимальные комбинации ресурсов. Особенность длительного периода – варьируется масштаб производства - пропорциональные изменения затрат всех ресурсов в оптимальной комбинации.
Масштаб производства (ω) – коэффициент, в соответствии с которым происходит пропорциональное изменение затрат ресурсов (комбинации ресурсов – оптимальные).
Отдача от масштаба (Ω) – коэффициент, который показывает: во сколько раз изменился объем выпуска вследствие изменения масштаба производства (ω).
Эффект масштаба – изменение объема выпуска вследствие пропорционального изменения затрат всех ресурсов.
Траектория расширения производства (траектория роста, «путь развития») длительного периода – совокупность комбинаций ресурсов, применяемых для обеспечения выпуска на разном уровне в рамках длительного временного интервала.
Слайд 36
Типы отдачи (производительности) от масштаба:
Возрастающая отдача (производительность)
от масштаба (IRS - Increasing Returns to Scale): выпуск
меняется в большей пропорции, чем затраты факторов производства: Ω > ω.Постоянная отдача (производительность) от масштаба (CRS - Constant Returns to Scale ): выпуск меняется в такой же пропорции, что и затраты факторов производства: Ω = ω.
Убывающая отдача (производительность) от масштаба (DRS - Decreasing Returns to Scale ): выпуск меняется в меньшей пропорции, чем затраты факторов производства: Ω < ω.