q, r, s, t, p1,q1,…
Логические союзы (пропозициональные связки)
Технические знаки – (, ).А.И.Мигунов
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





















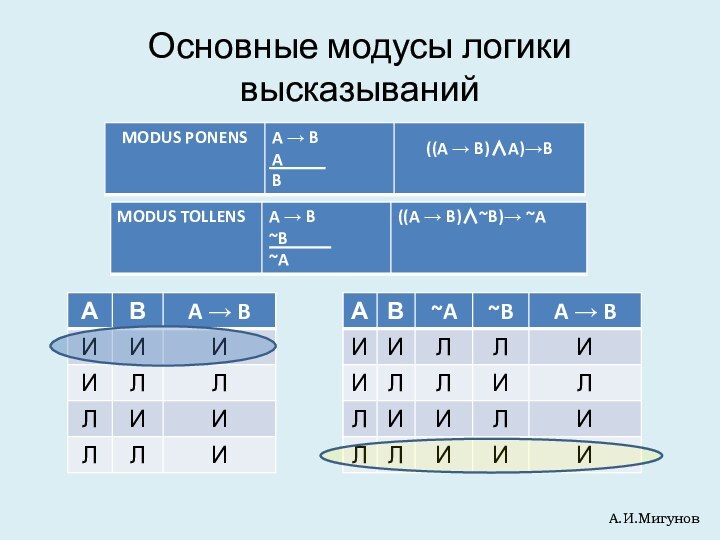









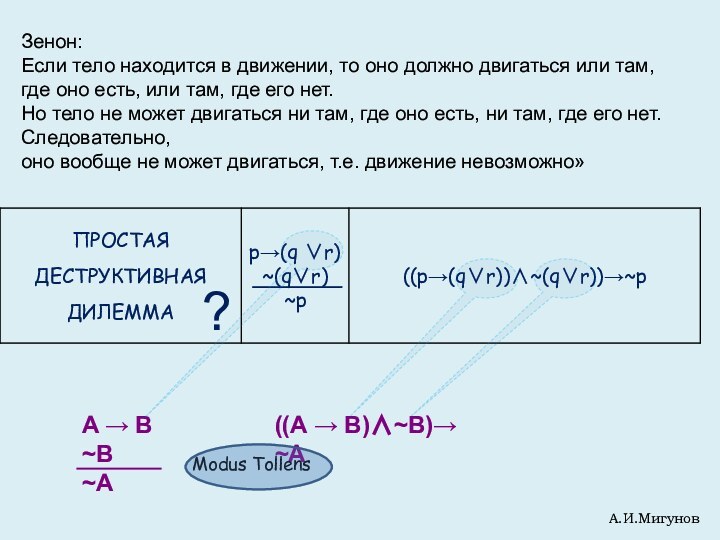
А.И.Мигунов
А.И.Мигунов
(B ∨ C)
((A → B) ∧ A) → (B ∨ C)
А.И.Мигунов
∨
∧
→
(
)
(
)
~А
∧
В
А.И.Мигунов
Принцесса в комнате 1 - p1
Принцесса в комнате 2 - p2
Тигр в комнате 1 - t1
(p1 v p2) t1
↔
А.И.Мигунов
p → q
~q
~p
А1, А2├ В
А.И.Мигунов
А.И.Мигунов
Формула логики высказываний является тождественно-истинной формулой,
если при любых интерпретациях вхордящих в ее состав пропозициональных
переменных она принимает значение «истина».
А1, А2├ В
(А1 ∧ А2)→ В
((p → q)∧~q)→ ~p
А.И.Мигунов
Я плачу за работу по ремонту телевизора – p
Телевизор работает - r
((r → p) ∧ ~ r) → ~ p
А.И.Мигунов