сохраняют свои свойства при непрерывных деформациях, таких, например, как
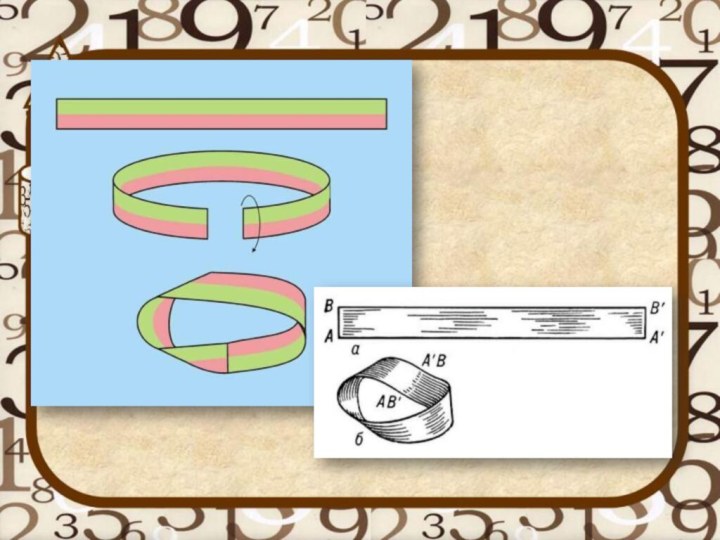
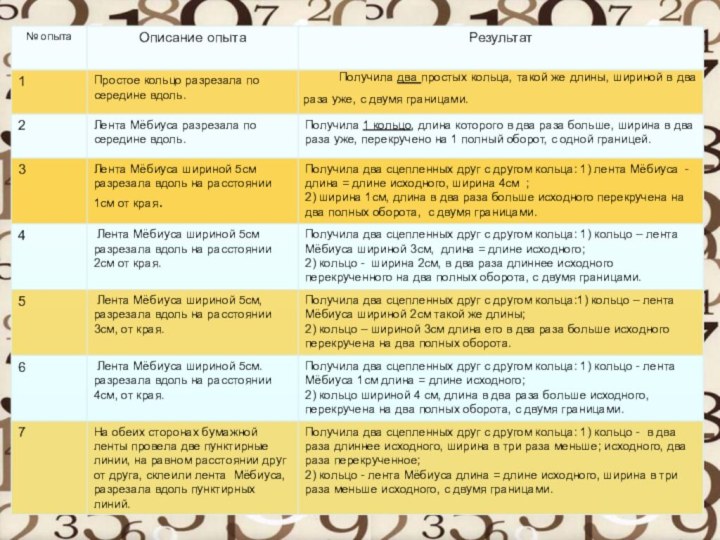
растяжение, сжатие или изгибание.Лист Мёбиуса является топологическим, то есть непрерывным объектом с
простейшей односторонней поверхностью с границей в обычном Евклидовом пространстве (3-мерном), где возможно из одной точки такой поверхности, не пересекая края, попасть в любую другую.