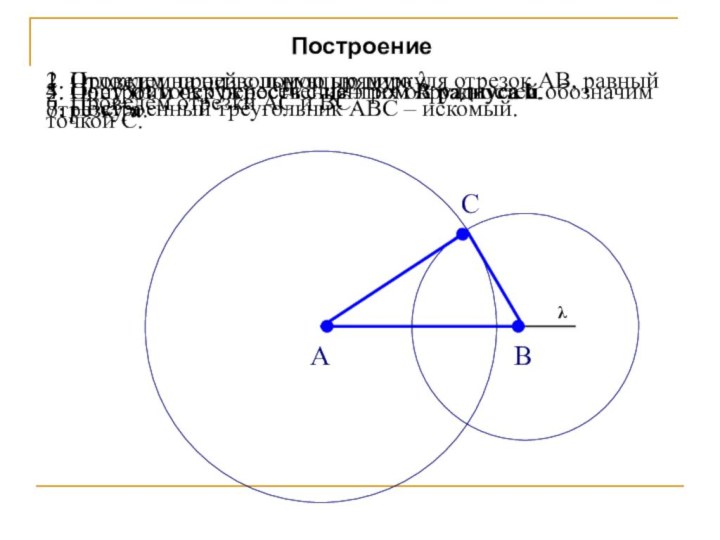
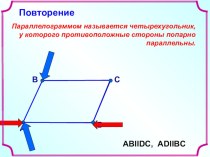
указывающее, по каким данным, какими средствами (инструментами) и какой
геометрический образ (точку, прямую, окружность, треугольник, совокупность точек и т. д.) требуется найти (начертить, построить на плоскости, наметить на местности и т. п.) так, чтобы этот образ удовлетворял определенным условиям» (Басова Л. А.)«Задача на построение – это своеобразная теорема, которая отвечает на вопрос, каким образом выполнять построения в любом из возможных случаев, и сколько решений при этом может оказаться» (Волович М. Б.)