- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение задний В9
Содержание
- 2. *№1. Площадь поверхности куба равна 18. Найдите его диагональ АВСDA1B1C1D1Пусть ребро куба равно а.
- 3. № 2. Во сколько раз увеличится площадь
- 4. № 3. Если каждое ребро куба увеличить
- 5. № 4. Ребра прямоугольного параллелепипеда, выходящие из
- 6. № 5. Два ребра прямоугольного параллелепипеда, выходящие
- 7. № 6. Найдите боковое ребро правильной четырехугольной
- 8. № 7. Основанием прямой треугольной призмы служит
- 9. № 8. Найдите площадь боковой поверхности правильной
- 10. № 9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).Ответ: 48
- 11. № 10. Радиус основания цилиндра равен 2, высота
- 12. № 11. Правильная четырехугольная призма описана около
- 13. № 12. Найдите площадь боковой поверхности правильной
- 14. Найдите площадь боковой поверхности правильной шестиугольной призмы,
- 15. № 14. Найдите площадь боковой поверхности правильной
- 16. Скачать презентацию
- 17. Похожие презентации
*№1. Площадь поверхности куба равна 18. Найдите его диагональ АВСDA1B1C1D1Пусть ребро куба равно а.


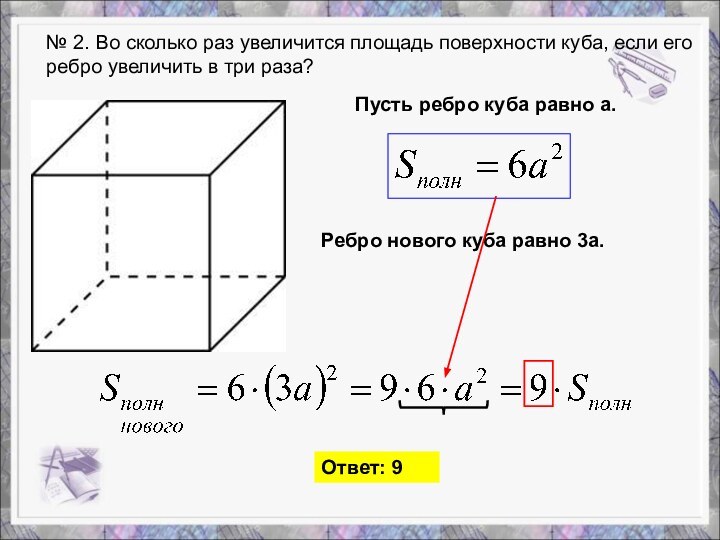











Слайд 3 № 2. Во сколько раз увеличится площадь поверхности
куба, если его ребро увеличить в три раза?
Пусть ребро
куба равно а.Ребро нового куба равно 3а.
Ответ: 9
Слайд 4 № 3. Если каждое ребро куба увеличить на
1, то его площадь поверхности увеличится на 54. Найдите
ребро куба.Пусть ребро куба равно а.
Ребро нового куба равно а+1.
Ответ: 4
Слайд 5 № 4. Ребра прямоугольного параллелепипеда, выходящие из одной
вершины, равны 1, 2, 3. Найдите его площадь поверхности.
Ответ: 22
Слайд 6 № 5. Два ребра прямоугольного параллелепипеда, выходящие из
одной вершины, равны 3 и 4. Площадь поверхности этого
параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.Слайд 7 № 6. Найдите боковое ребро правильной четырехугольной призмы,
если сторона ее основания равна 20, а площадь поверхности
равна 1760.Слайд 8 № 7. Основанием прямой треугольной призмы служит прямоугольный
треугольник с катетами 6 и 8, высота призмы равна
10. Найдите площадь ее поверхности.Ответ: 288
Слайд 9 № 8. Найдите площадь боковой поверхности правильной шестиугольной
призмы, сторона основания которой равна 5, а высота — 10.
Ответ:
300Слайд 10 № 9. Найдите площадь поверхности многогранника, изображенного на
рисунке (все двугранные углы прямые).
Ответ: 48
Слайд 11 № 10. Радиус основания цилиндра равен 2, высота равна
3. Найдите площадь боковой поверхности цилиндра, деленную на
Ответ:
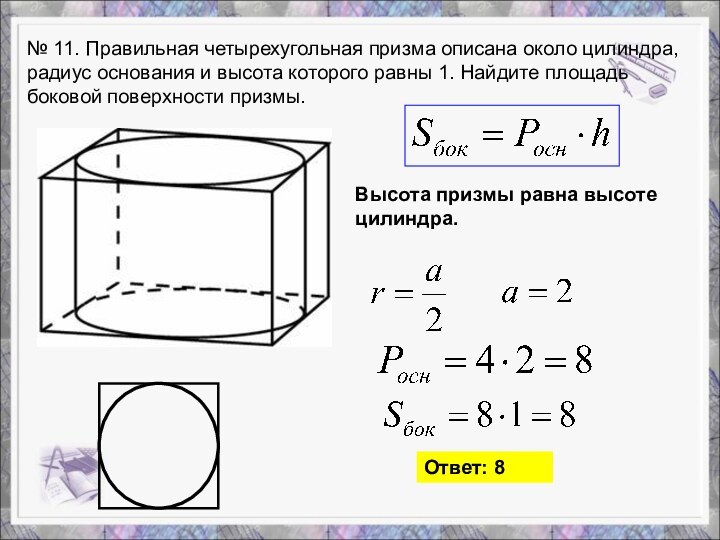
12Слайд 12 № 11. Правильная четырехугольная призма описана около цилиндра,
радиус основания и высота которого равны 1. Найдите площадь
боковой поверхности призмы.Высота призмы равна высоте цилиндра.
Ответ: 8
Слайд 13 № 12. Найдите площадь боковой поверхности правильной треугольной
призмы, описанной около цилиндра, радиус основания которого равен
,а высота равна 2.
Высота призмы равна высоте цилиндра.
Ответ: 36
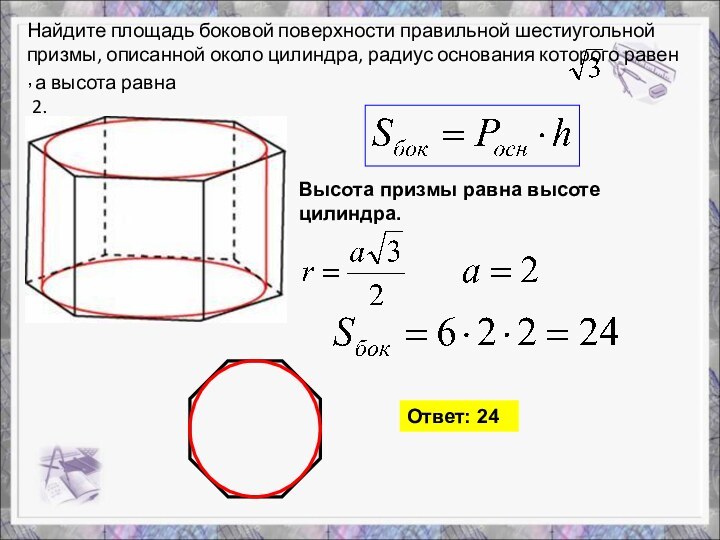
Слайд 14 Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной
около цилиндра, радиус основания которого равен
, а высота равна 2.
Высота призмы равна высоте цилиндра.
Ответ: 24
Слайд 15 № 14. Найдите площадь боковой поверхности правильной треугольной
призмы, вписанной в цилиндр, радиус основания которого равен
, а
высота равна 2.Высота призмы равна высоте цилиндра.
Ответ: 36