- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Следствия из аксиом стереометрии
Содержание
- 2. Аксиома 1Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.ABC
- 3. Аксиома 2 Если две точки прямой лежат
- 4. Аксиома 3 Если две плоскости имеют общую
- 5. 1. Как можно проверить качество изготовления
- 6. 3. Могут ли две различные плоскости, иметь,
- 10. Следствия из аксиом1. Через прямую и не
- 11. Следствия из аксиом2. Через две пересекающиеся прямые проходит плоскость и притом только однаabMN
- 12. Физкультминутка
- 14. Столяр с помощью двух нитей проверяет, будет
- 15. Задача ABCD – ромб, О – точка
- 16. Задача пересечение двух плоскостей ABCDA1B1C1D1 – куб,
- 17. Задача Дан тетраэдр МАBC, каждое ребро которого
- 18. Домашнее задание: § 3, стр.37, (отв.на вопр.1
- 19. Способы существования плоскости
- 20. Скачать презентацию
- 21. Похожие презентации













Слайд 2
Аксиома 1
Через любые три точки, не лежащие на
одной прямой, проходит плоскость, и притом только одна.
Слайд 3
Аксиома 2
Если две точки прямой лежат в
плоскости, то все точки прямой лежат в этой плоскости.
A
B
Слайд 4
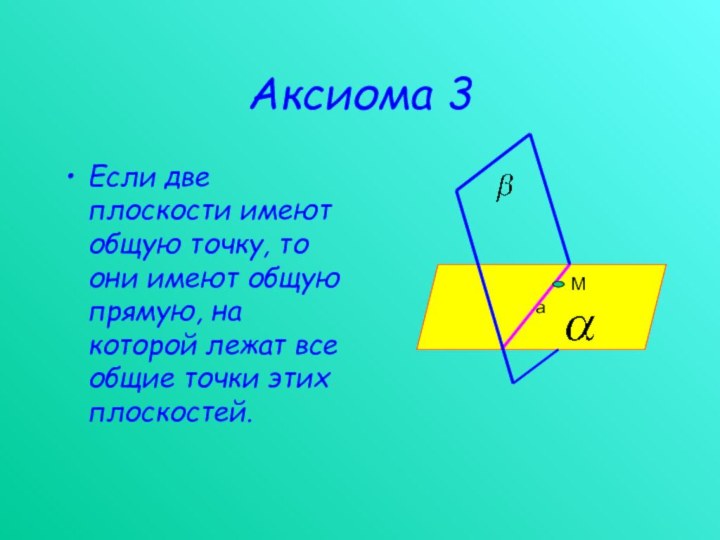
Аксиома 3
Если две плоскости имеют общую точку,
то они имеют общую прямую, на которой лежат все
общие точки этих плоскостей.a
М
Слайд 5
1. Как можно проверить качество изготовления линейки,
имея хорошо обработанную плоскую плиту? На каком теоретическом положении обоснована
эта проверка?
2. Объясните, почему стул, имеющий три ножки, обязательно устойчив, а по отношению к стулу с четырьмя ножками этого утверждать нельзя?
Слайд 6
3. Могут ли две различные плоскости, иметь, две
различные общие прямые?
4. Сколько различных плоскостей можно провести:
Через одну точку?
Через две различные точки?
Через три различные точки?
Слайд 10
Следствия из аксиом
1. Через прямую и не лежащую
на ней точку проходит плоскость и притом только одна
А
b
T
C
Слайд 11
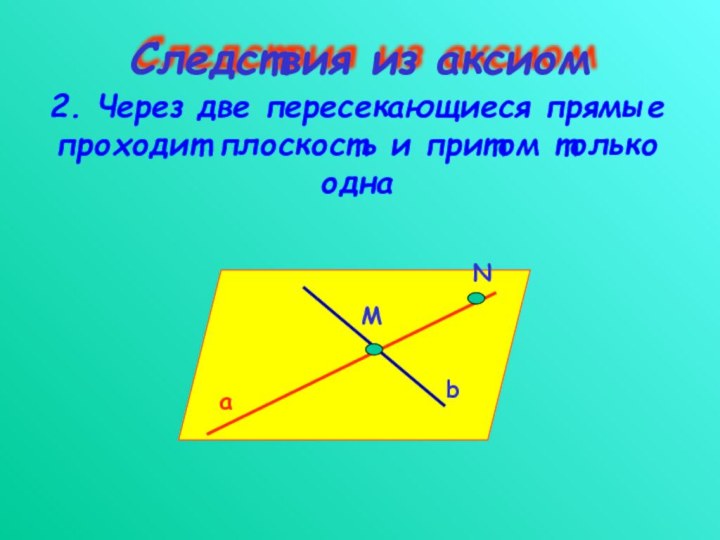
Следствия из аксиом
2. Через две пересекающиеся прямые проходит
плоскость и притом только одна
a
b
M
N
Слайд 14 Столяр с помощью двух нитей проверяет, будет ли
устойчиво стоять на полу изготовленный стол, имеющий четыре ножки.
Как нужно натянуть нити?Даны две пересекающиеся прямые. Верно ли утверждение, что любая прямая, пересекающая обе данные прямые, лежит с ними в одной плоскости?
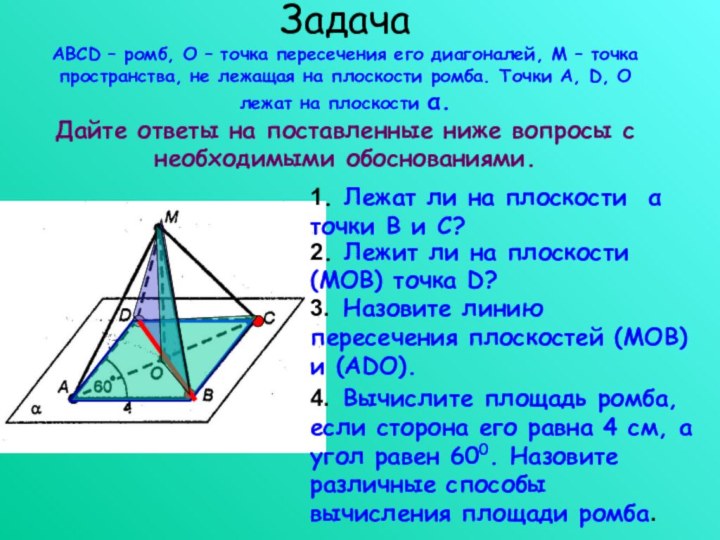
Слайд 15 Задача ABCD – ромб, О – точка пересечения его
диагоналей, М – точка пространства, не лежащая на плоскости
ромба. Точки A, D, O лежат на плоскости α. Дайте ответы на поставленные ниже вопросы с необходимыми обоснованиями.1. Лежат ли на плоскости α точки В и С?
2. Лежит ли на плоскости (МОВ) точка D?
3. Назовите линию пересечения плоскостей (МОВ) и (ADO).
4. Вычислите площадь ромба, если сторона его равна 4 см, а угол равен 600. Назовите различные способы вычисления площади ромба.
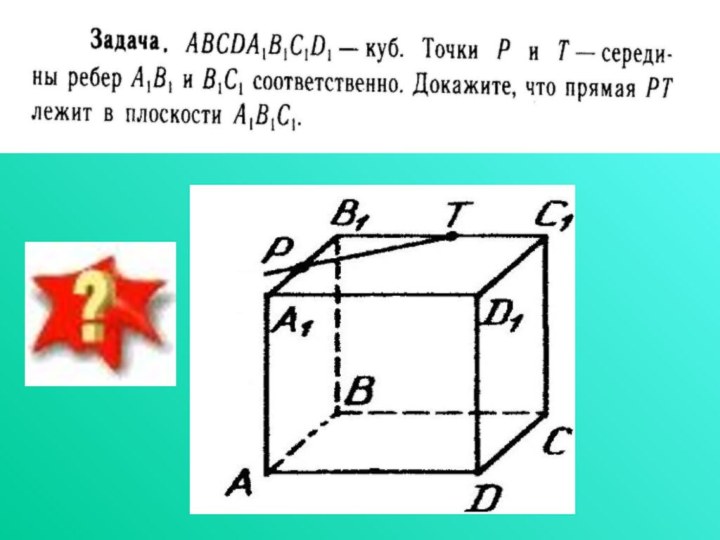
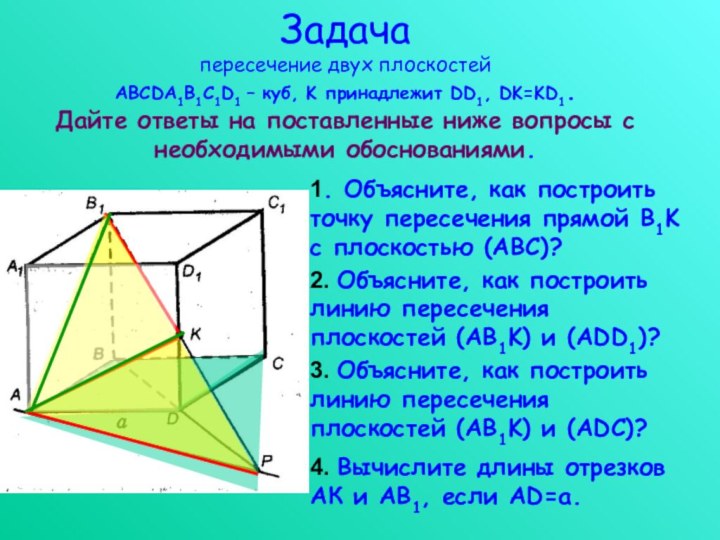
Слайд 16 Задача пересечение двух плоскостей ABCDA1B1C1D1 – куб, K принадлежит DD1,
DK=KD1.
Дайте ответы на поставленные ниже вопросы с необходимыми обоснованиями.
1.
Объясните, как построить точку пересечения прямой B1K с плоскостью (АВС)?2. Объясните, как построить линию пересечения плоскостей (AB1K) и (ADD1)?
3. Объясните, как построить линию пересечения плоскостей (AB1K) и (ADС)?
4. Вычислите длины отрезков АК и АВ1, если АD=a.
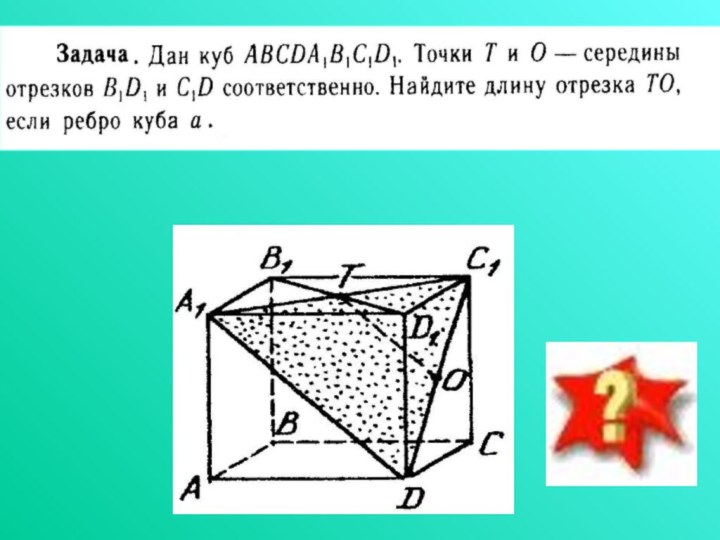
Слайд 17
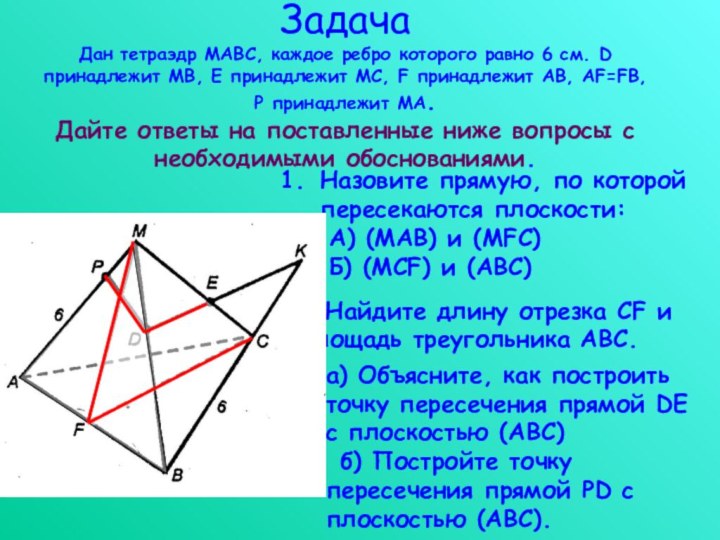
Задача
Дан тетраэдр МАBC, каждое ребро которого равно 6
см. D принадлежит МВ, Е принадлежит МС, F принадлежит
АВ, AF=FB, P принадлежит МА. Дайте ответы на поставленные ниже вопросы с необходимыми обоснованиями.Назовите прямую, по которой пересекаются плоскости:
А) (МАВ) и (MFC)
Б) (MCF) и (АВС)
2. Найдите длину отрезка CF и площадь треугольника АВС.
а) Объясните, как построить точку пересечения прямой DE с плоскостью (АВС)
б) Постройте точку пересечения прямой PD с плоскостью (АВС).
Слайд 18
Домашнее задание:
§ 3, стр.37, (отв.на вопр.1 -4),
№№ 6, 11, найти практическое применение
аксиом стереометрии и
их следствий в жизни