- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Электронный урок по теме: Теорема Пифагора
Содержание
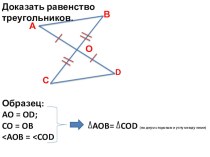
- 2. Приветствую вас на уроке геометрии в 8 классе Уроки №30-3017.12.2019 г.
- 3. Успешного усвоения материала Интересные
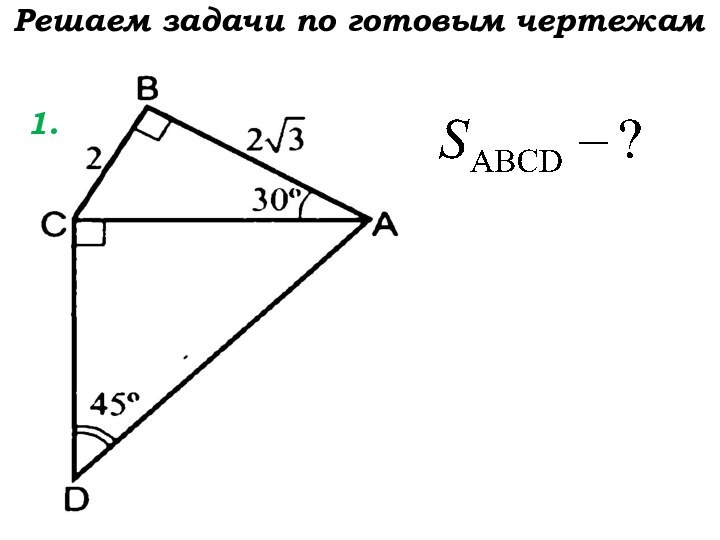
- 4. Решаем задачи по готовым чертежам 1.
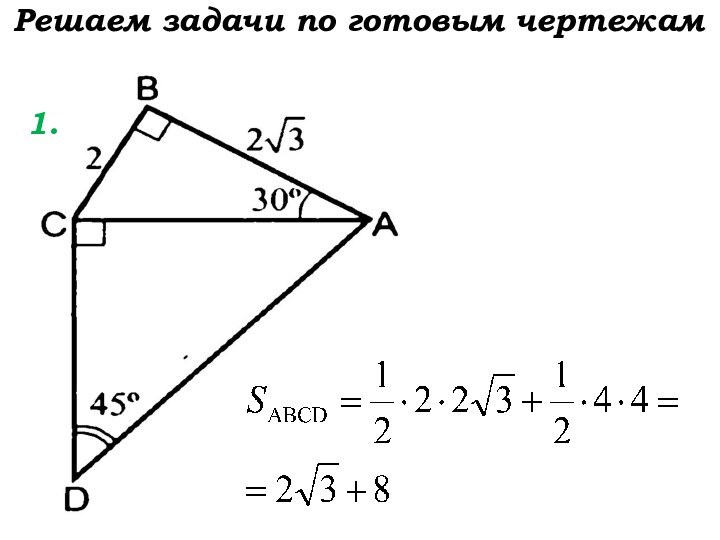
- 5. Решаем задачи по готовым чертежам 1.
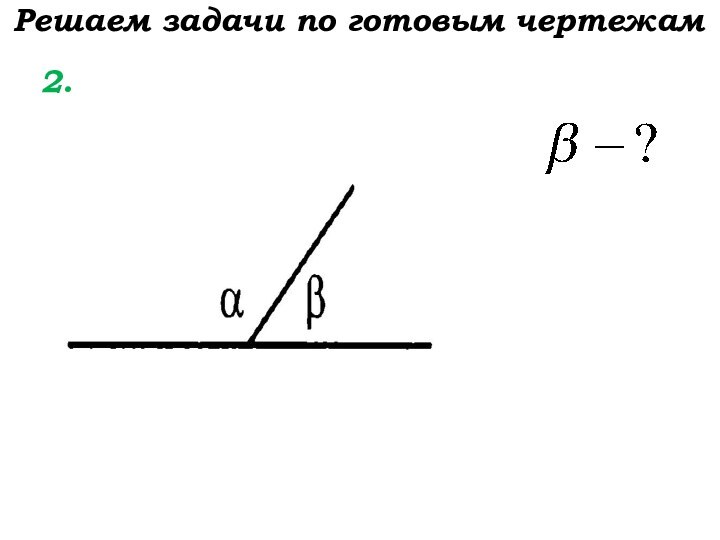
- 6. Решаем задачи по готовым чертежам 2.
- 7. Решаем задачи по готовым чертежам 2.
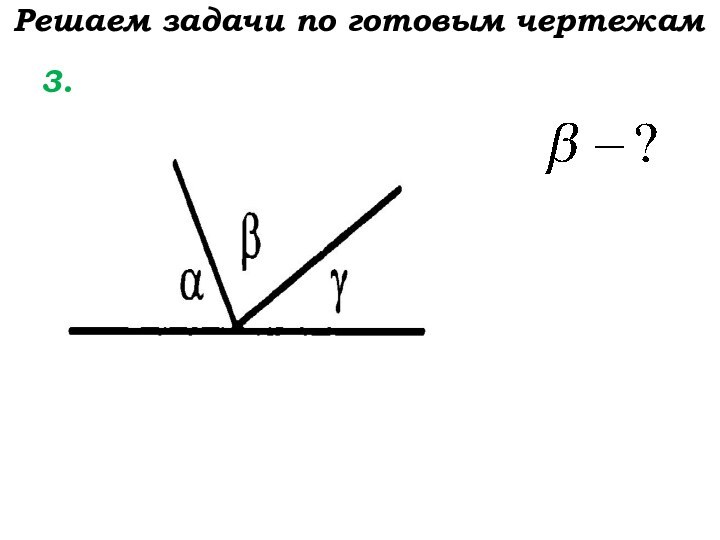
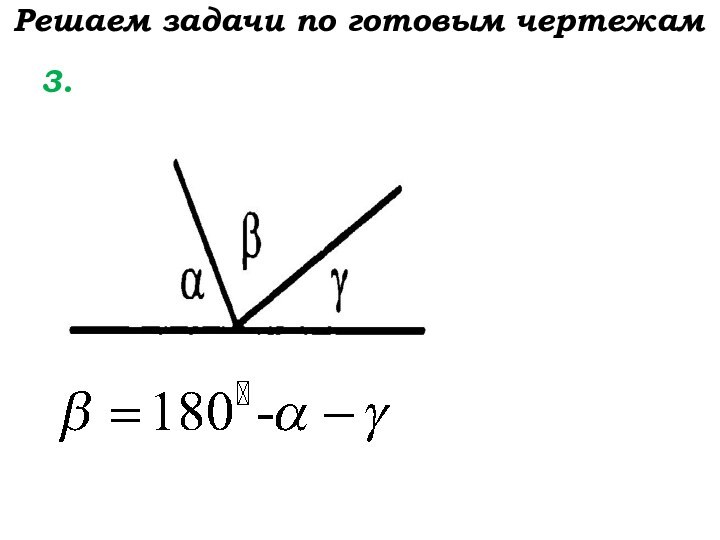
- 8. Решаем задачи по готовым чертежам 3.
- 9. Решаем задачи по готовым чертежам 3.
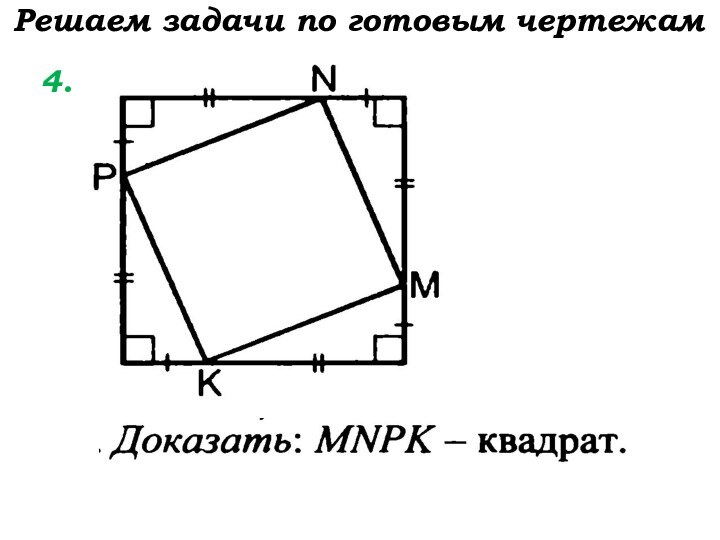
- 10. Решаем задачи по готовым чертежам 4.
- 11. Теорема Пифагора§3,п.5517.12.19
- 12. Ввести теорему Пифагора. Учиться решать задачи на
- 13. Стр.128-129Теорема Пифагора.Читаем формулировку и доказательство теоремы.
- 14. В тетрадь:СВАасb∆ABC – прямоугольныйа и b –
- 15. СВАасb∆ABC – прямоугольныйа и b – катетыс
- 16. В тетрадь:СВАасb∆ABC – прямоугольныйа и b –
- 17. СВАасb∆ABC – прямоугольныйа и b – катетыс
- 18. СВАасb∆ABC – прямоугольныйа и b – катетыс
- 19. СВАасb∆ABC – прямоугольныйа и b – катетыс
- 20. СВАасb∆ABC – прямоугольныйа и b – катетыс
- 21. СВАасb∆ABC – прямоугольныйа и b – катетыс
- 22. СВАасb∆ABC – прямоугольныйа и b – катетыс
- 23. СВАасb∆ABC – прямоугольныйа и b – катетыс
- 24. СВАасb∆ABC – прямоугольныйа и b – катетыс
- 25. СВАасb∆ABC – прямоугольныйа и b – катетыс
- 26. №484 (а,г)а=12, с=13, b - ?Что дано в задаче?Как найти требуемое?
- 27. №484 (а)а=12, с=13, b - ?с² = а²+ b²
- 28. №484 (а)а=12, с=13, b - ?с² = а²+ b²b² = с² – а²
- 29. №484 (а)а=12, с=13, b - ?с² =
- 30. №484 (а)а=12, с=13, b - ?с² =
- 31. №484 (а)а=12, с=13, b - ?с² =
- 32. №484 (а)а=12, с=13, b - ?с² =
- 33. №484 (а)а=12, с=13, b - ?с² =
- 34. №484 (а)а=12, с=13, b - ?с² =
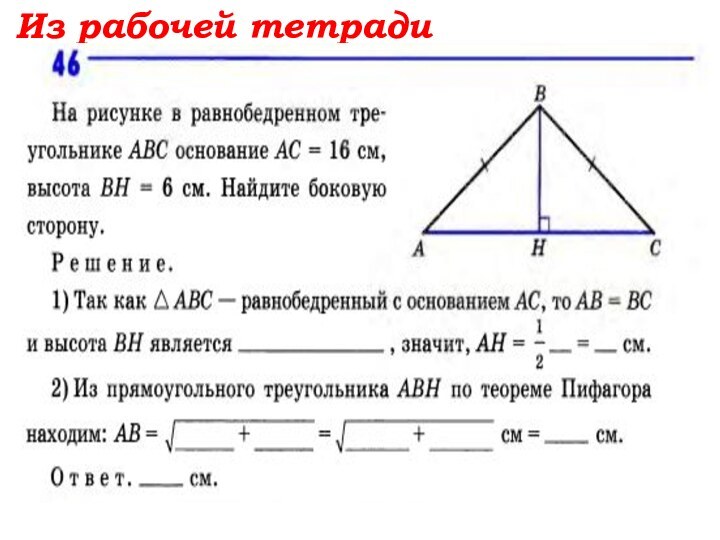
- 35. Из рабочей тетради задачи №45,46Обращаем внимание на форму записи
- 36. Из рабочей тетради
- 37. №484 (г)а= , с= 2b, b - ?
- 38. №484 (г)а= , с= 2b,
- 39. №484 (г)а= , с= 2b,
- 40. №484 (г)а= , с= 2b,
- 41. №484 (г)а= , с= 2b,
- 42. №484 (г)а= , с= 2b,
- 43. №484 (г)а= , с= 2b,
- 44. №484 (г)а= , с= 2b,
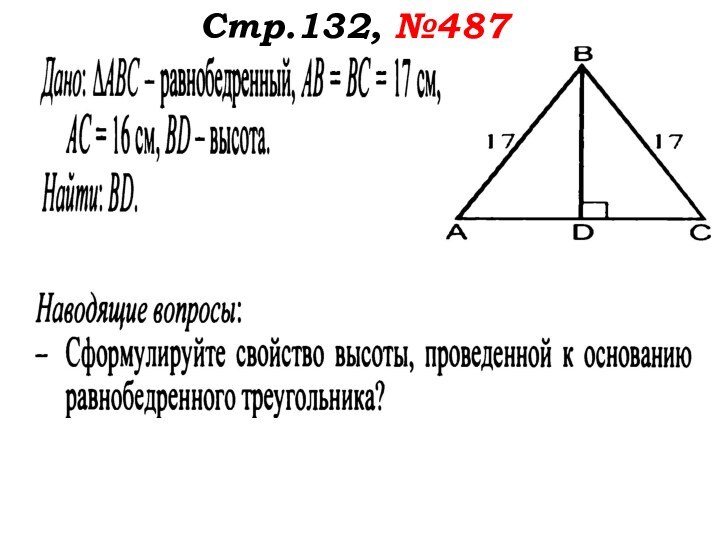
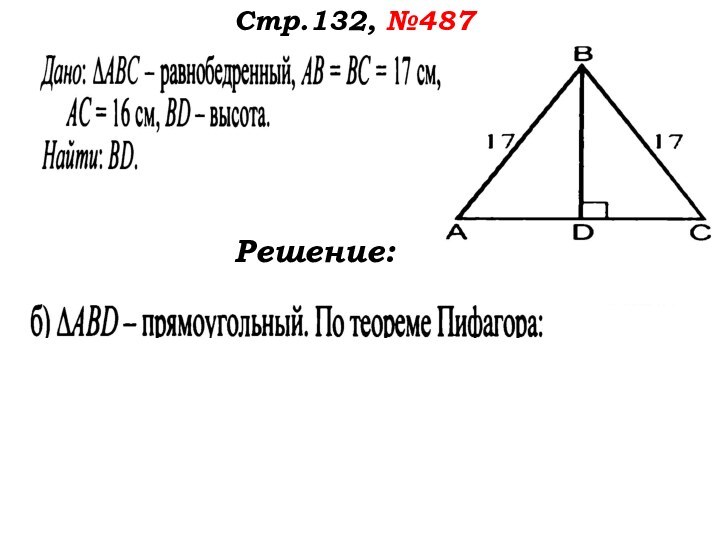
- 45. Стр.132, №487Читаем задачу.Какой треугольник дан?Что нужно найти?
- 46. Стр.132, №487
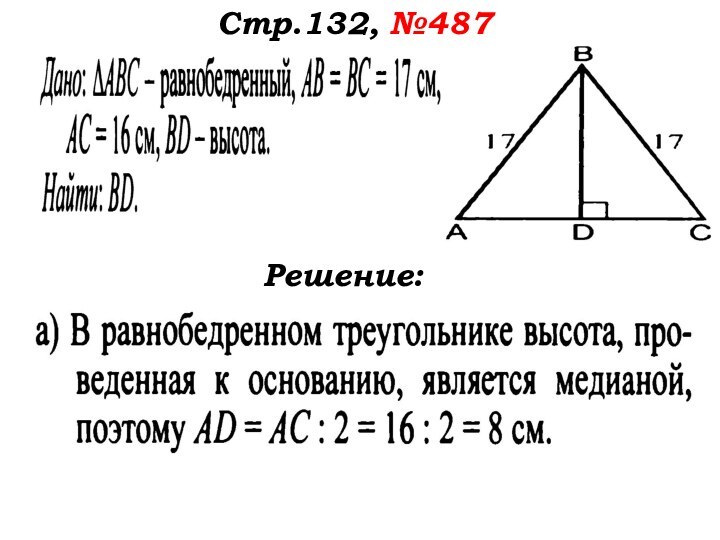
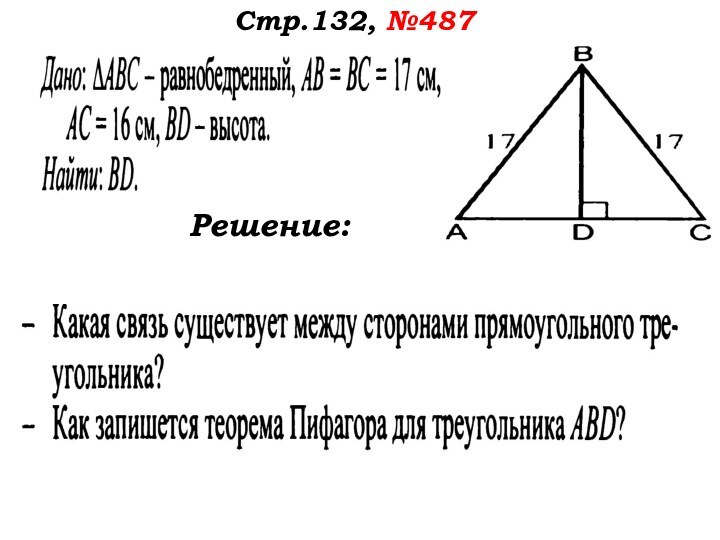
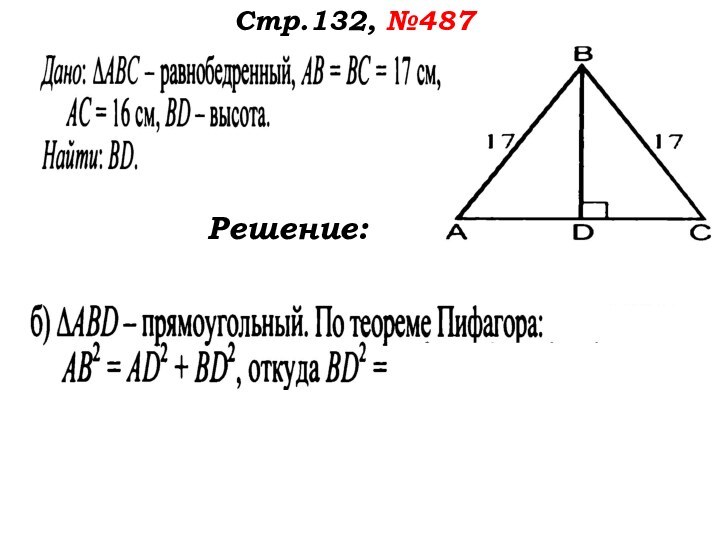
- 47. Стр.132, №487Решение:
- 48. Стр.132, №487Решение:
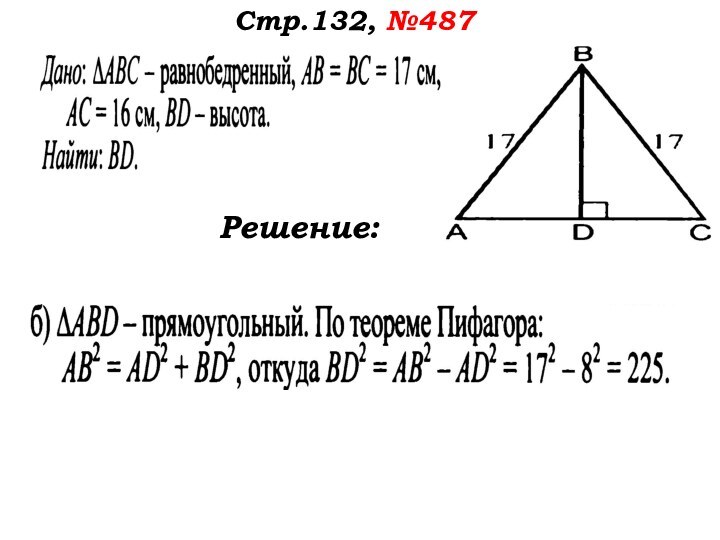
- 49. Стр.132, №487Решение:
- 50. Стр.132, №487Решение:
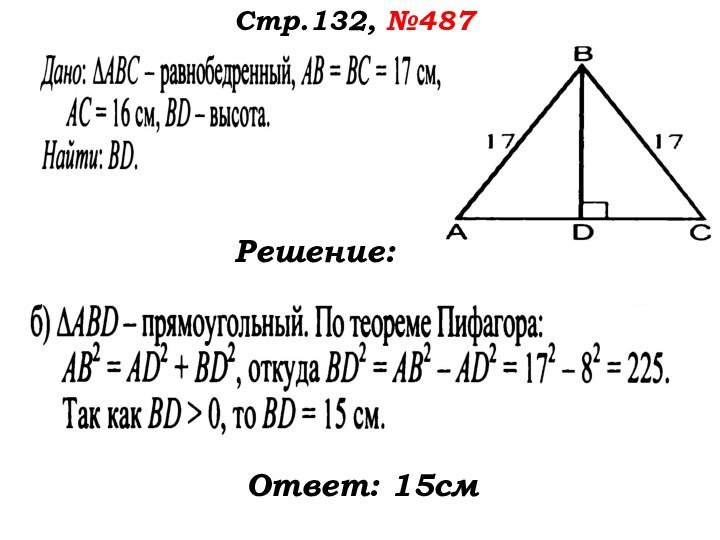
- 51. Стр.132, №487Решение:
- 52. Стр.132, №487Решение:Ответ: 15см
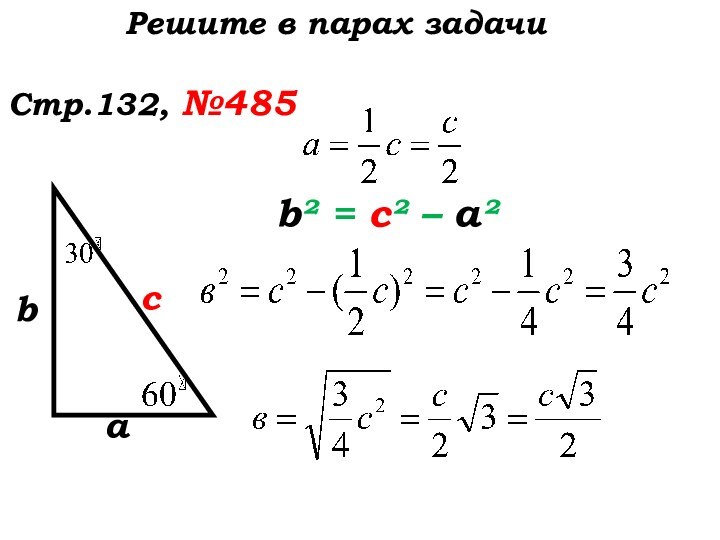
- 53. Решите в парах задачиСтр.132, №485,486(б)Дополнительные задачи
- 54. Решите в парах задачиСтр.132, №485асbb² = с² – а²
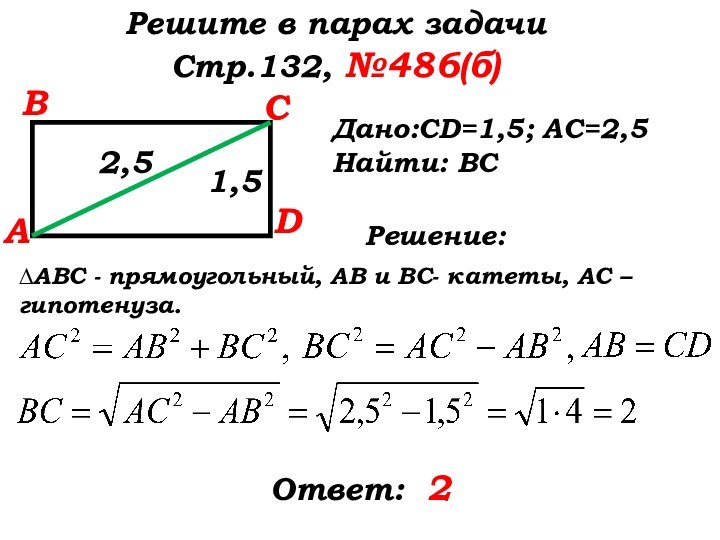
- 55. Решите в парах задачиСтр.132, №486(б)АВСDДано:CD=1,5; AC=2,5Найти: ВСРешение:1,52,5∆АВС - прямоугольный, АВ и ВС- катеты, АС – гипотенуза.
- 56. Решите в парах задачиСтр.132, №486(б)АВСDДано:CD=1,5; AC=2,5Найти: ВСРешение:1,52,5∆АВС - прямоугольный, АВ и ВС- катеты, АС – гипотенуза.
- 57. Решите в парах задачиСтр.132, №486(б)АВСDДано:CD=1,5; AC=2,5Найти: ВСРешение:1,52,5∆АВС
- 59. 13812
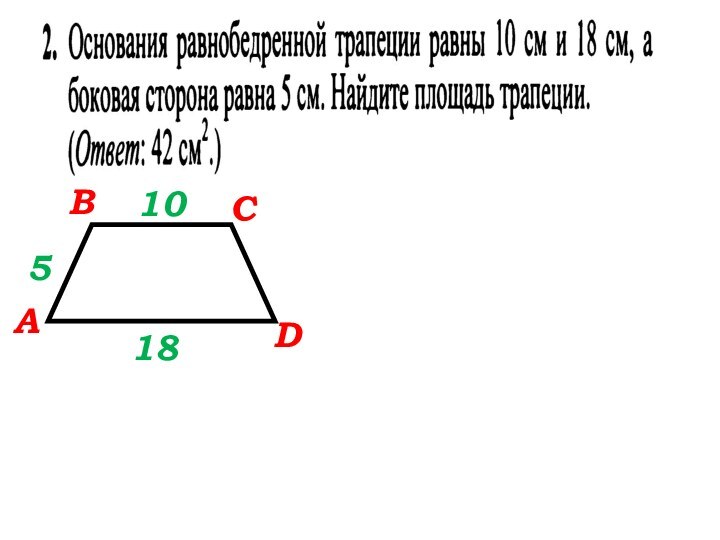
- 60. DВСА10185
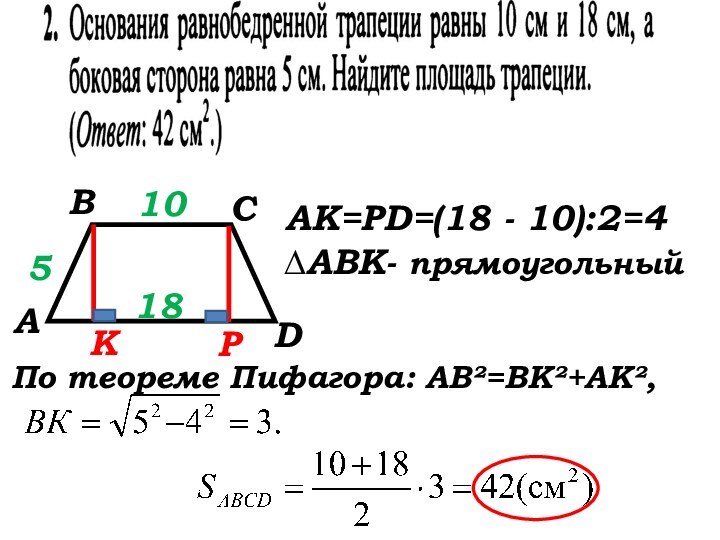
- 61. DВСА10185КРАК=РD=(18 - 10):2=4∆АВК- прямоугольныйПо теореме Пифагора: АВ²=ВК²+АК²,
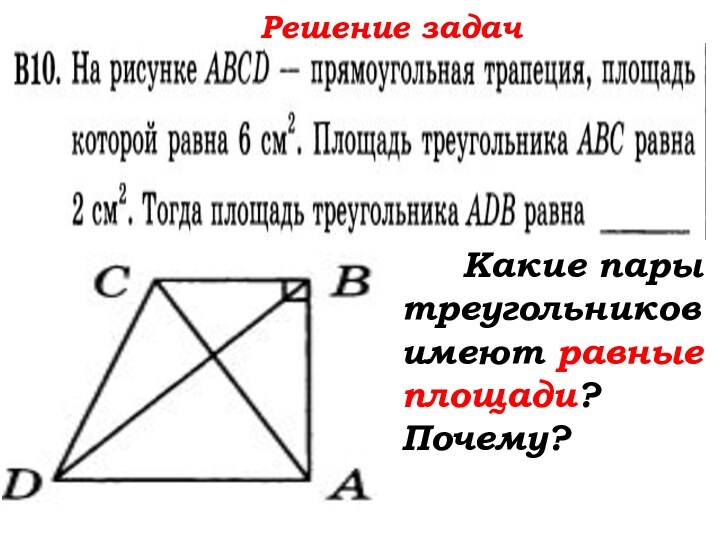
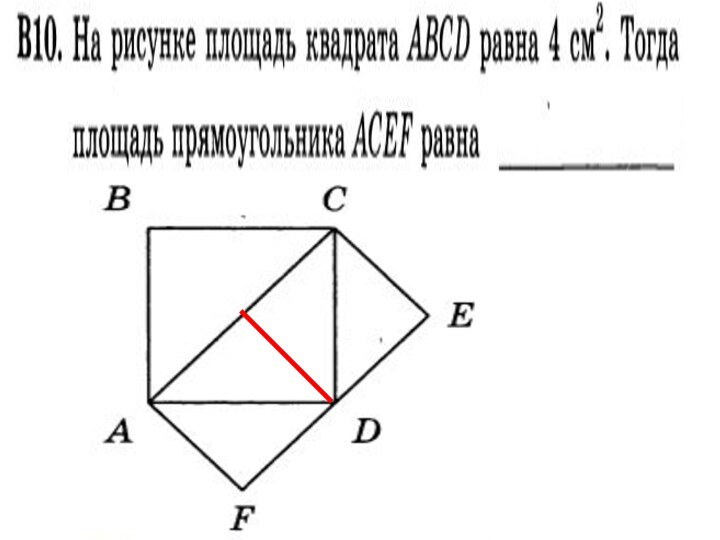
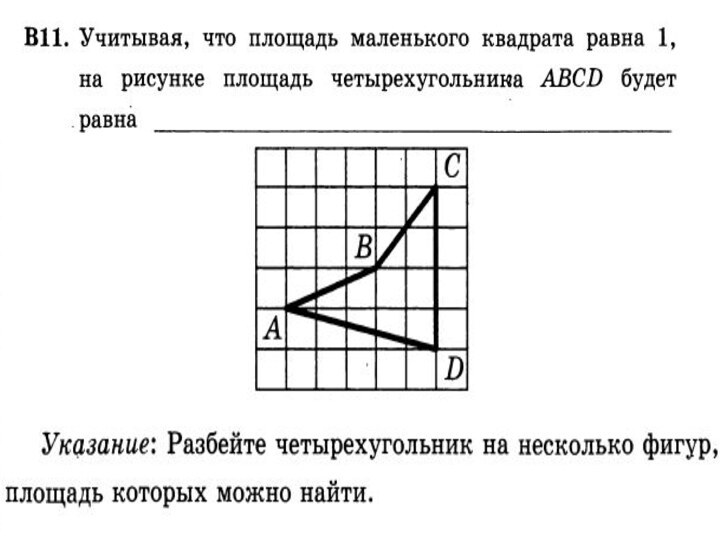
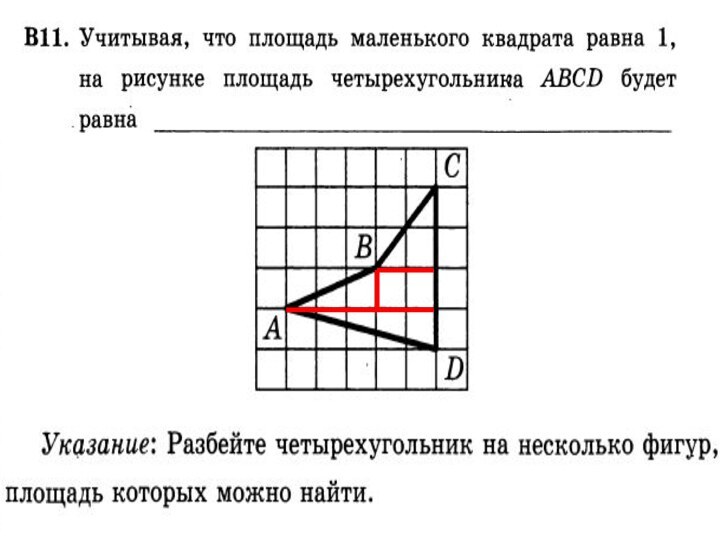
- 62. Решение задач Какие пары треугольников имеют равные площади?Почему?
- 68. Подводим
- 69. Критерии
- 70. Назовите
- 71. Скачать презентацию
- 72. Похожие презентации



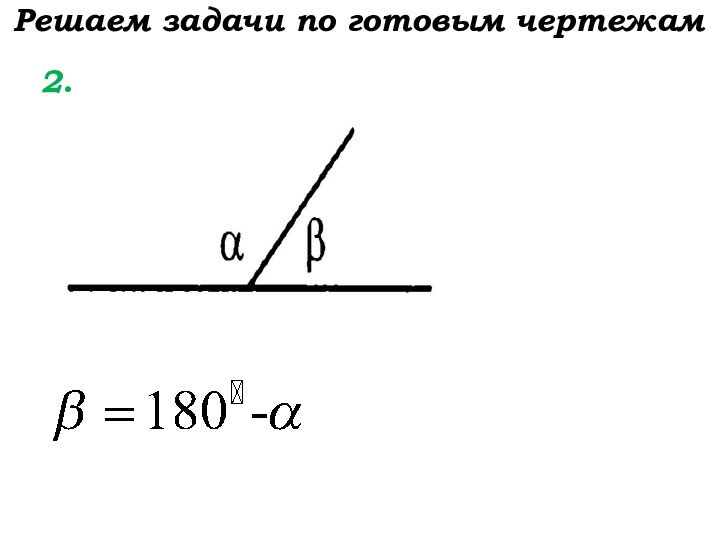






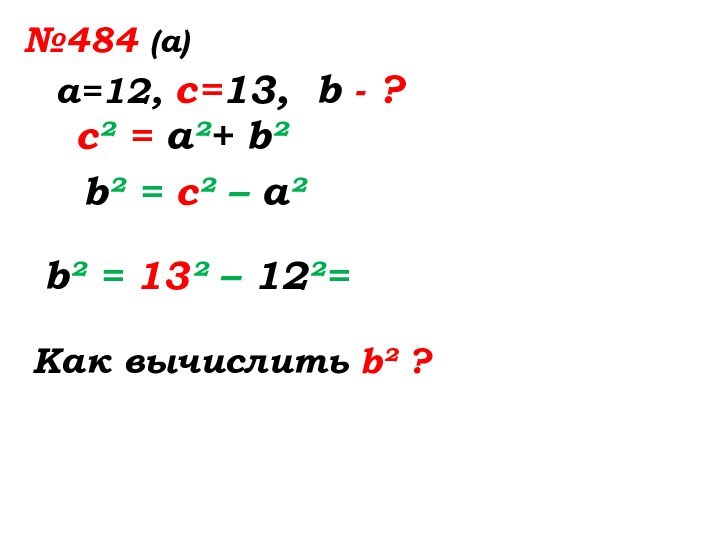
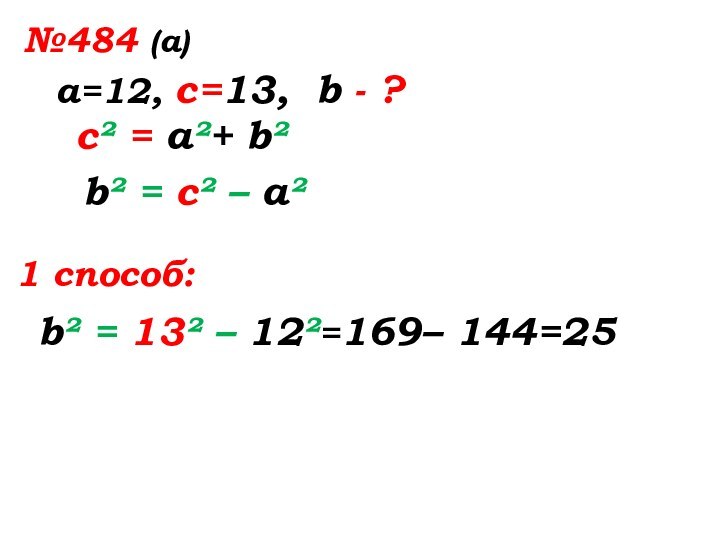

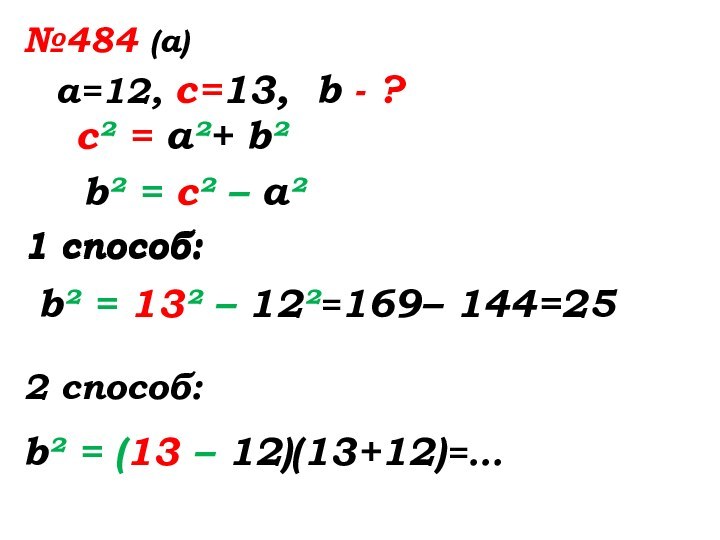

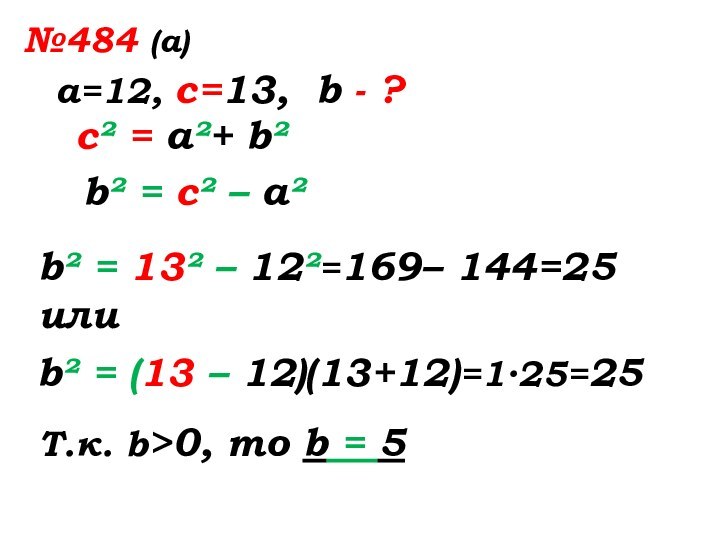

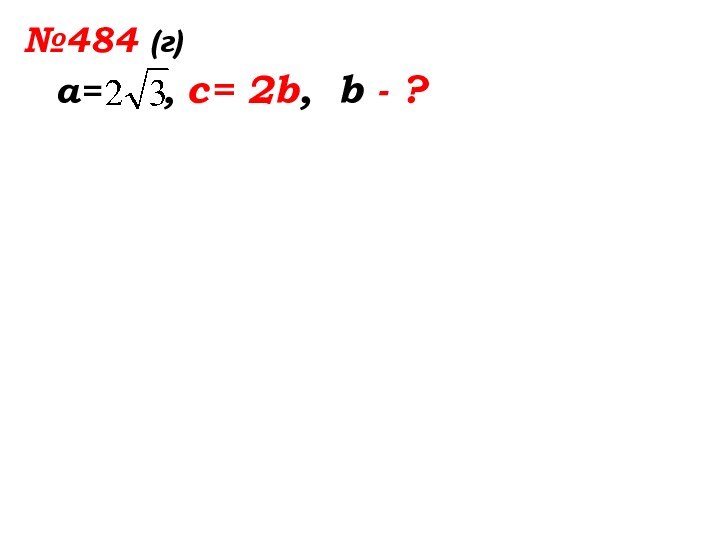
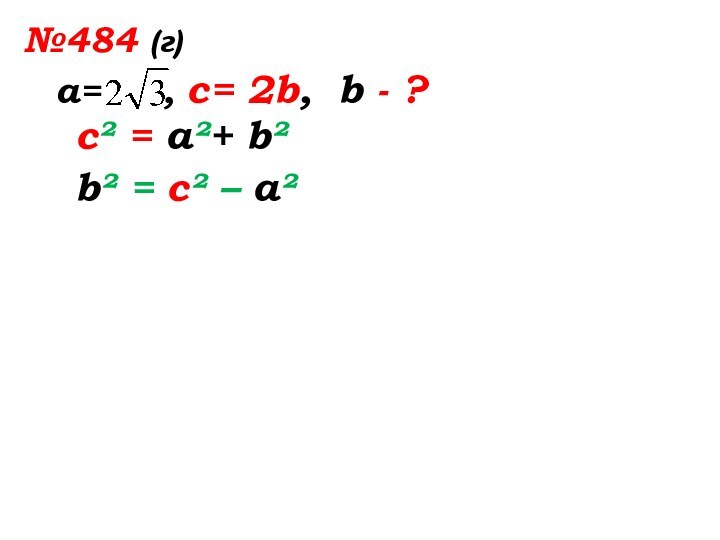
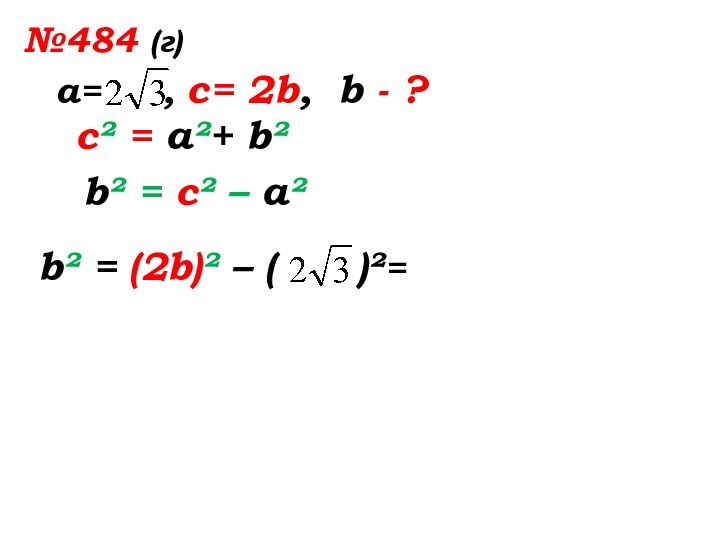
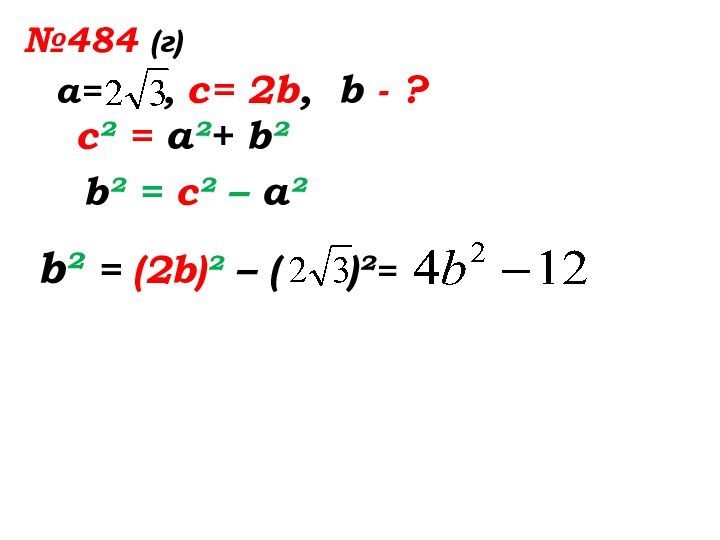
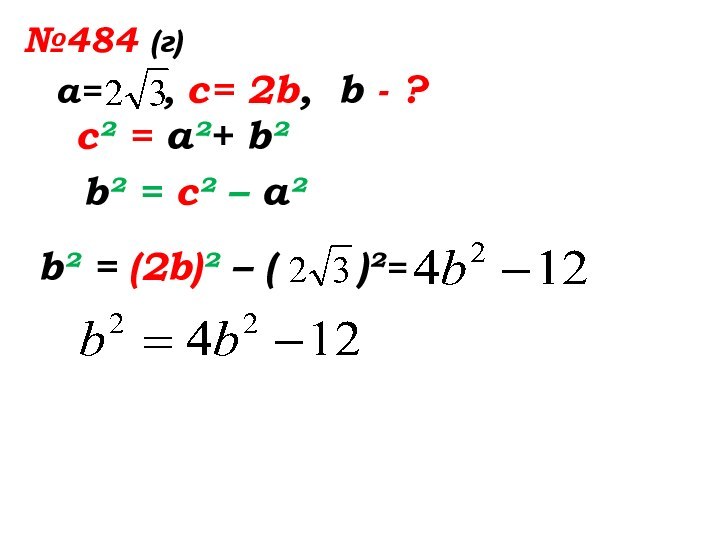
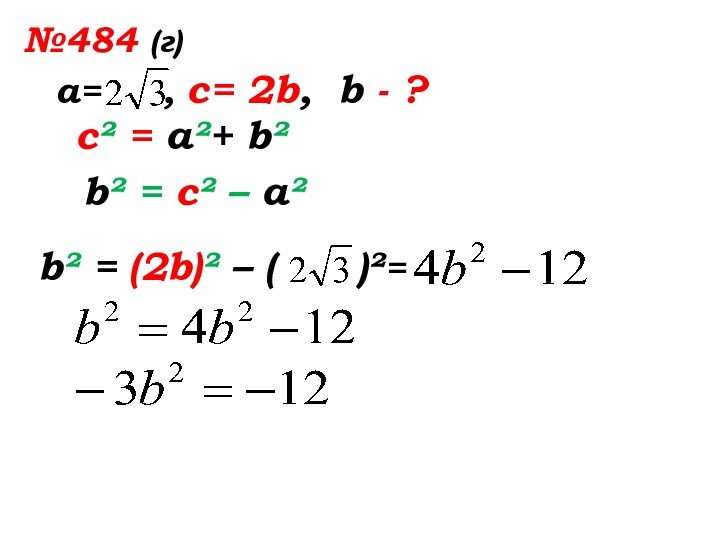
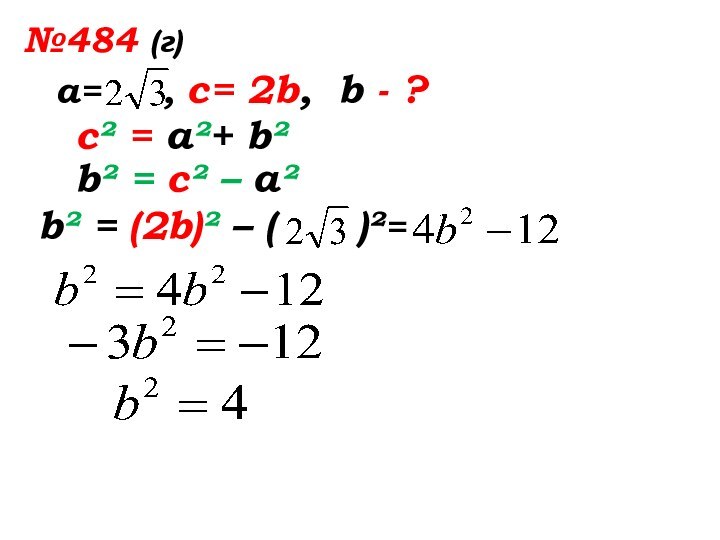
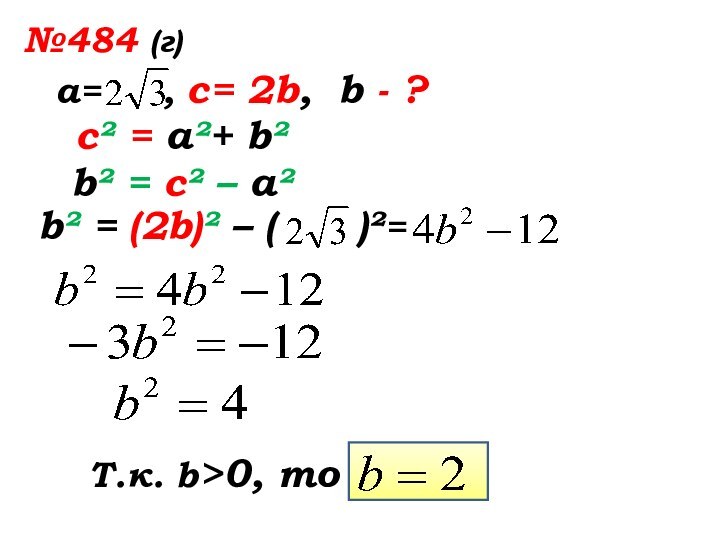






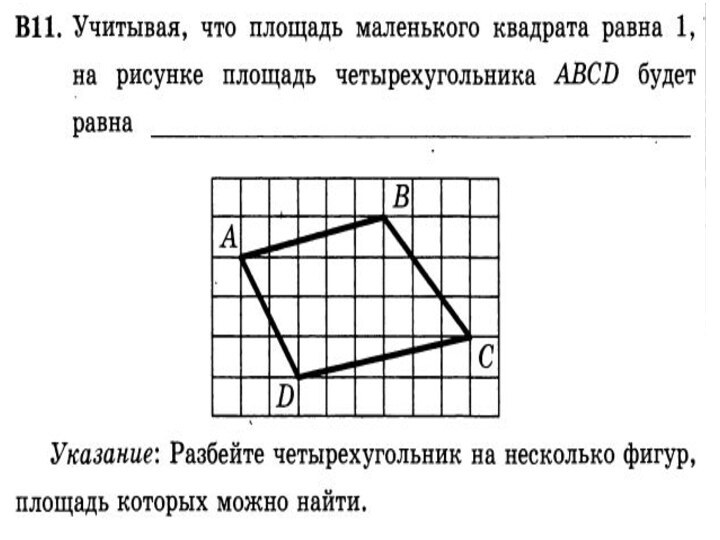
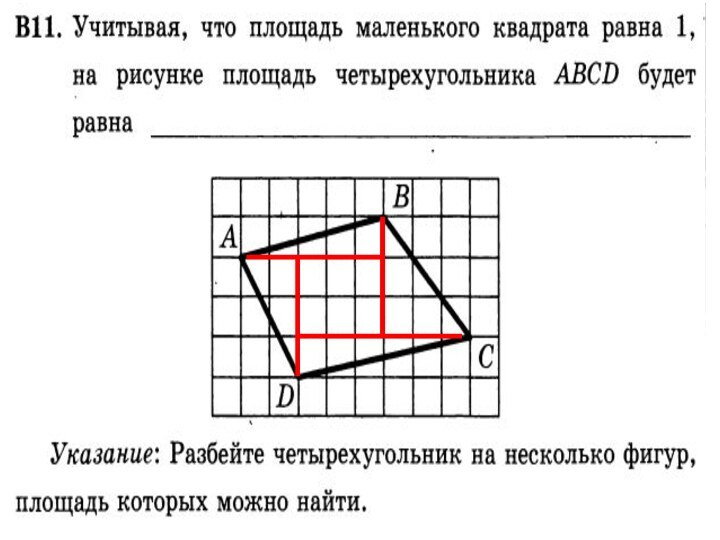




Слайд 3
Успешного усвоения материала
Интересные мысли
и высказывания
Чтобы дойти до цели,
надо прежде всего
идти. О.Бальзак
Слайд 12
Ввести теорему Пифагора.
Учиться решать задачи на применение
теоремы Пифагора.
Формировать правильную математическую речь, совершенствовать навыки решения задач.
Цели
урока:
Слайд 14
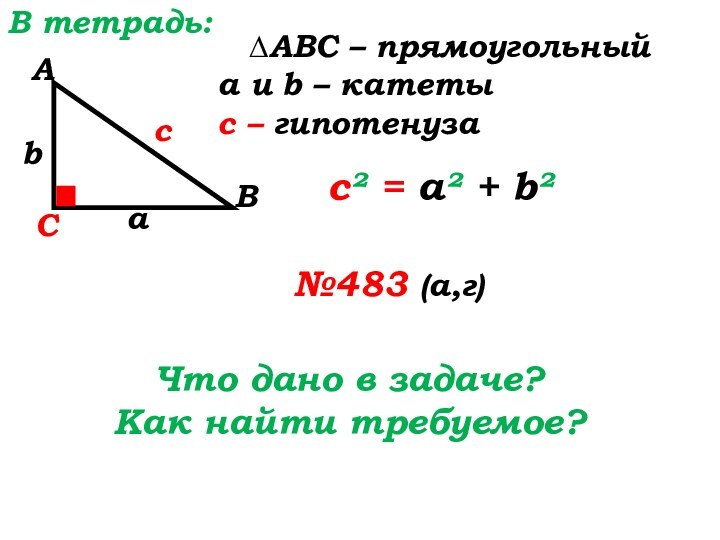
В тетрадь:
С
В
А
а
с
b
∆ABC – прямоугольный
а и b – катеты
с
– гипотенуза
с² = а² + b²
№483 (а,г)
Что дано в
задаче?Как найти требуемое?
Слайд 16
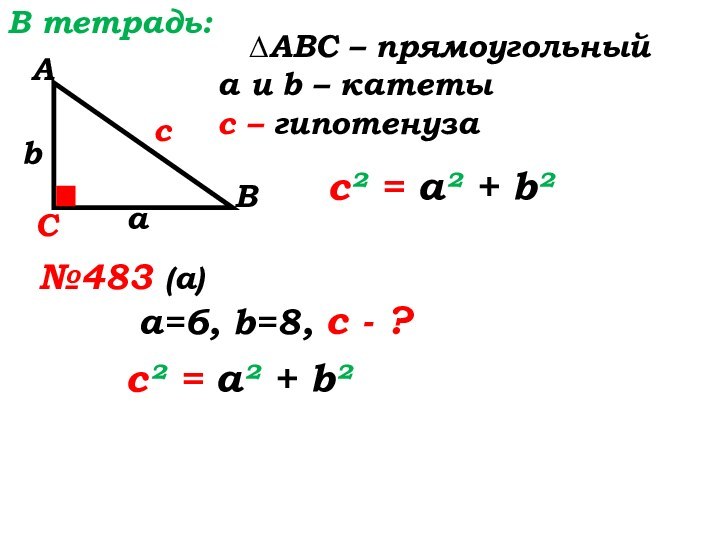
В тетрадь:
С
В
А
а
с
b
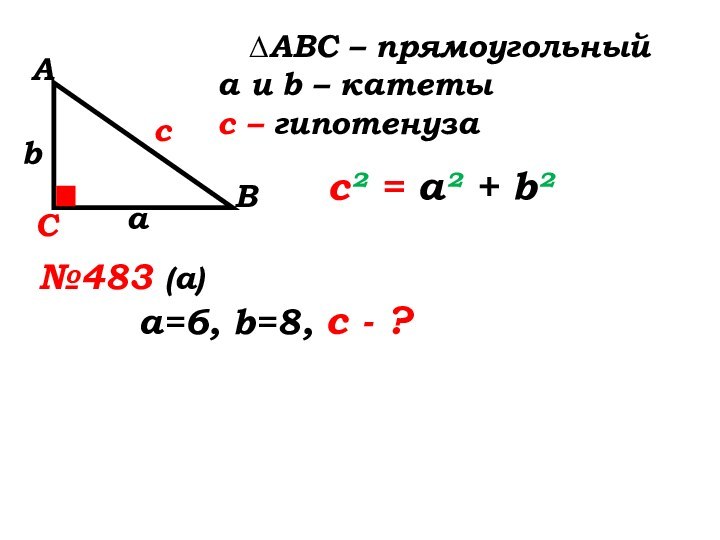
∆ABC – прямоугольный
а и b – катеты
с
– гипотенуза
с² = а² + b²
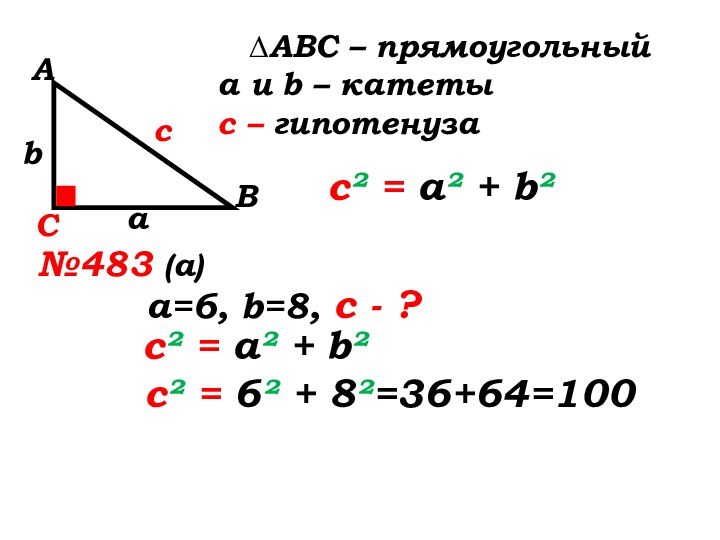
№483 (а)
а=6, b=8, с
- ?с² = а² + b²
Слайд 17
С
В
А
а
с
b
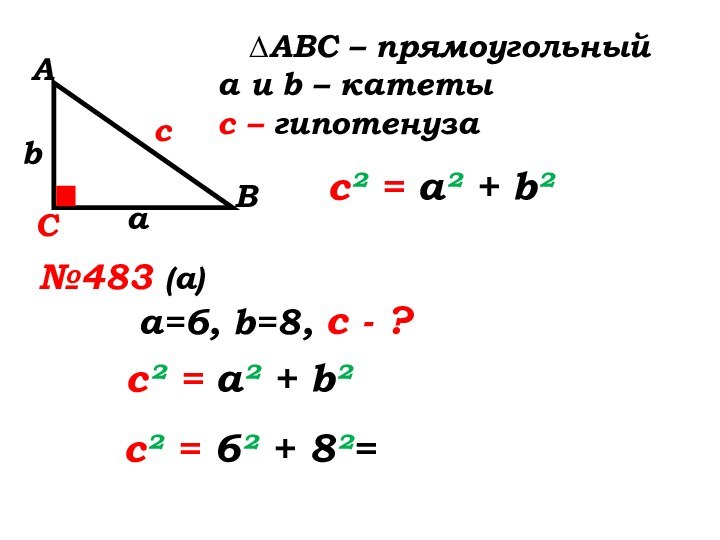
∆ABC – прямоугольный
а и b – катеты
с –
гипотенуза
с² = а² + b²
№483 (а)
а=6, b=8, с -
?с² = а² + b²
с² = 6² + 8²=
Слайд 18
С
В
А
а
с
b
∆ABC – прямоугольный
а и b – катеты
с –
гипотенуза
с² = а² + b²
№483 (а)
а=6, b=8, с -
?с² = а² + b²
с² = 6² + 8²=36+64=100
Слайд 19
С
В
А
а
с
b
∆ABC – прямоугольный
а и b – катеты
с –
гипотенуза
с² = а² + b²
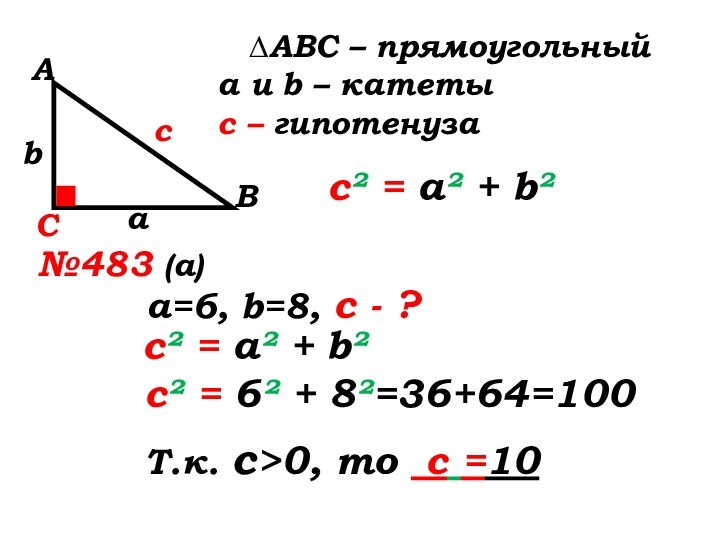
№483 (а)
а=6, b=8, с -
?с² = а² + b²
с² = 6² + 8²=36+64=100
Т.к. с>0, то с =10
Слайд 21
С
В
А
а
с
b
∆ABC – прямоугольный
а и b – катеты
с –
гипотенуза
с² = а² + b²
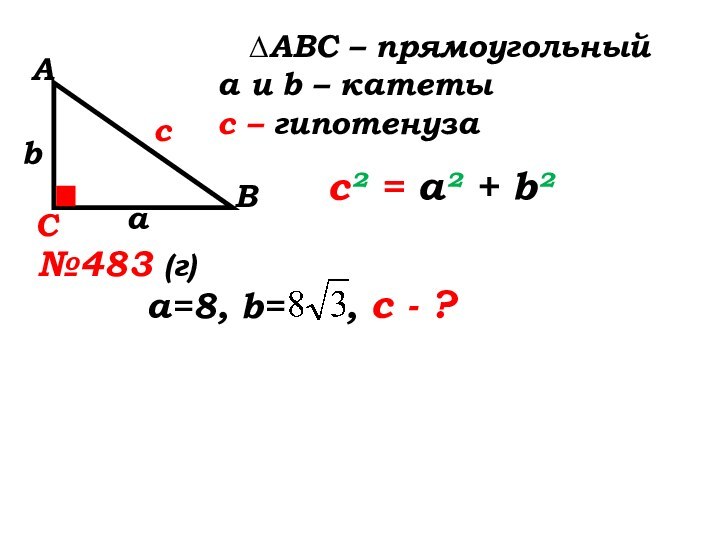
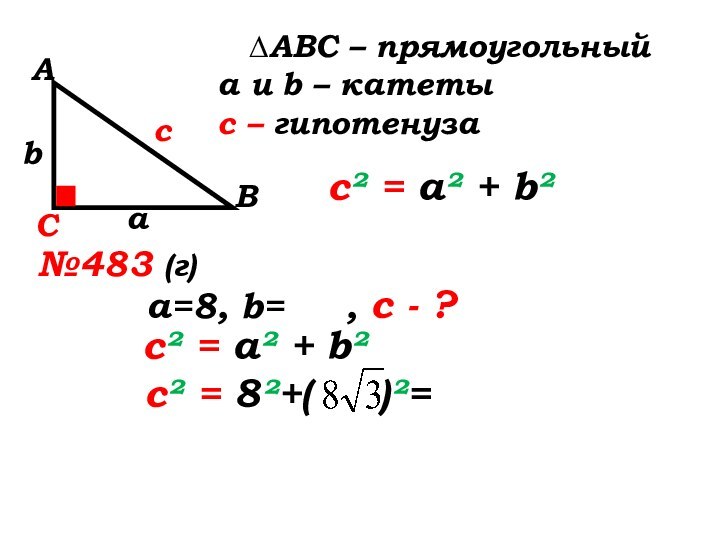
№483 (г)
а=8, b=
, с - ?с² = а² + b²
Слайд 22
С
В
А
а
с
b
∆ABC – прямоугольный
а и b – катеты
с –
гипотенуза
с² = а² + b²
№483 (г)
а=8, b=
, с - ?с² = а² + b²
с² = 8²+( )²=
Слайд 23
С
В
А
а
с
b
∆ABC – прямоугольный
а и b – катеты
с –
гипотенуза
с² = а² + b²
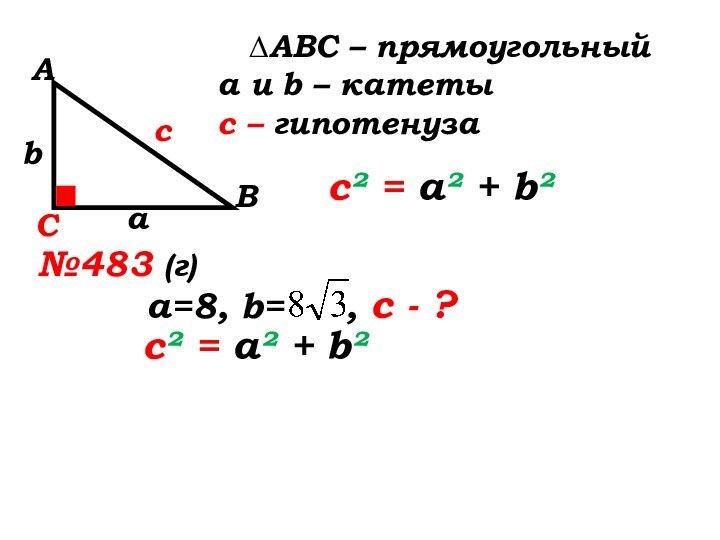
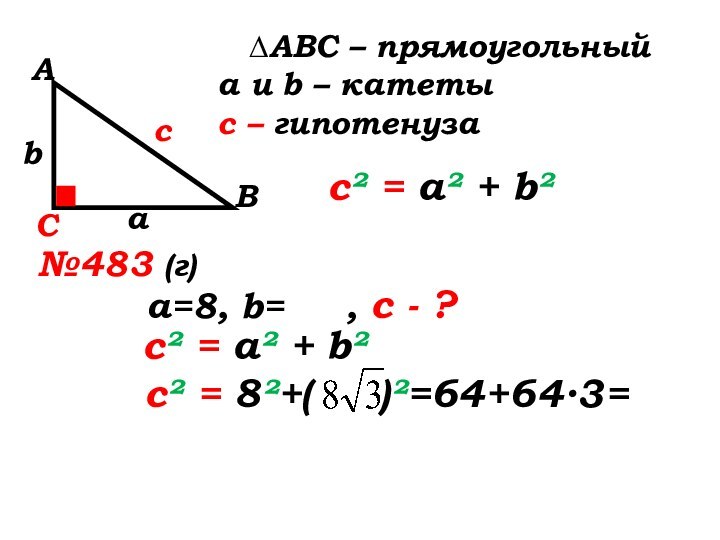
№483 (г)
а=8, b=
, с - ?с² = а² + b²
с² = 8²+( )²=64+64∙3=
Слайд 24
С
В
А
а
с
b
∆ABC – прямоугольный
а и b – катеты
с –
гипотенуза
с² = а² + b²
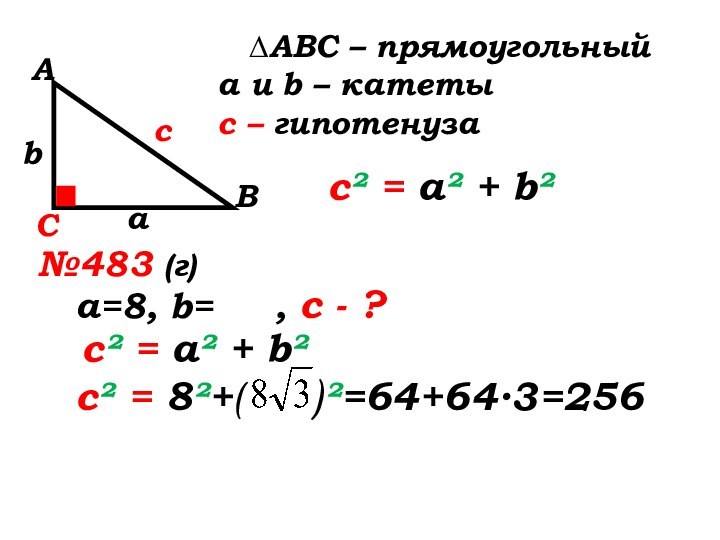
№483 (г)
а=8, b=
, с - ?с² = а² + b²
с² = 8²+( )²=64+64∙3=256
Слайд 25
С
В
А
а
с
b
∆ABC – прямоугольный
а и b – катеты
с –
гипотенуза
с² = а² + b²
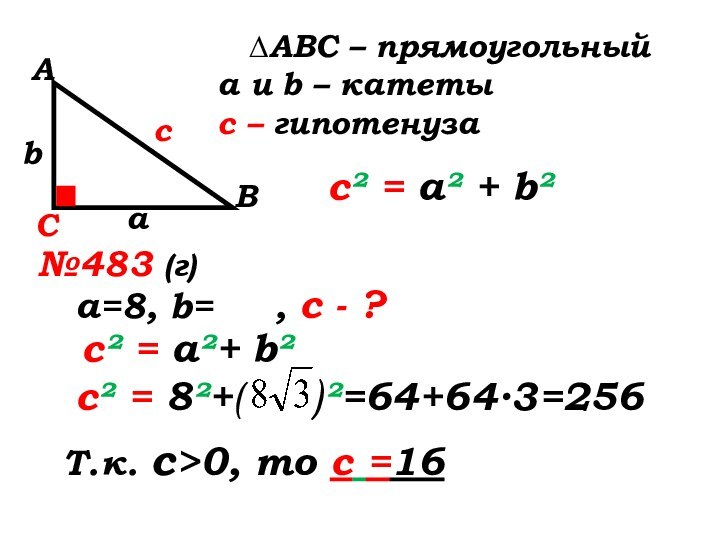
№483 (г)
а=8, b=
, с - ?с² = а²+ b²
с² = 8²+( )²=64+64∙3=256
Т.к. с>0, то с =16
Слайд 31
№484 (а)
а=12, с=13, b - ?
с² = а²+
b²
b² = с² – а²
b² = 13² – 12²=169–
144=251 способ:
1 способ:
2 способ:
Слайд 32
№484 (а)
а=12, с=13, b - ?
с² = а²+
b²
b² = с² – а²
b² = 13² – 12²=169–
144=251 способ:
1 способ:
2 способ:
b² = (13 – 12)(13+12)=…
Слайд 33
№484 (а)
а=12, с=13, b - ?
с² = а²+
b²
b² = с² – а²
b² = 13² – 12²=169–
144=251 способ:
1 способ:
2 способ:
b² = (13 – 12)(13+12)=1∙25=25
Слайд 34
№484 (а)
а=12, с=13, b - ?
с² = а²+
b²
b² = с² – а²
b² = 13² – 12²=169–
144=25или
Т.к. b>0, то b = 5
b² = (13 – 12)(13+12)=1∙25=25
Слайд 55
Решите в парах задачи
Стр.132, №486(б)
А
В
С
D
Дано:CD=1,5; AC=2,5
Найти: ВС
Решение:
1,5
2,5
∆АВС -
прямоугольный, АВ и ВС- катеты, АС – гипотенуза.
Слайд 56
Решите в парах задачи
Стр.132, №486(б)
А
В
С
D
Дано:CD=1,5; AC=2,5
Найти: ВС
Решение:
1,5
2,5
∆АВС -
прямоугольный, АВ и ВС- катеты, АС – гипотенуза.
Слайд 57
Решите в парах задачи
Стр.132, №486(б)
А
В
С
D
Дано:CD=1,5; AC=2,5
Найти: ВС
Решение:
1,5
2,5
∆АВС -
прямоугольный, АВ и ВС- катеты, АС – гипотенуза.
Ответ: 2
Слайд 68
Подводим
итоги:
Как называются стороны в прямоугольном треугольнике?
Какой зависимостью связаны стороны в прямоугольном треугольнике?
Слайд 69
Критерии
оценки за урок:
1. Комментировали ДЗ
2. Активно участвовали в решении
устных задач.3. Привели решение задач, решаемых письменно
Поставьте себе оценку за урок