- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Перпендикулярность прямой и плоскости
Содержание
- 2. Прямая называется перпендикулярной к плоскости, если она
- 5. Доказательство леммы
- 6. Доказательство признака перпендикулярности прямой и плоскостиПусть a — прямая,
- 7. Задача №1Прямая РQ параллельна плоскости α . Через точки Р и Q проведены
- 8. Задача№2Через точки P и Q прямой PQ проведены прямые, перпендикулярные плоскости α и
- 9. Задача№3 Номер 127В треугольнике ABC
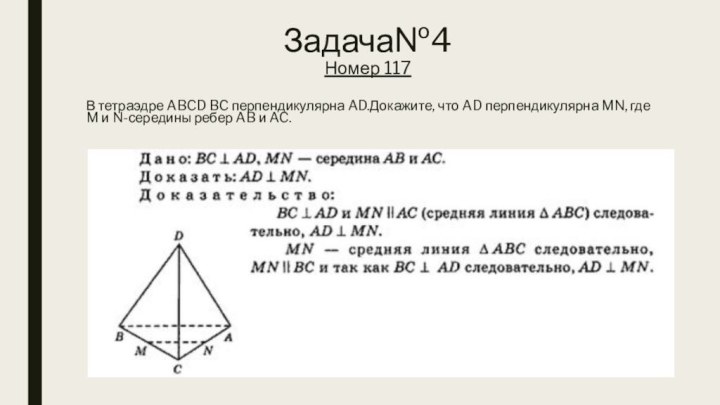
- 10. Задача№4 Номер 117В тетраэдре ABCD BC перпендикулярна
- 11. Признак перпендикулярности прямой и плоскости
- 12. Скачать презентацию
- 13. Похожие презентации
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскостиОпределениеПерпендикулярность прямой и плоскости обозначается как a⊥α.











Слайд 2 Прямая называется перпендикулярной к плоскости, если она перпендикулярна
к любой прямой, лежащей в этой плоскости
плоскости обозначается как a⊥α.Слайд 3
Теоремы
1. ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ.
Если
прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна плоскости. (рис. 1)2. 1-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ.
Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой. (Рис. 2)
3. 2-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ.
Если две прямые перпендикулярные к плоскости, то они параллельны. (рис. 2)
4. 3-е СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ.
Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна. (рис. 3)
Рис. 1
Рис. 2
Рис.3
Слайд 4
Лемма
Если одна из двух параллельных
прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
Слайд 6
Доказательство признака перпендикулярности прямой и плоскости
Пусть a — прямая, перпендикулярная
прямым b и c в плоскости. Проведём прямую a через точку A пересечения прямых b и c. Докажем, что прямая a перпендикулярна
плоскости, то есть каждой прямой в этой плоскости.1. Проведём произвольную прямую x через точку A в плоскости и покажем, что она перпендикулярна прямой a. Проведём в плоскости произвольную прямую, не проходящую через точку A и пересекающую прямые b, c и x. Пусть точками пересечения будут B, C и X.
2. Отложим на прямой a от точки A в разные стороны равные отрезки AM и AN.
3. Треугольник MCN равнобедренный, так как отрезок AC является высотой по условию теоремы и медианой по построению (AM=AN). По той же причине треугольник MBN тоже равнобедренный.
4. Следовательно, треугольники MBC и NBC равны по трём сторонам.
5. Из равенства треугольников MBC и NBC следует равенство углов MBX и NBX и, следовательно, равенство треугольников MBX и NBX по двум сторонам и углу между ними.
6. Из равенства сторон MX и NX этих треугольников заключаем, что треугольник MXN равнобедренный. Поэтому его медиана XA является также высотой. А это и значит, что прямая x перпендикулярна a. По определению прямая a перпендикулярна плоскости.
Слайд 7
Задача №1
Прямая РQ параллельна плоскости α . Через точки Р и Q проведены прямые,
перпендикулярные к плоскости α, которые пересекают эту плоскость соответственно
в точках Р1 и Q1. Докажите, что PQ = P1Q1.