- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Призма (10 класс)
Содержание
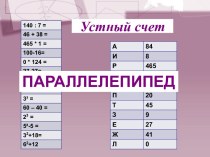
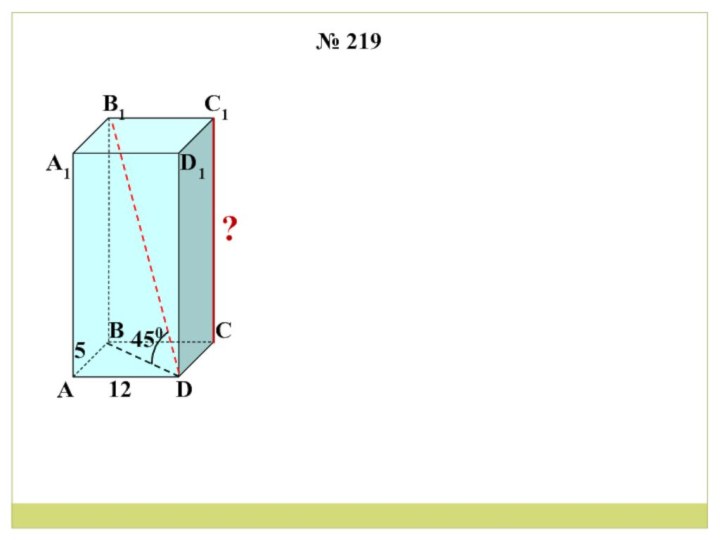
- 2. Дома: п. 30 с. 60-61,с. 67 № 218 а), № 229 а)Призма
- 3. abРассмотрим два равных многоугольника А1А2…Аn и B1B2…Bn
- 4. abА1А2АnB1Bn B2Равные многоугольники А1А2…Аn и B1B2…Bn называются
- 5. Треугольная призмаЧетырёхугольная призмаШестиугольная призмаПризма называется прямой, если боковые рёбра призмы перпендикулярны к основаниям.
- 6. Призма называется наклонной, если боковые рёбра призмы
- 7. Призма называется прямой, если боковые рёбра призмы
- 8. Теорема Площадь боковой поверхности прямой призмы равна
- 9. № 229 б) с. 68В правильной n-угольной
- 10. ЕГЭ профиль задание 8 Сторона основания правильной
- 11. ЕГЭ профиль задание 8 Площадь боковой поверхности
- 12. ЕГЭ база задание 16 Два ребра прямоугольного
- 13. ЕГЭ база задание 13 Ящик имеет форму
- 14. Скачать презентацию
- 15. Похожие презентации










Слайд 3
a
b
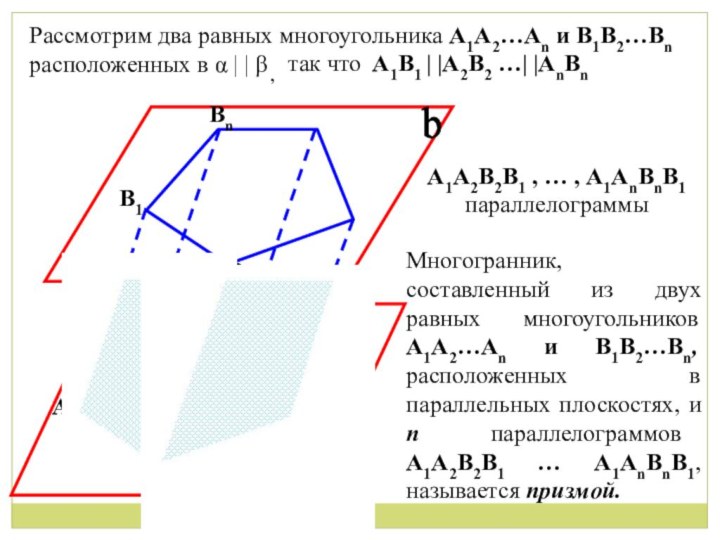
Рассмотрим два равных многоугольника А1А2…Аn и B1B2…Bn
расположенных
в ,
А1
А2
Аn
B1
Bn
B2
так что
А1B1
А2B2 … АnBnА1А2B2B1 , … , А1АnBnB1 параллелограммы
Многогранник, составленный из двух равных многоугольников А1А2…Аn и В1B2…Bn, расположенных в параллельных плоскостях, и п параллелограммов А1А2B2B1 … А1АnBnB1, называется призмой.
Слайд 4
a
b
А1
А2
Аn
B1
Bn
B2
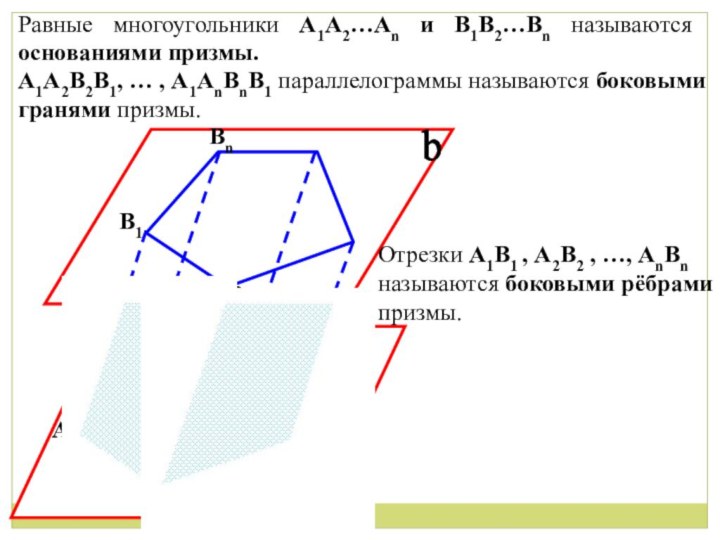
Равные многоугольники А1А2…Аn и B1B2…Bn называются основаниями
призмы.
А1А2B2B1, … , А1АnBnB1 параллелограммы называются боковыми гранями призмы.
Отрезки А1B1 , А2B2 , …, АnBn называются боковыми рёбрами призмы.
Слайд 5
Треугольная призма
Четырёхугольная призма
Шестиугольная призма
Призма называется прямой, если боковые
рёбра призмы перпендикулярны к основаниям.
Слайд 6 Призма называется наклонной, если боковые рёбра призмы неперпендикулярны
к основаниям.
Перпендикуляр, проведённый из какой-нибудь точки одного основания к
плоскости другого основания, называется высотой призмы.Н
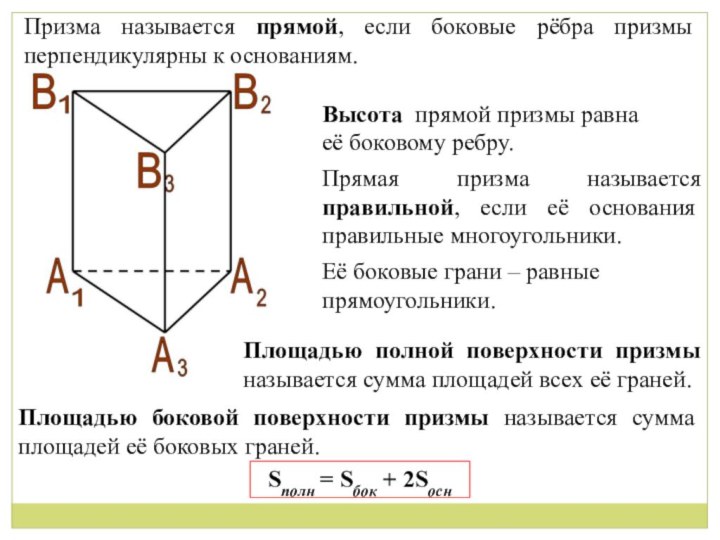
Слайд 7 Призма называется прямой, если боковые рёбра призмы перпендикулярны
к основаниям.
Высота прямой призмы равна
её боковому ребру.
Прямая призма
называется правильной, если её основания правильные многоугольники.Её боковые грани – равные
прямоугольники.
Площадью полной поверхности призмы называется сумма площадей всех её граней.
Площадью боковой поверхности призмы называется сумма площадей её боковых граней.
Sполн = Sбок + 2Sосн
Слайд 8
Теорема
Площадь боковой поверхности прямой призмы равна произведению
периметра основания на высоту призмы.
Площадью боковой поверхности призмы называется
сумма площадей её боковых граней.Sбок= Росн h
Sбок= S1 + S2 + …+ Sn
Sбок= А1А2 h + А2А3 h +…+ А1Аn h
Sбок= (А1А2 + А2А3 +…+ А1Аn) h
Sбок= Росн h
А1
А2
Аn
А3
Слайд 9
№ 229 б) с. 68
В правильной n-угольной призме
сторона основания равна а и высота равна h. Вычислите
площади боковой и полной поверхности призмы, если: б) n = 4, а = 12 дм, h = 8 дм.Sполн = Sбок + 2Sосн
Sбок= Росн h