- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии Применение теоремы Пифагора при решении задач.
Содержание
- 2. «Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора». Иоганн Кеплер
- 3. Закончите предложение:Прямоугольным треугольником называется треугольник, у которого один из углов равен ____90°
- 4. Стороны треугольника, образующие прямой угол, называются _________ катетами
- 5. Сторона треугольника, лежащая против прямого угла, называется____________ гипотенузой
- 6. В прямоугольном треугольнике квадрат гипотенузы равен____________сумме квадратов катетов
- 7. Сформулированное выше предложение носит название____________Теорема Пифагораc² = a² + b²
- 8. Если в треугольнике квадрат одной стороны равен
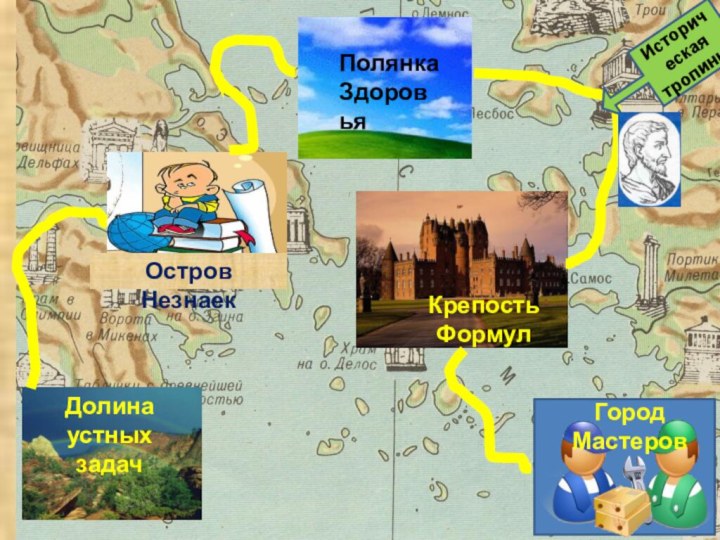
- 10. Долина устных задачОстров НезнаекПолянка ЗдоровьяКрепость ФормулИсторическая тропинка
- 11. Долина устных задач
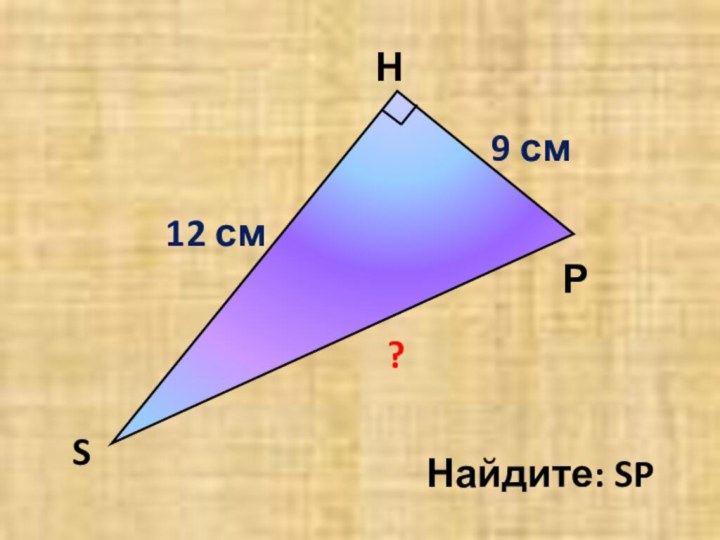
- 12. НS Р12 см9 см 15 см ?Найдите: SP
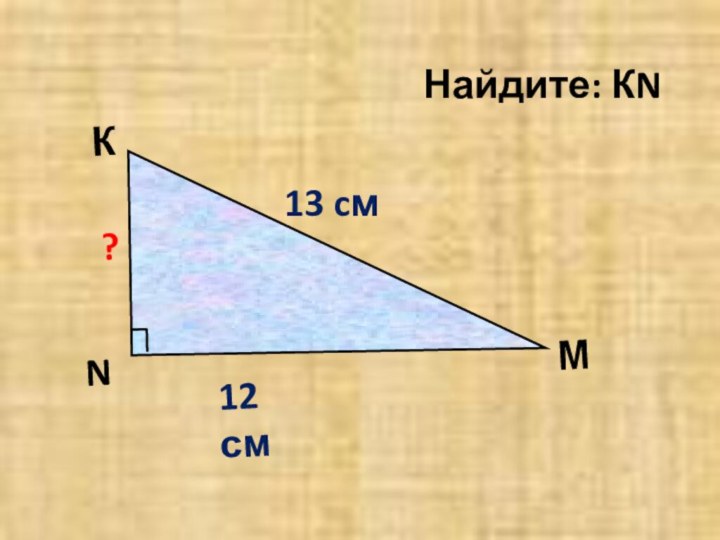
- 13. К?12 см13 cмN МНайдите: КN 5 cм
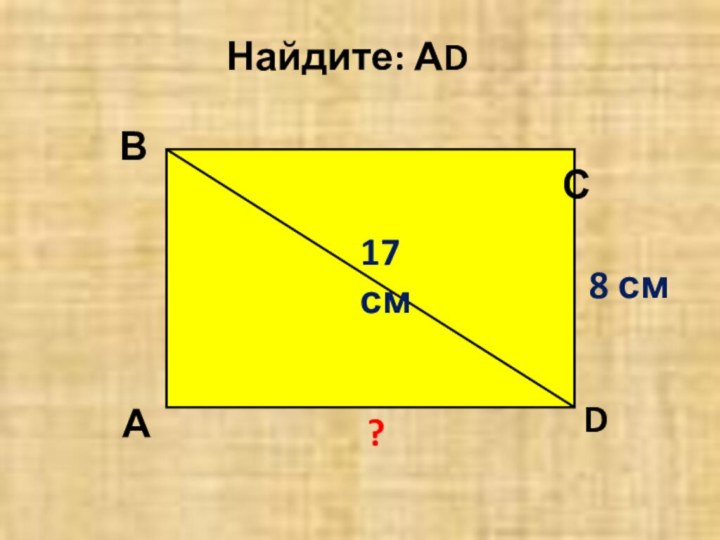
- 14. В? 8 см17 смА D СНайдите: АD 15 cм
- 15. Остров Незнаек
- 16. Задача индийского математика XII века Бхаскары"На берегу
- 17. Из одной точки на земле отправились в
- 18. 8 км6 км? км
- 19. Решаем по учебнику задачу № 494 ( стр. 133)
- 20. Физминутка
- 21. (580 - 500 г. до н.э.)Пифагор
- 22. Дабы познать науки, Пифагор много путешествовал, в
- 23. Пифагорейцы занимались математикой, философией, естественными науками. Ими
- 24. Пентаграмма – это звездчатый пятиугольник, который образован диагоналями правильного пятиугольника.
- 25. Вид пятиконечной звезды имеют цветы, морские звезды и многие другие создания природы.
- 26. Доказательство теоремы Пифагора учащиеся средних
- 27. «Ослиный мост»
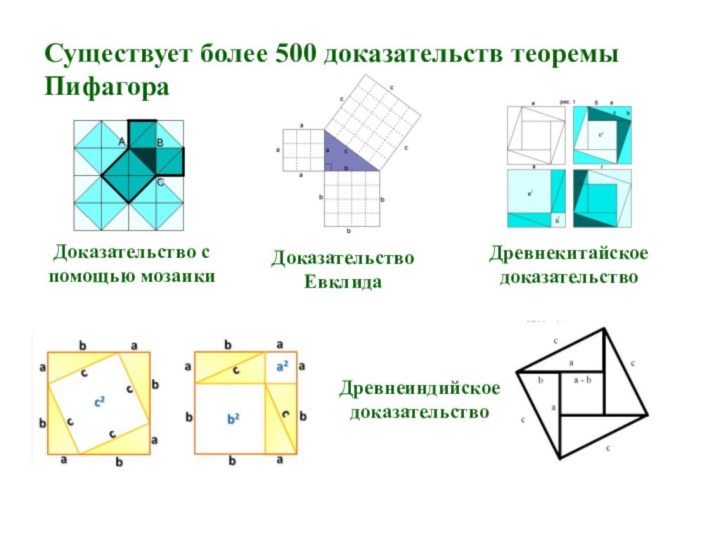
- 28. Существует более 500 доказательств теоремы ПифагораДоказательство с помощью мозаикиДревнекитайское доказательствоДоказательствоЕвклидаДревнеиндийскоедоказательство
- 29. «Штурмуем»Крепость Формул
- 30. Проверь друга!I вариантII вариант
- 31. Ещё землемеры Древнего Египта для построения прямого угла использовали веревку, разделенную узлами на 12 равных частей
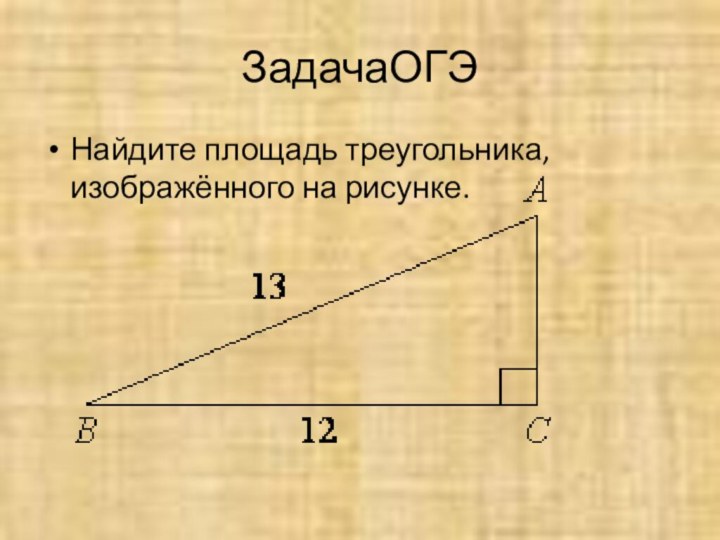
- 32. ЗадачаОГЭНайдите площадь треугольника, изображённого на рисунке.
- 33. Правила написания синквейна: -первая строка – одно
- 34. Теорема Пифагора – это одна из самых
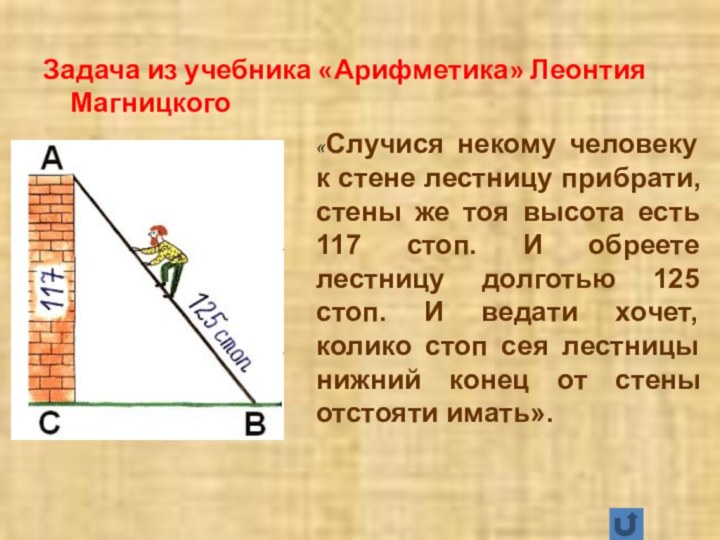
- 35. Задача из учебника «Арифметика» Леонтия Магницкого«Случися некому
- 36. Скачать презентацию
- 37. Похожие презентации
«Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора». Иоганн Кеплер


























Слайд 3
Закончите предложение:
Прямоугольным треугольником называется треугольник, у которого
один из углов равен ____
90°
Слайд 8 Если в треугольнике квадрат одной стороны равен сумме
квадратов двух других сторон , то такой треугольник –
____________
прямоугольный
Слайд 9
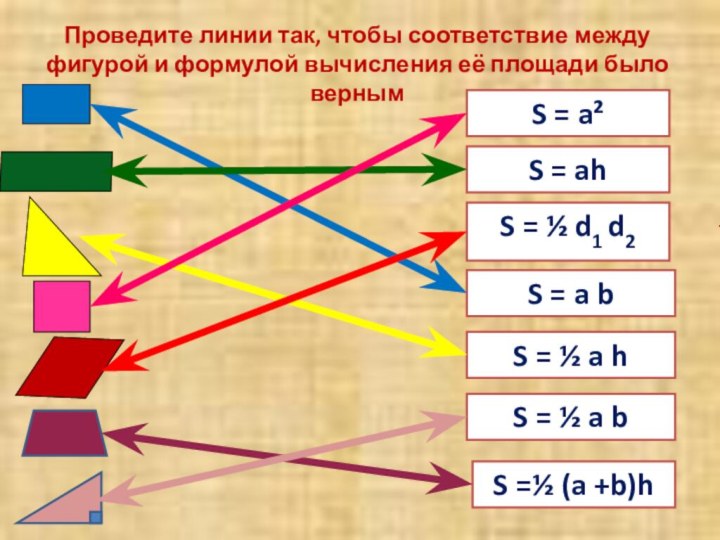
S = ½ d1 d2
S
= a²S = a b
S = ½ a h
S = ah
Проведите линии так, чтобы соответствие между фигурой и формулой вычисления её площади было верным
S =½ (a +b)h
S = ½ a b
Слайд 16
Задача
индийского математика XII века Бхаскары
"На берегу реки
рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь
упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?"Слайд 17 Из одной точки на земле отправились в путь
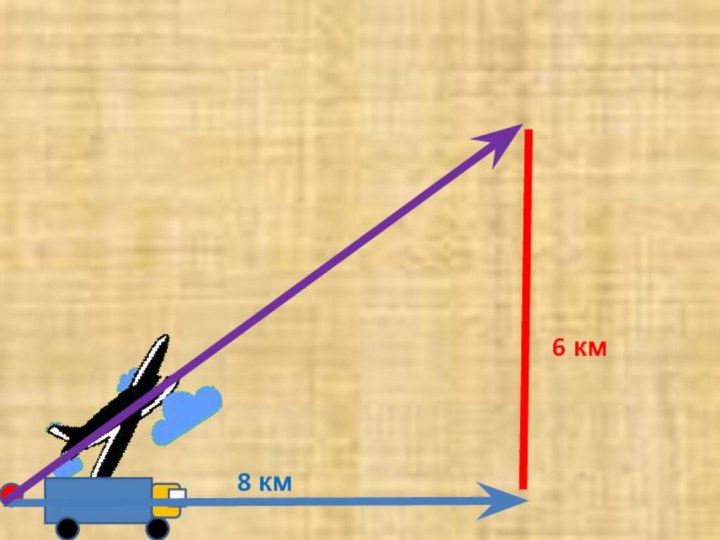
автомобиль и самолет . Автомобиль преодолел расстояние 8 км,
когда самолет оказался на высоте 6 км. Какой путь пролетел самолёт в воздухе с момента взлёта?Задача
Слайд 22
Дабы познать науки, Пифагор много путешествовал, в одной
из греческих колоний Южной Италии в городе Кротоне он
организовал кружок молодежи из представителей аристократии, куда принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Так возникла знаменитая«Пифагорейская школа».
Слайд 23 Пифагорейцы занимались математикой, философией, естественными науками. Ими было
сделано много важных открытий в арифметике и геометрии.
Однако,
в школе существовал Декрет, по которому авторство всех математических работ приписывалось Пифагору.Слайд 24 Пентаграмма – это звездчатый пятиугольник, который образован диагоналями
правильного пятиугольника.
Слайд 26
Доказательство теоремы Пифагора учащиеся средних веков
считали очень трудным и называли его Dons asinorum –
ослиный мост, или elefuga – бегство «убогих», так как некоторые «убогие» ученики, не имевшие серьёзной математической подготовки, бежали от геометрии. Слабые ученики, заучившие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста.Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли её также «ветряной мельницей», составляли стихи, вроде «Пифагоровы штаны на все стороны равны», рисовали карикатуры.
Немного истории
Слайд 28
Существует более 500 доказательств теоремы Пифагора
Доказательство с
помощью
мозаики
Древнекитайское
доказательство
Доказательство
Евклида
Древнеиндийское
доказательство
Слайд 31 Ещё землемеры Древнего Египта для построения прямого угла
использовали веревку, разделенную узлами
на 12 равных частей
Слайд 33
Правила написания синквейна:
-первая строка – одно слово
(существительное);
-вторая строка – два слова (прилагательные);
-третья строка
– три слова (глаголы );-четвертая строка – одно слово (существительное, отражающее Ваше отношение к тому, что написано в первой строке);
Напишите синквейн
по теме урока
Слайд 34
Теорема Пифагора – это одна из самых важных
теорем
геометрии. Значение её состоит в том, что
из неё
или с её помощью можно вывести большинство теорем геометрии.«Причина популярности теоремы Пифагора триедина - это красота, простота и значимость!»
Слайд 35
Задача из учебника «Арифметика» Леонтия Магницкого
«Случися некому человеку
к стене лестницу прибрати, стены же тоя высота есть
117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать».