- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку геометрии 7 класс на тему Признаки равенства треугольников
Содержание
- 2. Содержание
- 3. 1-й признак равенства треугольников (по двум сторонам
- 4. Дано:∆АВС; ∆А1В1С1АВ=А1В1
- 5. 2-й признак равенства треугольников (по стороне и
- 6. Дано:∆АВС; ∆А1В1С1АВ=А1В1 А =
- 7. 3-й признак равенства треугольников (по трем сторонам)Теорема:
- 8. 3-й признак – по трем сторонам (доказательство)Дано:∆АВС;
- 9. Задача № 1Дано: САDАС=АD; АВ=АЕДоказать:
- 10. Задача № 2Дано: DАС=
- 11. Задача № 3Дано: ∆АВС; ∆А1В1С1АМ=МС; А1М1=М1С1ВМ=В1М1АВ=А1В1; АС=А1С1Доказать:∆АВС=∆А1В1С1Доказательство:
- 12. Скачать презентацию
- 13. Похожие презентации






Слайд 3 1-й признак равенства треугольников (по двум сторонам и углу
между ними)
одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Слайд 4
Дано:
∆АВС; ∆А1В1С1
АВ=А1В1
АС=А1С1
А = А1
Доказать:
∆АВС = ∆А1В1С1
Доказательство:
1-й
признак – по двум сторонам и углу между ними (доказательство)Т.к. А= А1, то их можно наложить друг на друга,
отрезок АВ будет лежать на луче А1В1,
а отрезок АС – на луче А1С1.
Т.к. АВ=А1В1 и АС=А1С1, то точка В=В1 и точка С=С1, =>
ВС=В1С1 => ∆АВС = ∆А1В1С1
А
В
С
А1
В1
С1
=
=
=
Слайд 5 2-й признак равенства треугольников (по стороне и двум прилежащим
к ней углам)
Теорема:
Если сторона и два прилежащих к
ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Слайд 6
Дано:
∆АВС; ∆А1В1С1
АВ=А1В1
А = А1
В = В1
Доказать:
∆АВС =
∆А1В1С1Доказательство:
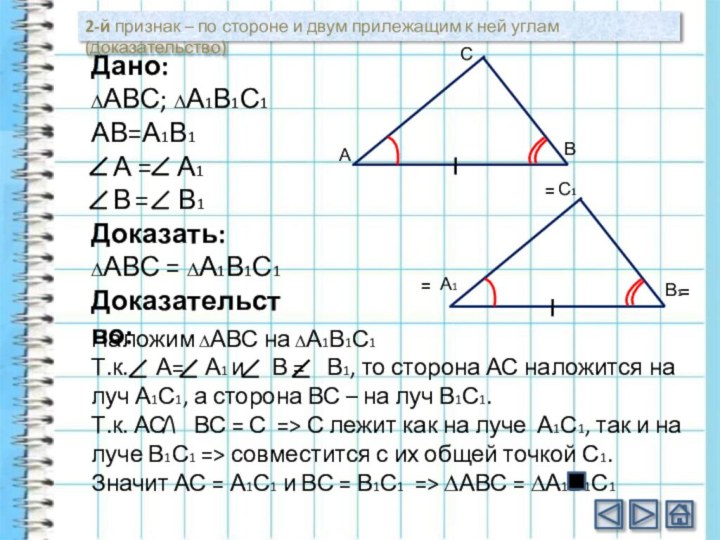
2-й признак – по стороне и двум прилежащим к ней углам (доказательство)
А
В
С
А1
В1
С1
Наложим ∆АВС на ∆А1В1С1
Т.к. А= А1 и В = В1, то сторона АС наложится на луч А1С1, а сторона ВС – на луч В1С1.
Т.к. АС ВС = С => С лежит как на луче А1С1, так и на луче В1С1 => совместится с их общей точкой С1.
Значит АС = А1С1 и ВС = В1С1 => ∆АВС = ∆А1В1С1
=
=
=
Слайд 7
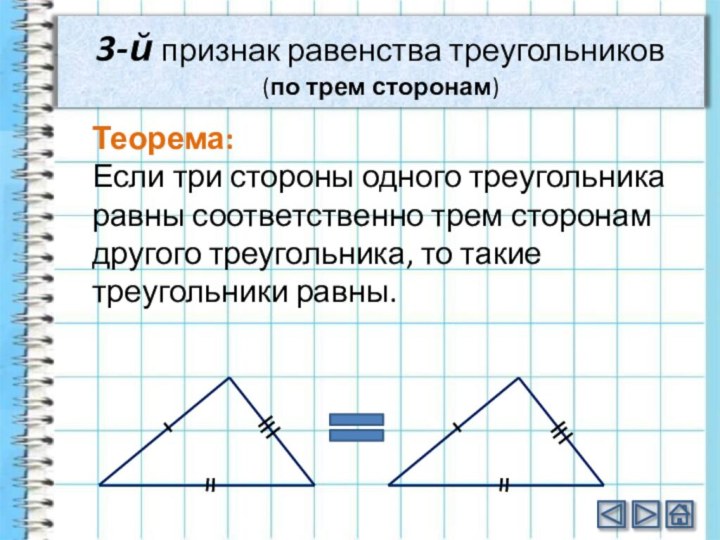
3-й признак равенства треугольников
(по трем сторонам)
Теорема:
Если три
стороны одного треугольника равны соответственно трем сторонам другого треугольника,
то такие треугольники равны.
Слайд 8
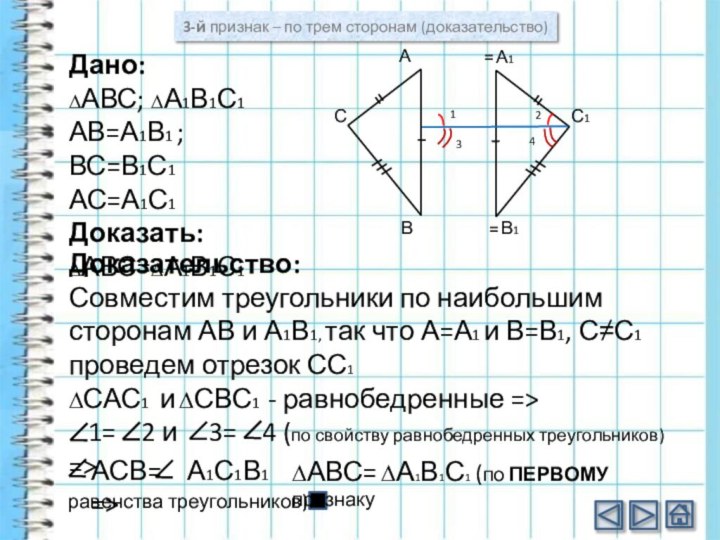
3-й признак – по трем сторонам (доказательство)
Дано:
∆АВС; ∆А1В1С1
АВ=А1В1
;ВС=В1С1
АС=А1С1
Доказать:
∆АВС=∆А1В1С1
Доказательство:
Совместим треугольники по наибольшим сторонам АВ и А1В1,
так что А=А1 и В=В1, С≠С1 проведем отрезок СС1
∆САС1 и ∆СВС1 - равнобедренные =>
1= 2 и 3= 4 (по свойству равнобедренных треугольников) =>
=
=
АСВ= А1С1В1 =>
∆АВС= ∆А1В1С1 (по ПЕРВОМУ признаку
равенства треугольников).
Слайд 9
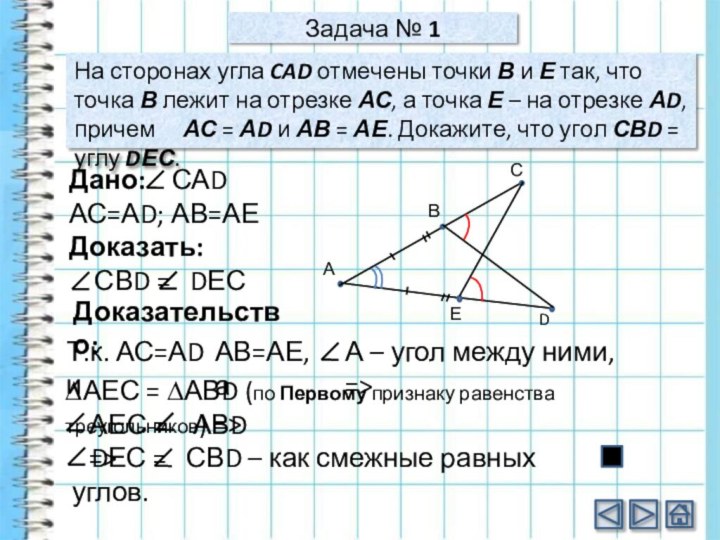
Задача № 1
Дано: САD
АС=АD; АВ=АЕ
Доказать:
СВD
= DЕС
Доказательство:
С
А
D
В
Е
Т.к. АС=АD и
АВ=АЕ, а
А – угол
между ними, => ∆АЕС = ∆АВD (по Первому признаку равенства треугольников) =>
АЕС = АВD =>
DЕС = СВD – как смежные равных углов.
На сторонах угла CAD отмечены точки В и Е так, что точка В лежит на отрезке АС, а точка Е – на отрезке АD, причем АС = АD и АВ = АЕ. Докажите, что угол СВD = углу DЕС.
Слайд 10
Задача № 2
Дано:
DАС=
DВС
АО=ВО
Доказать:
С = D;
АС=ВD
Доказательство:
Угол DAC =
углу DВС, АО = ВО. Докажите, что угол С = углу D и АС = ВD.
D
В
О
С
А
АОС = ВОD – как вертикальные =>
∆DОВ = ∆СОА (по Второму признаку равенства треугольников) =>
C= D
и АС=ВD
Слайд 11
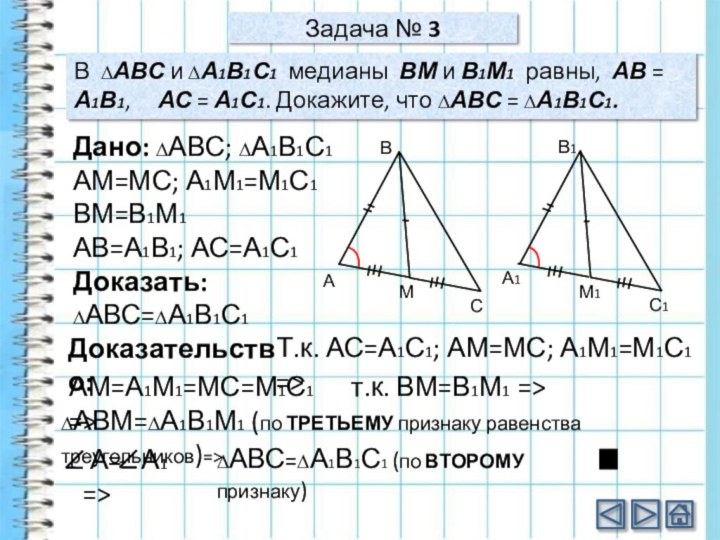
Задача № 3
Дано: ∆АВС; ∆А1В1С1
АМ=МС; А1М1=М1С1
ВМ=В1М1
АВ=А1В1; АС=А1С1
Доказать:
∆АВС=∆А1В1С1
Доказательство:
В
∆АВС и ∆А1В1С1 медианы ВМ и В1М1 равны, АВ
= А1В1, АС = А1С1. Докажите, что ∆АВС = ∆А1В1С1.А
В
С
А1
В1
С1
М
М1
Т.к. АС=А1С1; АМ=МС; А1М1=М1С1 =>
АМ=А1М1=МС=М1С1 =>
т.к. ВМ=В1М1 =>
∆АВМ=∆А1В1М1 (по ТРЕТЬЕМУ признаку равенства треугольников)=>
А= А1 =>
∆АВС=∆А1В1С1 (по ВТОРОМУ признаку)





























