Слайд 2
Введение
Трудно найти человека, у которого имя Пифагора не
ассоциировалось бы с его теоремой. Пожалуй, даже те, кто
в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах», - квадрате на гипотенузе, равновеликом двум квадратам на катетах.
Причина такой популярности теоремы Пифагора триедина: это npocтoma – кpacoта – значимость.
Слайд 3
В современных учебниках теорема сформулирована так: «В прямоугольном
треугольнике квадрат гипотенузы равен сумме квадратов катетов».
C
B
A
A2+B2=C2
Слайд 4
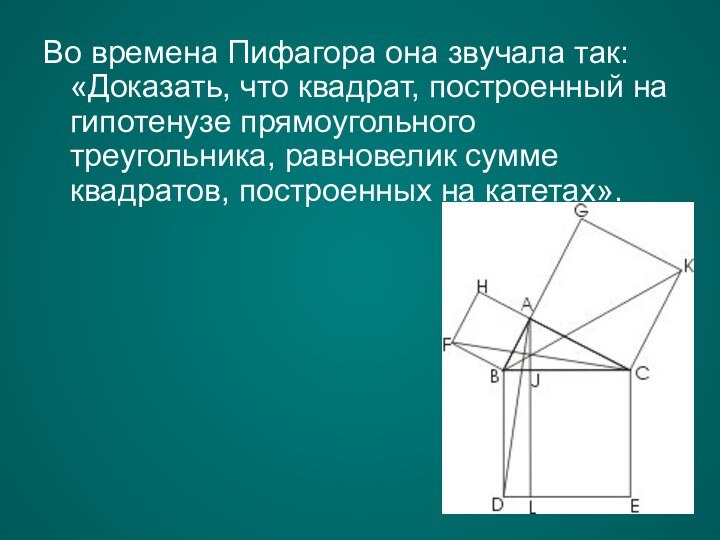
Во времена Пифагора она звучала так: «Доказать, что
квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов,
построенных на катетах».
Слайд 5
Цели и задачи проекта
Преподать содержание теоремы в более
простой и интересной форме;
Доступнее передать материал учебника используя дополнительные
средства информации;
Показать значение теоремы Пифагора в развитии науки и техники.
Слайд 6
«Золотые стихи» Пифагора
Будь справедлив и в словах ,
и в поступках своих…
(Пифагор)
Слайд 7
Пифагор, древнегреческий философ, религиозный и политический деятель, основатель
пифагореизма, математик, родился ок. 570 г. до н. э.
на острове Самосее в семье резчика по драгоценным камням. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Среди учителей юного Пифагора были старец Гермодамант и Ферекид Сиросский.
Пифагору приписывается изучение свойств целых чисел и пропорций, доказательство теоремы Пифагора и др. Страсть к музыке и поэзии великого Гомера Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом, окруженным толпой учеников, Пифагор начинал день с пения одной из песен Гомера. Воображению юного Пифагора очень скоро стало тесно на маленьком Самосе, и он отправляется в Милет, где встречается с другим ученым — Фалесом. По совету Фалеса Пифагор отправляется в Египет за знаниями.
Слайд 8
Несмотря на рекомендательное письмо фараона, хитроумные жрецы не

спешили раскрывать Пифагору свои тайны, предлагая ему сложные испытания.
Но влекомый жаждой к знаниям, Пифагор преодолел их все. Научившись всему, что дали ему жрецы, он двинулся на родину в Элладу. Пифагора не устраивала жизнь придворного полураба у правителя-тирана Поликрата, и он удалился в пещеры в окрестностях Самоса. Вскоре Пифагор переселяется в Кротон, где и задумывает создать собственную философскую школу.
Только в 60 лет, уже известный учёный Пифагор, всё ещё полный сил, полюбил одну из своих учениц – умницу и красавицу Теано. Последовательница его учения, она стала ему преданной женой и родила семерых детей.
Пифагор был очень счастлив в этом браке.
…Прошло 20 лет. Слава о братстве разнеслась по всему миру. Однажды к Пифагору приходит Килон, человек богатый, но злой, желая спьяну вступить в братство. Получив отказ, Килон начинает борьбу с Пифагором, воспользовавшись поджогом его дома. При пожаре пифагорейцы спасли жизнь своему учителю ценой своей, после чего Пифагор затосковал и вскоре покончил жизнь самоубийством.
Числа:
Числа, равные сумме своих делителей, воспринимались совершенными (6, 28, 496, 8128); дружественными называли пары чисел каждое из которых равнялось сумме делителей другого (220 и 184). Пифагор впервые разделил числа на четные и нечетные, простые и составные, ввел понятие фигурного числа.
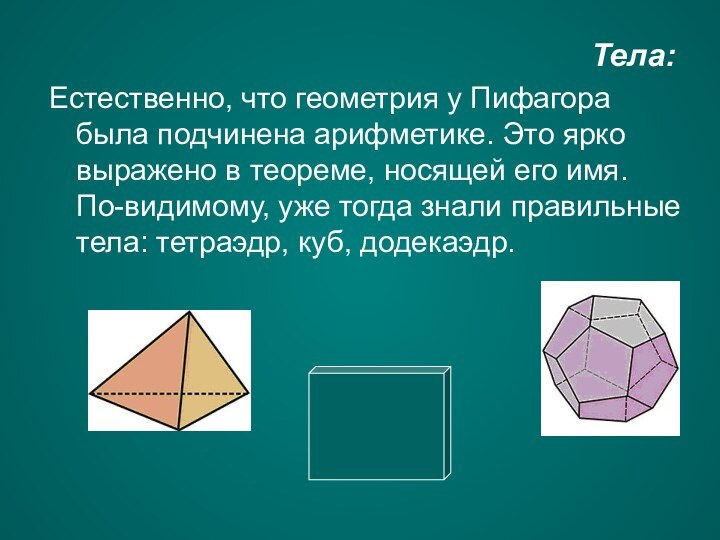
Тела:
Естественно, что геометрия у Пифагора была подчинена арифметике. Это ярко выражено в теореме, носящей его имя. По-видимому, уже тогда знали правильные тела: тетраэдр, куб, додекаэдр.
Слайд 11
Земля:
Следует заметить, что Пифагор считал Землю шаром,
движущимися вокруг солнца. Когда в XVI церковь начала преследовать
учение Коперника, это учение упорно именовалось пифагорейским.
Слайд 12
Музыка:
Музыка – точная наука. Пифагор внёс немалый
вклад в развитие теории музыки. Он задумывался над законами,
управляющими созвучием и диссонансом. Пифагор смастерил инструмент – балку со струнами, отягощёнными гирьками разного веса.
Слайд 13
Он выяснил, что колеблющиеся струны дают приятное для
слуха звучание, когда их длины соотносятся как 3:4:6 и
на основе этого вывел гармоничные музыкальные интервалы. Были получены простейшие созвучия: октава, квинта, кварта. Это позволило разработать теорию гармонических интервалов.
Слайд 14
Нравственные правила Пифагора
В античности Пифагор был известен более
всего как проповедник определённого образа жизни, что заключалось в
соблюдении некоторых правил:
«Не почитай знания за одно с мудростью».
«Тело своё не делай гробом души».
«Если не можешь иметь верного друга, будь сам себе другом».
«Не гоняйся за счастьем: оно всегда находится в тебе самом».
«Не делай никогда того, чего не знаешь. Но научись всему, что следует знать».
Слайд 15
За легендой – истина
Открытие теоремы Пифагора окружено
ореолом красивых легенд.
Слайд 16
Прокл, комментируя последнее предложение I книги «Начал» Евклида,
пишет: «Если послушать тех, кто любит повторять древние легенды,
то придётся сказать, что эта теорема восходит к Пифагору; рассказывают, что он в честь этого принёс в жертву 100 быков».
Слайд 17
Оптимист Михайло Ломоносов писал:
«Пифагор за изобретение одного
геометрического правила принёс на жертву сто волов. Но ежели
бы за найденные в нынешние времена от остроумных математиков правила по суеверной его ревности поступать, то едва бы в целом свете столько рогатого скота сыскалось».
Слайд 18
А ироничный Генрих Гейне видел развитие той же
ситуации несколько иначе: «Кто знает! Кто знает! Возможно, душа
Пифагора переселилась в беднягу, который не смог доказать теорему Пифагора и провалился из-за этого на экзаменах, тогда как в его экзаменаторах обитают души тех быков, которых Пифагор, обрадованный открытием теоремы, принёс в жертву бессмертным богам».
Слайд 19
История открытия теоремы
Обычно открытие теоремы Пифагора приписывают
древнегреческому философу и математику Пифагору, но изучение вавилонских клинописных
таблиц и древнекитайских рукописей показало, что это утверждение было известно задолго до Пифагора, а его заслуга состояла в том, что он открыл доказательства этой теоремы.
Слайд 20
В математической древнекитайской книге «Чу-пей» говорится о пифагоровом
треугольнике со сторонами 3, 4 и 5: «Если прямой
угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4».
В древнекитайском трактате «Чжоу – би суань цзинь» утверждается, что в XV в. до н. э. китайцы знали свойства египетского треугольника.
Слайд 21
Кантор (крупнейший немецкий историк математики) считает, что равенство
32+42=52 было известно уже египтянам ещё около 2300 г.
до н. э. во времена царя Аменемхета I.
Слайд 22
О теореме Пифагора знали и вавилоняне. В одном
тексте, относимом ко времени Хаммурапи, т.е. к 2000 г.
до н.э., приводится приближённое вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Междуречье умели производить вычисления с прямоугольными треугольниками.
Слайд 23
Доказательства
Существует около 500 различных доказательств этой теоремы. Вот
некоторые из них.
Школьное доказательство:
Рассмотрим прямоугольный треугольник c катетами а,
b и гипотенузой c. Докажем, что с2 = а2 + b2.
Достроим треугольник до квадрата со стороной a + b так, как показано на рисунке. Площадь S этого квадрата равна (а + b)2. C другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна 2ab, и квадрата со стороной c, поэтому
S = 4(1/2а2+с2)= 2ab + с2.
Таким образом, (а + b)2 = 2ab + с2, откуда
c2 = а2 + b2.
Слайд 24
Векторное доказательство:
Пусть АВС - прямоугольный треугольник с прямым
углом при вершине С, построенный на векторах. Тогда справедливо
векторное равенство: b + c = a, откуда имеем
c = a - b
возводя обе части в квадрат, получим
c² = a² + b² - 2ab
Так как a перпендикулярно b, то ab=0, откуда
c² = a² + b² или c² = a² + b²
Теорема доказана.
Слайд 25
Другие доказательства
Простейшее
Хоукинса
Вальдхейма
Гиппократа
Слайд 26
Метод дополнения
Метод вычитания
Слайд 27
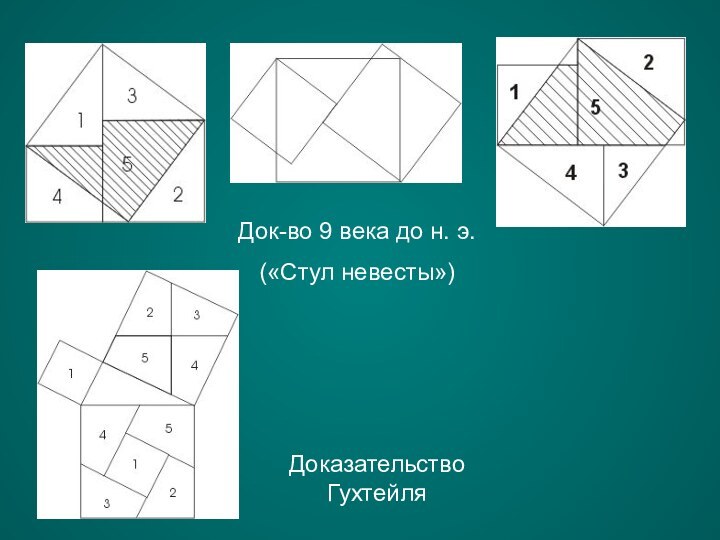
Док-во 9 века до н. э.
(«Стул невесты»)
Доказательство Гухтейля
Слайд 28
Значение и применение теоремы
Теорема Пифагора – это одна
из самых важных теорем геометрии. Значение её состоит в
том, что из неё или с её помощью можно вывести большинство теорем геометрии.
Теорема Пифагора была первым утверждением, связавшим длины сторон треугольников, потом узнали, как находить стороны и углы других треугольников. Возникла целая наука – тригонометрия, которая нашла применение в землемерии. Сейчас её применяют даже для измерения расстояний между космическими кораблями.
Знание теоремы позволяет находить высоту предмета и расстояния до недоступных объектов.
Подобные задачи решаются в повседневной жизни: строительстве и машиностроении при проектировании любых строительных объектов.
Слайд 29
Заключение
Основной метод, который я использовал в своей работе,
- это метод систематизации и обработки данных.
Используя информационные
технологии, я хотел разнообразить материал различными красочными иллюстрациями, привлекая внимание людей различных возрастов и профессий.
Практическое применение работы состоит в том, чтобы использовать мои знания и умения в методике преподавания алгебры и геометрии в школах.
Думаю, что моя работа стоит затраченных усилий.