результате изучения § 7 учащиеся должны знать теоремы о
среднем линии треугольника, о точке треугольника, о точке пересечения медиан треугольника; уметь их доказывать и применять к решению задач .Характеристика темы урока
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть















Характеристика темы урока
Цели урока
В
А
С
N
М
Доказательство.
Пусть дан Δ ABC и его средняя линия ED.
Проведем прямую параллельную стороне AB через точку D. По теореме Фалеса она пересекает отрезок AC в его середине, т.е. совпадает с DE.
Значит, средняя линия параллельна AB.
Проведем теперь среднюю линию DF.
Она параллельна стороне AC. Четырехугольник AEDF – параллелограмм.
По свойству параллелограмма ED=AF, а так как AF=FB по теореме Фалеса, то ED = ? AB. Теорема доказана.
С в о й с т в а
MN, MP, PN — средние линии треугольника ABC.
С в о й с т в а
№ 1
Ответ :
Да, является,
т.к. МК соединяет середины сторон треугольника АВС.
А
С
В
М
К
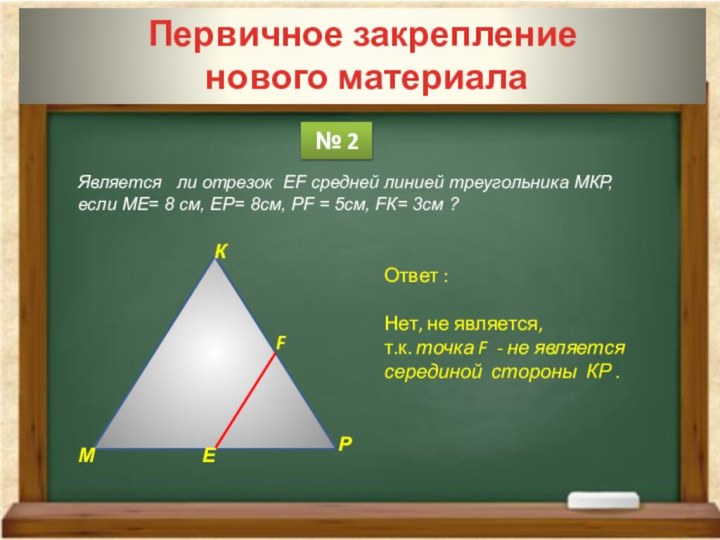
№ 2
Ответ :
Нет, не является,
т.к. точка F - не является серединой стороны КР .
М
К
Р
F
Е
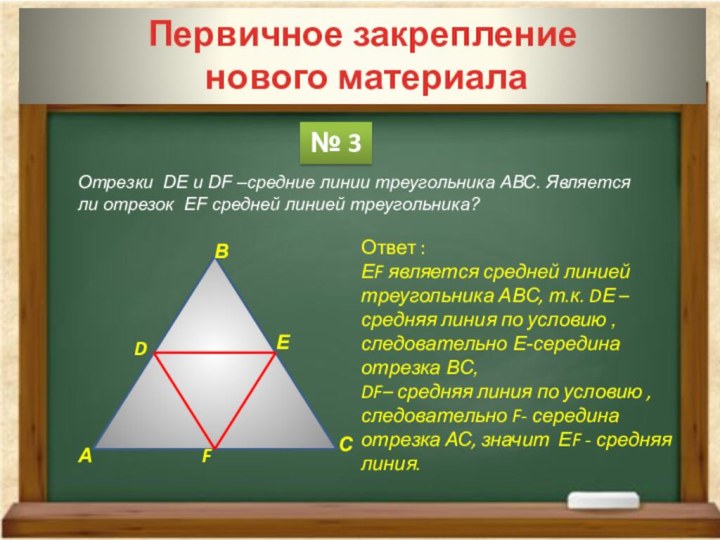
№ 3
Ответ :
ЕF является средней линией треугольника АВС, т.к. DЕ – средняя линия по условию , следовательно Е-середина отрезка ВС,
DF– средняя линия по условию , следовательно F- середина отрезка АС, значит ЕF - средняя линия.
А
В
С
Е
F
D
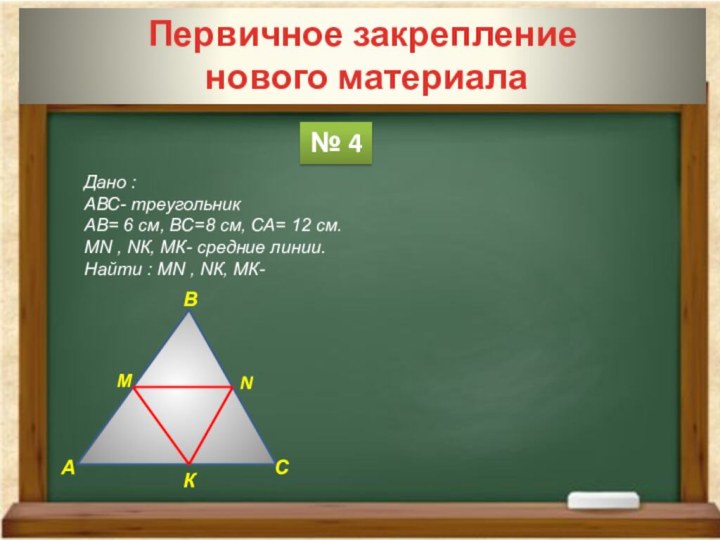
№ 4
А
М
В
N
С
К
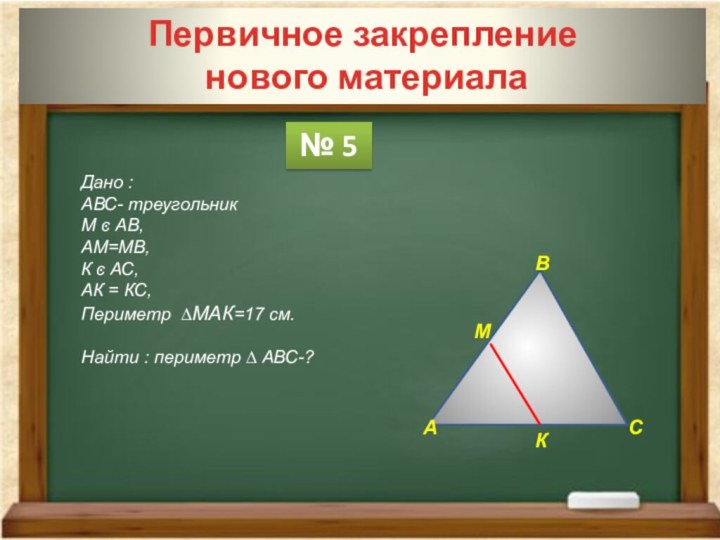
№ 5
А
М
В
С
К
№ 6
А
Е
В
С
F
Решение :
По свойству средней линии ∆ :
ЕF = ½ АС.
По условию: АС = ЕF + 7 см.
Следовательно, АС= ½ АС + 7 см,
Значит АС = 14 см.