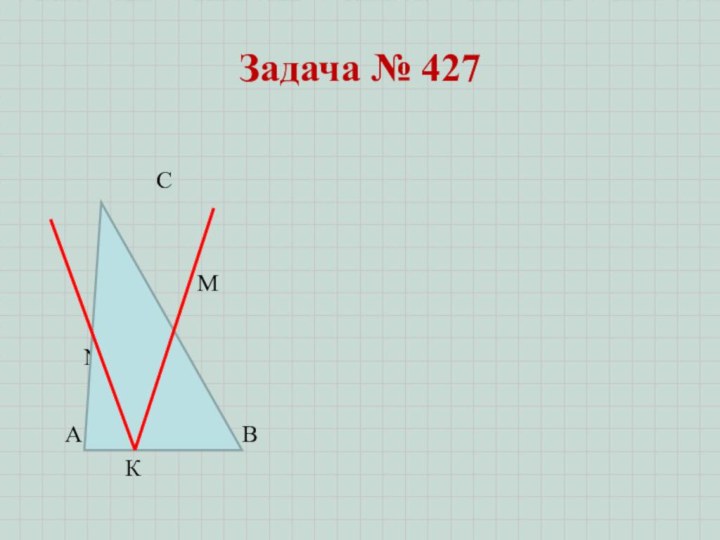
С
МN
A B
К
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Гл. 1. Урок 12. Осевая симметрия.
Содержание
- 2. Задача № 427
- 3. Осевая симметрияУчебная презентация
- 4. Симметрия – слово греческого происхождения: («сим» -
- 5. «Симметрия является той идеей, посредством которой человек
- 6. Симметричный рисунок окраски бабочки
- 7. Симметрия в природе
- 8. Симметричное расположение предметов
- 11. Симметрия в науке и технике
- 12. Симметрия в архитектуре
- 13. Симметрия в быту
- 14. Симметрия! Я гимн тебе пою!Тебя повсюду в
- 15. Какая фигура лишняя?
- 16. А1аОпределениеДве точки А и А1 называются симметричными
- 17. Фигуры, содержащие ось симметрии. Фигура называется
- 18. Фигуры, имеющие две оси симметрииПрямоугольник и ромб, не являющиеся квадратами, имеют две оси симметрии.
- 19. Фигуры, имеющие более двух осей симметрии Равносторонний треугольник
- 20. Фигуры, не имеющие осей симметрииК таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.
- 21. Это интересно!
- 22. В Е Ж З К Н О С Ф Х Э ЮБуквы, имеющие горизонтальную ось симметрии
- 23. А Д Ж Л М Н О П Т Ф Х ШБуквы, имеющие вертикальную ось симметрии
- 24. Симметрию можно увидеть в словах: казак, шалаш.
- 25. Самым ярким примером красоты форм осевой симметрии являются снежинки.
- 27. Скачать презентацию
- 28. Похожие презентации
Задача № 427 С М N A
Слайд 4 Симметрия – слово греческого происхождения: («сим» - с,
«метрон» - мера) и переводится как «соразмерность».
Соразмерность,
одинаковость в расположении частей по противоположным сторонам от точки, прямой или плоскости.Словарь С.И. Ожегова
Слайд 5 «Симметрия является той идеей, посредством которой человек на
протяжении веков пытался постичь и создать порядок, красоту и
совершенство».(Г. Вейль, немецкий математик)
Эпиграф к уроку
Слайд 14
Симметрия! Я гимн тебе пою!
Тебя повсюду в мире
узнаю.
Ты в Эйфелевой башне, ты в малой мошке,
Ты
в ёлочке, что у лесной дорожки.С тобою в дружбе и тюльпан, и роза,
И снежный рой – творение мороза.
Слайд 16
А1
а
Определение
Две точки А и А1 называются симметричными относительно
прямой а, если эта прямая проходит через середину отрезка
АА1 и перпендикулярна к нему
Слайд 17
Фигуры, содержащие ось симметрии.
Фигура называется симметричной
относительно прямой а, если для каждой точки фигуры симметричная
ей точка относительно прямой а также принадлежит этой фигуре.Такая фигура обладает осевой симметрией.
Слайд 18
Фигуры, имеющие две оси симметрии
Прямоугольник и ромб, не
являющиеся квадратами, имеют две оси симметрии.
Слайд 19
Фигуры, имеющие более двух осей симметрии
Равносторонний треугольник имеет
три оси симметрии, а квадрат – четыре оси симметрии.
У окружности бесконечно много осей симметрии – любая прямая, проходящая через её центр, является осью симметрии.
Слайд 20
Фигуры, не имеющие осей симметрии
К таким фигурам относятся
параллелограмм, отличный от прямоугольника, разносторонний треугольник.
Слайд 24
Симметрию можно увидеть в словах: казак, шалаш.
Такие
слова называются палиндромами. Ими увлекались многие поэты. Некоторые композиторы,
в том числе и великий Бах, писали музыкальные палиндромы. Но самые впечатляющие результаты дает симметрия в изобразительном искусстве.Есть целые фразы с таким свойством (если не учитывать пробелы между словами):
“Аргентина манит негра”,
“Искать такси”.
