Слайд 3
Внешний угол треугольника
Теорема о внешнем угле
треугольника:
Внешний угол треугольника равен сумме двух углов
не смежных с ним.
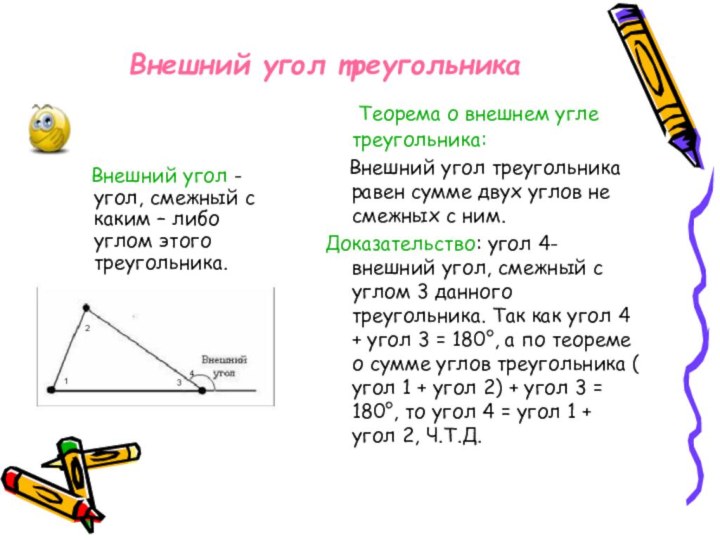
Доказательство: угол 4-внешний угол, смежный с углом 3 данного треугольника. Так как угол 4 + угол 3 = 180°, а по теореме о сумме углов треугольника ( угол 1 + угол 2) + угол 3 = 180°, то угол 4 = угол 1 + угол 2, Ч.Т.Д.
Внешний угол - угол, смежный с каким – либо углом этого треугольника.
Слайд 4
Виды треугольников
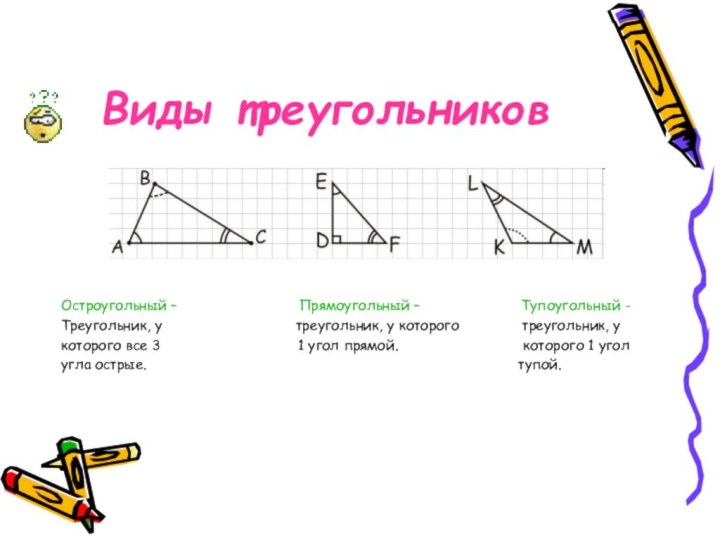
Остроугольный –
Прямоугольный – Тупоугольный -
Треугольник, у треугольник, у которого треугольник, у
которого все 3 1 угол прямой. которого 1 угол
угла острые. тупой.
Слайд 5
Теорема о соотношении между сторонами и углами треугольника.
Теорема о неравенстве треугольника.
Слайд 6
Прямоугольные треугольники
Сумма двух острых углов прямоугольного треугольника равна
90°;
Катет прямоугольного треугольника, лежащий против угла в 30°, равен
половине гипотенузы;
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета 30°.
Слайд 7
Признаки равенства прямоугольных треугольников
Если катеты одного прямоугольного треугольника
соответственно равны катетам другого, то такие треугольника равны;
Если катет
и гипотенуза одного треугольника соответственно равны катету и гипотенузе другого треугольника, то такие треугольники равны;
Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны;
Если катет и прилежащий к нему острый угол одного треугольника соответственно равны катету и прилежащему к нему острому другого, то такие треугольники равны.
Слайд 8
Расстояние от точки до прямой
Перпендикуляр, проведенный из точки
к прямой, меньше любой наклонной, проведённой из той же
точки к этой прямой;
Длина перпендикуляра, проведенного из точки к прямой называется расстоянием от этой точки до прямой.
Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.
Слайд 9
Расстояние между параллельными прямыми
Теорема.
Все точки каждой
из двух параллельных прямых равноудалены от другой прямой.
Слайд 10
Построение треугольника по трем сторонам
Задача. Построить треугольник по
трем сторонам a, b, с.
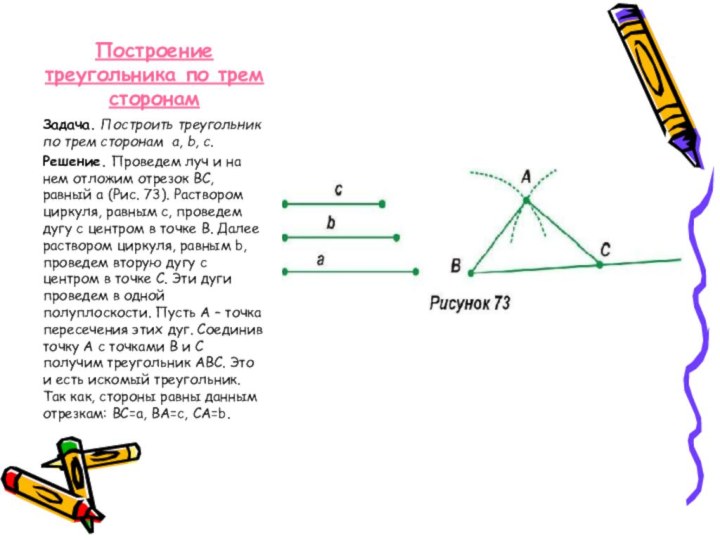
Решение. Проведем луч и
на нем отложим отрезок ВС, равный a (Рис. 73). Раствором циркуля, равным с, проведем дугу с центром в точке В. Далее раствором циркуля, равным b, проведем вторую дугу с центром в точке С. Эти дуги проведем в одной полуплоскости. Пусть А – точка пересечения этих дуг. Соединив точку А с точками В и С получим треугольник АВС. Это и есть искомый треугольник. Так как, стороны равны данным отрезкам: ВС=a, ВА=с, СА=b.
Слайд 11
Построение треугольника по двум сторонам и углу между
ними
Задача. Построить треугольник по двум сторонам и углу между
ними.
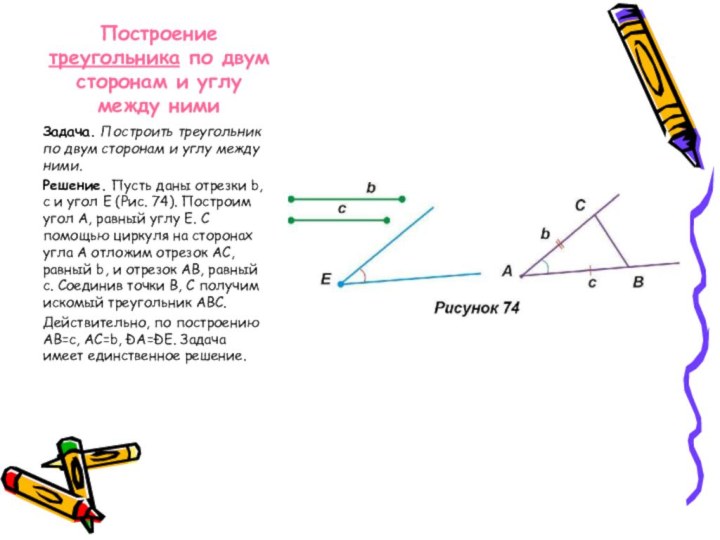
Решение. Пусть даны отрезки b, с и угол Е (Рис. 74). Построим угол А, равный углу Е. С помощью циркуля на сторонах угла А отложим отрезок АС, равный b, и отрезок АВ, равный с. Соединив точки В, С получим искомый треугольник АВС.
Действительно, по построению АВ=с, АС=b, ÐА=ÐЕ. Задача имеет единственное решение.
Слайд 12
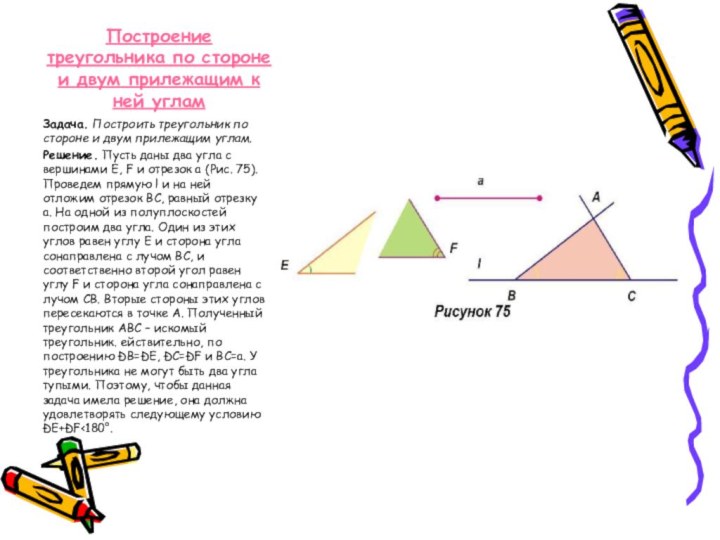
Построение треугольника по стороне и двум прилежащим к
ней углам
Задача. Построить треугольник по стороне и двум прилежащим
углам.
Решение. Пусть даны два угла с вершинами Е, F и отрезок a (Рис. 75). Проведем прямую l и на ней отложим отрезок ВС, равный отрезку a. На одной из полуплоскостей построим два угла. Один из этих углов равен углу Е и сторона угла сонаправлена с лучом ВС, и соответственно второй угол равен углу F и сторона угла сонаправлена с лучом СВ. Вторые стороны этих углов пересекаются в точке А. Полученный треугольник АВС – искомый треугольник. ействительно, по построению ÐВ=ÐЕ, ÐС=ÐF и ВС=a. У треугольника не могут быть два угла тупыми. Поэтому, чтобы данная задача имела решение, она должна удовлетворять следующему условию ÐЕ+ÐF<180°.