- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по стереометрии на тему Скрещивающиеся прямые
Содержание
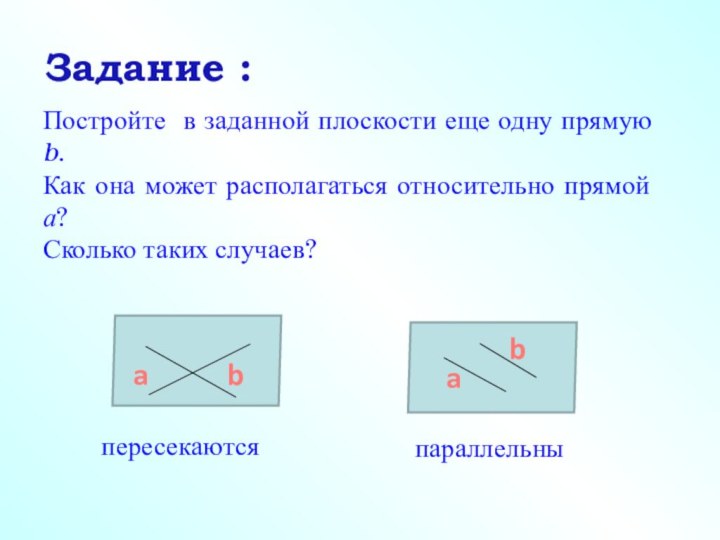
- 2. Разбейте данные рисунки по группам, найдя какой–либо признак для разделения.abaaabbЗадание:b123456
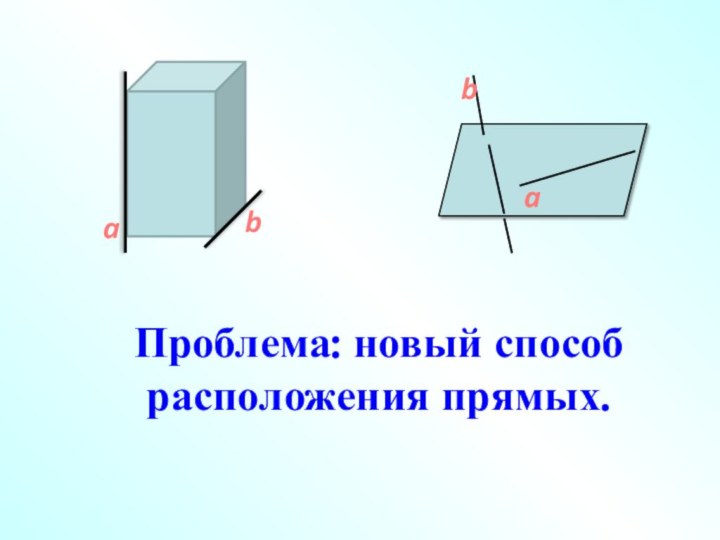
- 3. Проблема: новый способ расположения прямых.
- 4. Скрещивающиесяпрямые
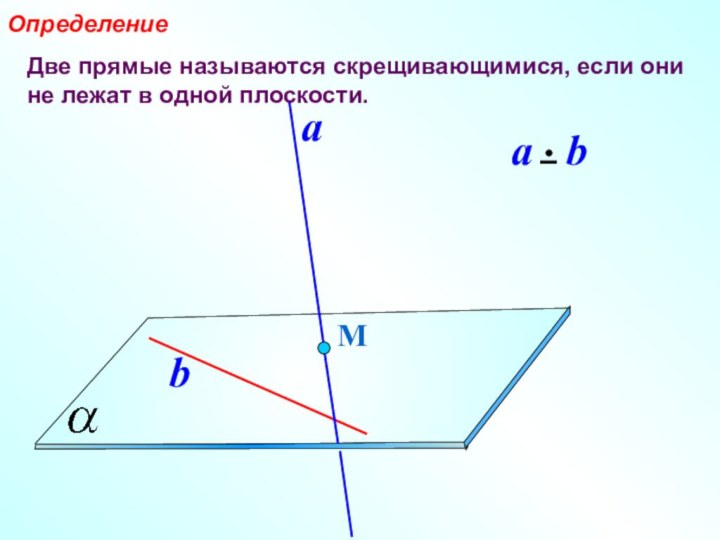
- 5. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.ОпределениеМab
- 6. abbbЗадание: найдите характерные особенности, которые позволяют отличить скрещивающиеся прямыеaa
- 7. IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIiНаглядное представление о скрещивающихся прямых дают две
- 8. ab
- 9. Если одна из двух прямых лежит в
- 10. а II bТри случая взаимного расположения двух прямых в пространствеМababab
- 11. Определить взаимное расположение прямых АВ1 и DC.
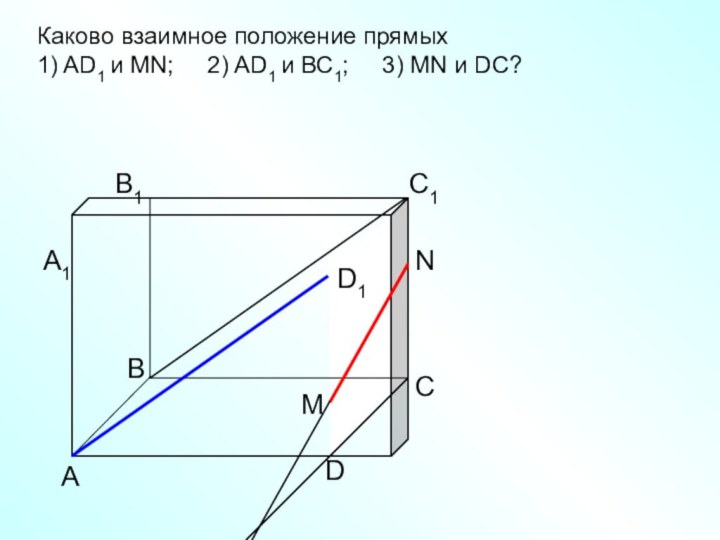
- 12. АDСВB1С1D1А1Каково взаимное положение прямых1) AD1 и МN;
- 13. Задача.αabМNДано: a || bMN ∩ a = MОпределитьвзаимное расположениепрямых MN u b.Скрещивающиеся.
- 14. Через вершину А ромба АВСD проведена прямая
- 15. АDСВB1С1D1А1Докажите, что прямые 1) AD и C1D1;
- 16. Задача АВСDMNPКДано: D (АВС),АМ =
- 17. Дано: точка А лежит вне плоскости DNK.Доказать: прямые AD и NK - скрещивающиесяАKNDЗадача №1
- 18. Дано: b|| BC, прямая а не принадлежит плоскости АВСДоказать: прямые a и b - скрещивающиесяbаАСВDГРУППА 2
- 19. ГРУППА 3АВСmУказать взаимное расположение прямых m и
- 20. Группа 4Дано:ABCD – квадратКА не лежит в (АВС)Определить взаимное расположение прямых КА и CDАКВСD
- 21. Группа 4
- 22. РЕФЛЕКСИЯ
- 23. Скачать презентацию
- 24. Похожие презентации
Разбейте данные рисунки по группам, найдя какой–либо признак для разделения.abaaabbЗадание:b123456












Слайд 6
a
b
b
b
Задание: найдите характерные особенности,
которые позволяют отличить
скрещивающиеся
прямые
a
a
Слайд 7
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIi
Наглядное представление о скрещивающихся прямых дают две дороги,
одна из которых проходит по эстакаде, а другая под
эстакадой.
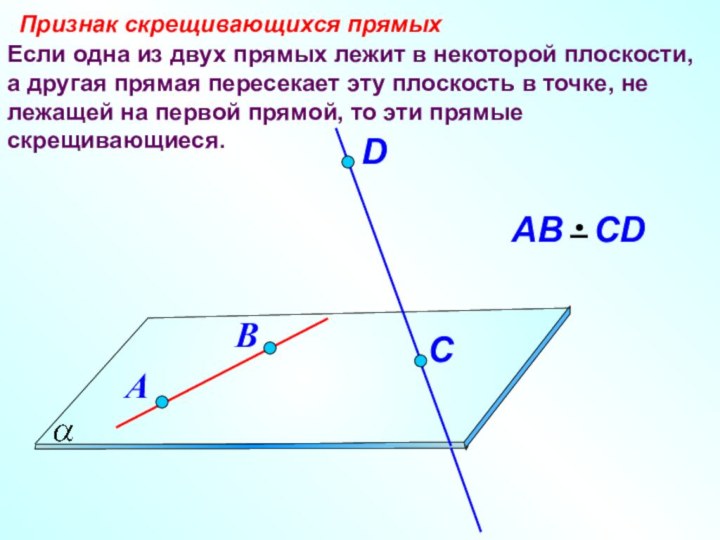
Слайд 9 Если одна из двух прямых лежит в некоторой
плоскости, а другая прямая пересекает эту плоскость в точке,
не лежащей на первой прямой, то эти прямые скрещивающиеся.Признак скрещивающихся прямых
D
В
А
C
Слайд 13
Задача.
α
a
b
М
N
Дано: a || b
MN ∩ a = M
Определить
взаимное
расположение
прямых MN u b.
Скрещивающиеся.
Слайд 14
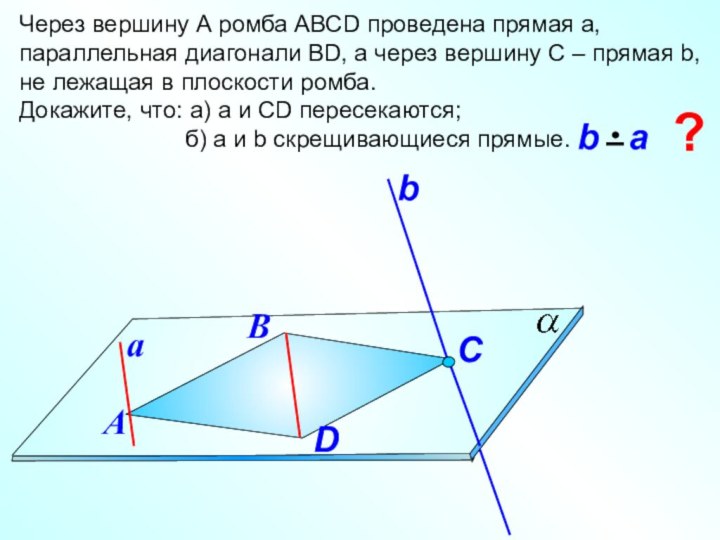
Через вершину А ромба АВСD проведена прямая а,
параллельная диагонали ВD, а через вершину С – прямая
b, не лежащая в плоскости ромба.Докажите, что: а) а и СD пересекаются;
б) а и b скрещивающиеся прямые.
В
А
C
?
a
D
Слайд 15
А
D
С
В
B1
С1
D1
А1
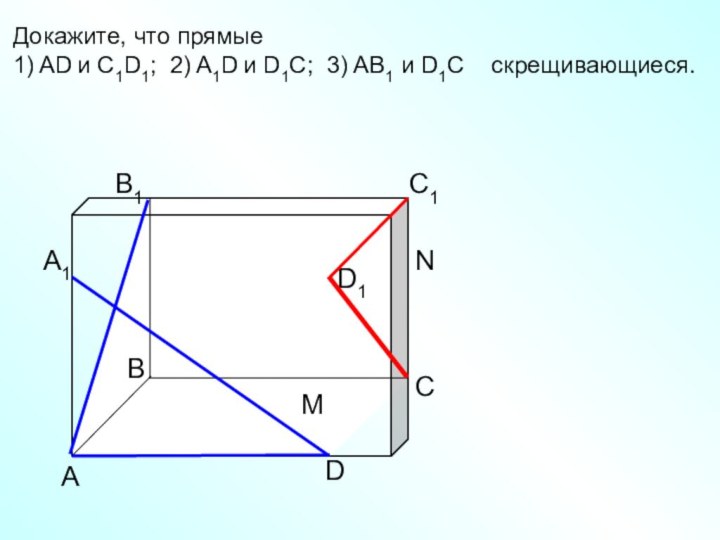
Докажите, что прямые
1) AD и C1D1; 2)
A1D и D1C; 3) AB1 и D1C скрещивающиеся.
N
M
Слайд 16
Задача
А
В
С
D
M
N
P
К
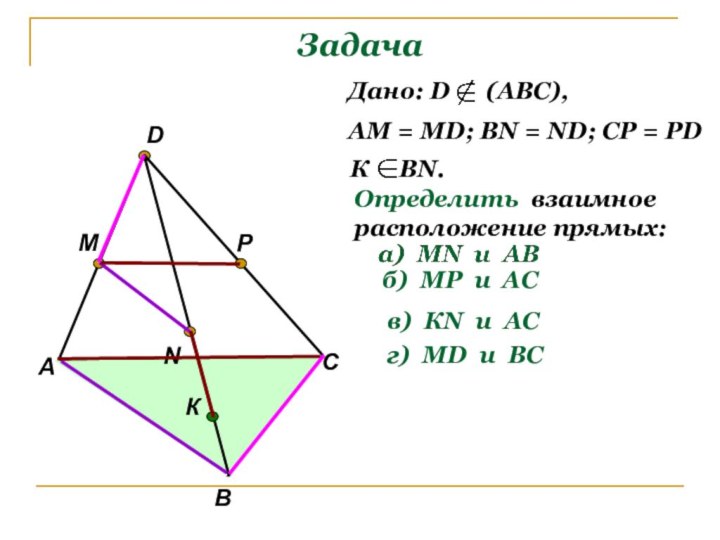
Дано: D (АВС),
АМ = МD;
ВN = ND; CP = PD
К ВN.
Определить
взаимное расположение прямых:
б) МР и AС
в) КN и AС
г) МD и BС
Слайд 17
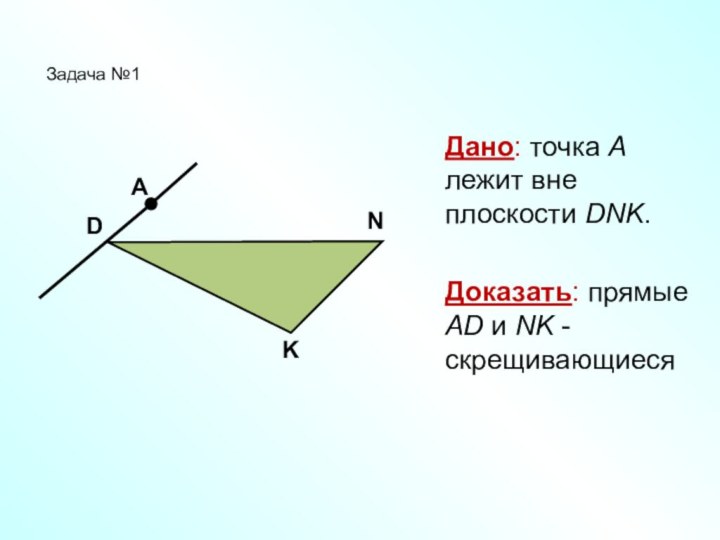
Дано: точка А лежит вне плоскости DNK.
Доказать: прямые
AD и NK - скрещивающиеся
А
K
N
D
Задача №1
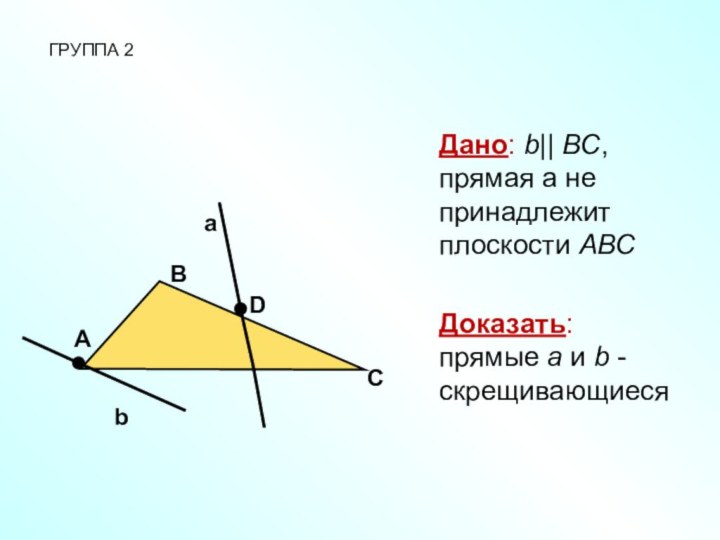
Слайд 18 Дано: b|| BC, прямая а не принадлежит плоскости
АВС
Доказать: прямые a и b - скрещивающиеся
b
а
А
С
В
D
ГРУППА 2
Слайд 19
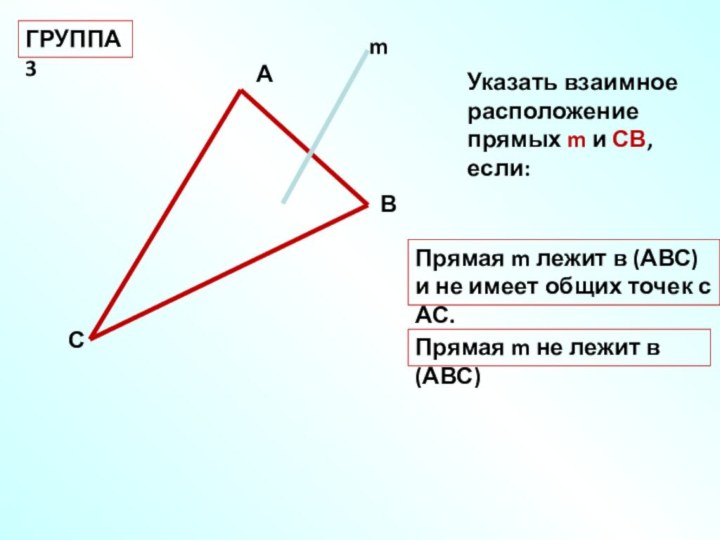
ГРУППА 3
А
В
С
m
Указать взаимное расположение прямых m и СВ,
если:
Прямая m лежит в (АВС) и не имеет общих
точек с АС.Прямая m не лежит в (АВС)