Слайд 2
Содержание
Золотое сечение – гармоническая пропорция.
История Золотого сечения.
Деление
отрезка в золотом отношении.
Золотой треугольник.
Золотой прямоугольник.
Пентаграмма.
Золотой прямоугольный треугольник.
Золотой эллипс.
Золотое
сечение в природе.
Пропорция и Золотое сечение во внешних формах человека.
Золотое сечение в живописи.
Золотое сечение в архитектуре и скульптуре .
Золотое сечение в поэзии.
Золотое сечение в музыке.
Слайд 3
Золотое сечение -
гармоническая пропорция
Слайд 4
Математическое понимание гармонии
Гармония – связь, созвучие, соразмерность,
согласованность частей одного целого.
Математическая гармония - это равенство или
соразмерность частей друг c другом и части с целым.
Понятие математической гармонии тесно связано с понятиями пропорции и симметрии.
Слайд 5
Золотое сечение – гармоническая пропорция
Пропорция (от лат.
proportio) означает «соразмерность», «определенное соотношение частей между собой».
В
математике пропорцией называют равенство двух отношений:
a : b = c : d.
Слайд 6
Отрезок прямой АВ можно разделить на две части
следующими способами:
а) на две равные части;
б) на две неравные
части в любом отношении (такие части пропорции не образуют);
в) таким образом, когда АВ : АС= АС : ВС.
Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.
АВ : АС = АС: ВС
А
А
А
С
С
С
В
В
В
а)
б)
в)
Слайд 7
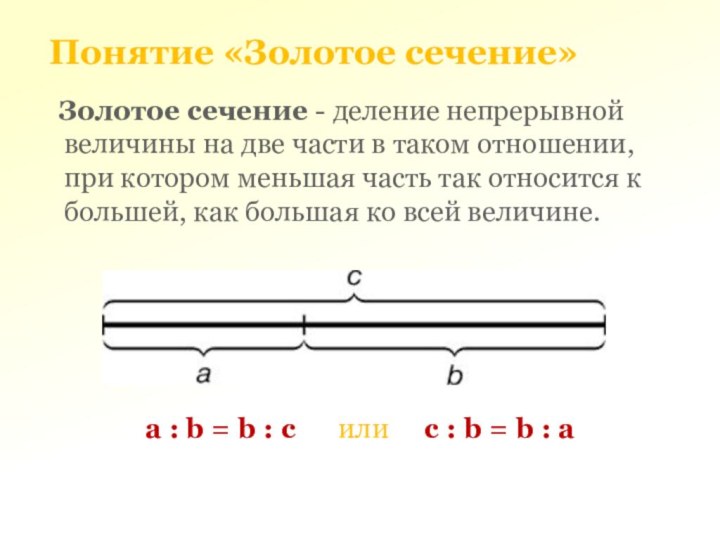
Понятие «Золотое сечение»
a : b = b :
c или с : b
= b : а
Золотое сечение - деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.
Слайд 8
Эта пропорция равна:
Золотое сечение в процентах
Слайд 10
История «Золотого сечения»
Понятие о золотом делении ввел в
научный обиход Пифагор, древнегреческий философ и математик (VI в.
до н.э.)
В Древнем Египте существовала «система правил гармонии», основанная на Золотом Сечении.
В Древней Греции Золотое Сечение было своеобразным каноном культуры, который пронизывает все сферы науки и искусства. Красота и гармония стали важнейшими категориями познания.
В толковании древних греков понятие золотого сечения, и понятие гармонии идентичны.
Согласно Пифагору гармония имеет численное выражение, то есть, она связана с концепцией числа.
Евклид излагает теорию Платоновых тел, которая является существенным разделом геометрической теории Золотого Сечения.
Теория гармонии Древних
Слайд 12
а) тетраэдр («Огонь»), б) гексаэдр («Земля»),
в) октаэдр
(«Воздух»),
г) икосаэдр («Вода»),
д) додекаэдр («Вселенский разум»).
Платоновы тела:
Слайд 13
Ряд Фибоначчи
С историей золотого
сечения связано имя итальянского
математика Леонардо Фибоначчи.
Ряд чисел
0, 1, 1, 2,
3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи.
Слайд 14
«Золотая Пропорция» - главный эстетический принцип эпохи Средневековья
Леонардо
да Винчи(1452-1519) художник и ученый был одним из первых,
кто ввел сам термин «Золотое Сечение».
Доказано, что во многих своих произведениях Леонардо да Винчи использовал пропорции золотого сечения, в частности, в своей всемирно известной фреске «Тайная вечеря» и непревзойденной «Джоконде.
«Пусть никто, не будучи математиком, не дерзнет читать мои труды». Леонардо да Винчи.
Слайд 15
«Витрувианский человек» Леонардо да Винчи
Слайд 16
Пропорции человеческого тела (Витрувий)
длина от кончика самого длинного
до самого низкого основания из четырёх пальцев равна ладони
ступня
составляет три ладони
локоть составляет шесть ладоней
высота человека составляет четыре локтя (и соответственно 24 ладони)
шаг равняется четырём ладоням
размах человеческих рук равен его высоте
расстояние от линии волос до подбородка составляет 1/10 его высоты
расстояние от макушки до подбородка составляет 1/8 его высоты
расстояние от макушки до сосков составляет 1/4 его высоты
максимум ширины плеч составляет 1/4 его высоты
расстояние от локтя до кончика руки составляет 1/4 его высоты
расстояние от локтя до подмышки составляет 1/8 его высоты
длина руки составляет 2/5 его высоты
расстояние от подбородка до носа составляет 1/3 длины его лица
расстояние от линии волос до бровей 1/3 длины его лица
длина ушей 1/3 длины лица
пупок является центром окружности
Слайд 17
Лука Пачоли ( 1445 —19 июня 1517) итальянский математик.
В
1509 г. в Венеции была издана книга Пачоли «Божественная
пропорция».
Слайд 18
Дюрер:
«Необходимо, чтобы тот, кто что-либо умеет, обучил этому
других, которые в этом нуждаются. Это я и вознамерился
сделать».
Альбрехт Дюрер (1471-1528)- выдающийся немецкий художник и теоретик искусства эпохи Возрождения.
Слайд 19
Вклад Кеплера
в теорию Золотого Сечения
Иоганн Кеплер (1571-1630)-астроном,
приверженец Золотого Сечения.
Кеплер обратил внимание на ботаническую закономерность филлотаксиса
и установил связь между числами Фибоначчи и золотой пропорцией, доказав, что последовательность отношений соседних чисел Фибоначчи:
1/1; 2/1; 3/2; 5/3 ;8/5; 13/8;…в пределе стремится к золотой пропорции.
«Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора , а другое – деление отрезка в среднем и крайнем отношении… Первое можно сравнивать с мерой золота ; второе же больше напоминает - драгоценный камень.»
Слайд 21
Дано: отрезок АВ.
Построить: золотое сечение отрезка АВ,
т.е. точку Е так, чтобы
Деление отрезка в золотом отношении
Построение.
1) Построим прямоугольный треугольник, у которого один катет в два раза больше другого. Для этого восстановим в точке В перпендикуляр к прямой АВ и на нем отложим отрезок ВС= .
2) Далее, соединим точки А и С, отложим отрезок CD=CB,
3) Отложим AE=AD.
Точка Е является искомой,
она производит золотое
сечение отрезка АВ.
Слайд 22
А
В
С
Золотым называется такой равнобедренный треугольник, основание и боковая
сторона которого находятся в золотом отношении:
Золотой треугольник
Слайд 24
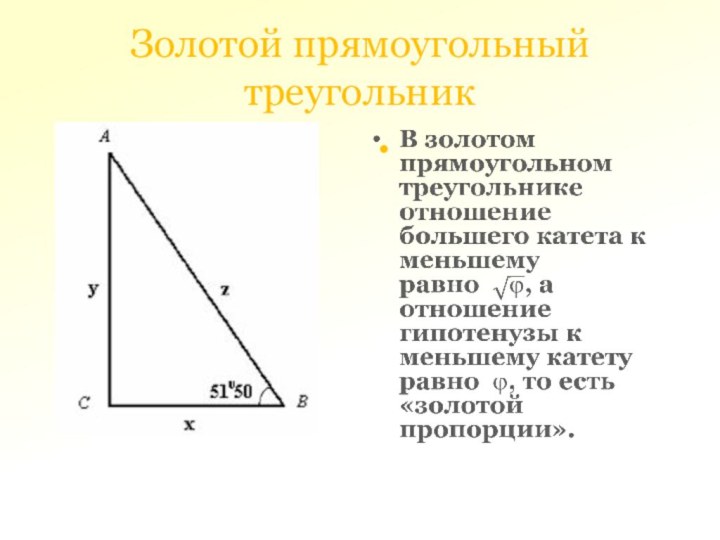
Золотой прямоугольный треугольник
Слайд 25
Прямоугольник, стороны которого находятся в золотом отношении, т.е.
отношение длины к ширине даёт число φ, называется золотым
прямоугольником.
Золотой прямоугольник
Слайд 26
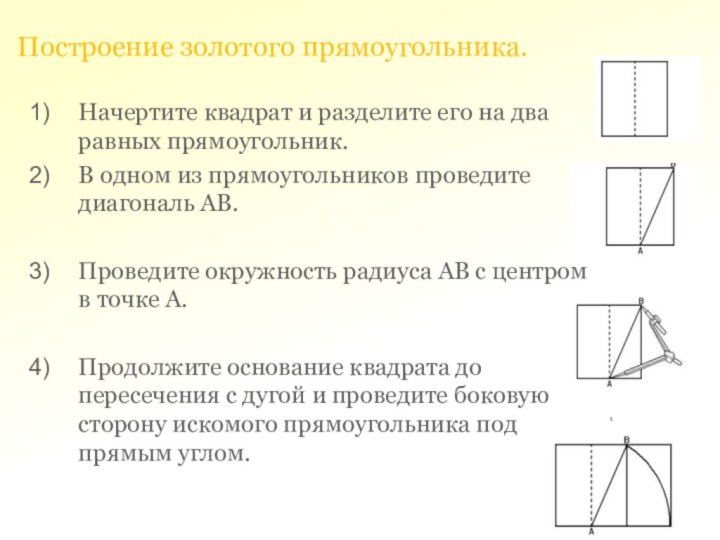
Начертите квадрат и разделите его на два равных
прямоугольник.
В одном из прямоугольников проведите диагональ АВ.
Проведите окружность радиуса
АВ с центром в точке А.
Продолжите основание квадрата до пересечения с дугой и проведите боковую сторону искомого прямоугольника под прямым углом.
Построение золотого прямоугольника.
Слайд 27
Золотой эллипс
Золотой эллипс формируется с помощью двух ромбов ACBD
и ICJD, вписанных в эллипс . Золотые ромбы ACBD
и ICJD состоят из
4-х прямоугольных треугольников типа OCB или OCJ, которые являются золотыми прямоугольными треугольниками.
Слайд 28
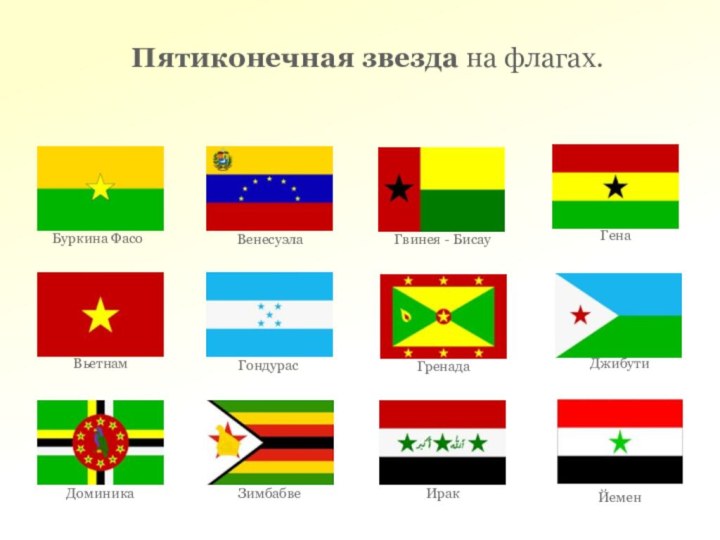
Пентаграмма
Если в пентаграмме провести все диагонали, то в
результате получим пятиугольную звезду.
Точки пересечения диагоналей в пентаграмме
являются точками золотого сечения диагоналей (отношение синего отрезка к зелёному, красного к синему, зелёного к фиолетовому, равны 1.618). При этом эти точки образуют новую пентаграмму FGHKL и пять правильных треугольников (ADC, ADB,EBD, AEC,EBC)
Слайд 31
Раифский мужской монастырь.
«Пентагон» США.
Слайд 33
Вопрос:
Что общего в молекулах ДНК, кристаллах снежинок,
лепестков розы, раковин моллюсков, рогов млекопитающих, далеких космических галактиках?
Слайд 34
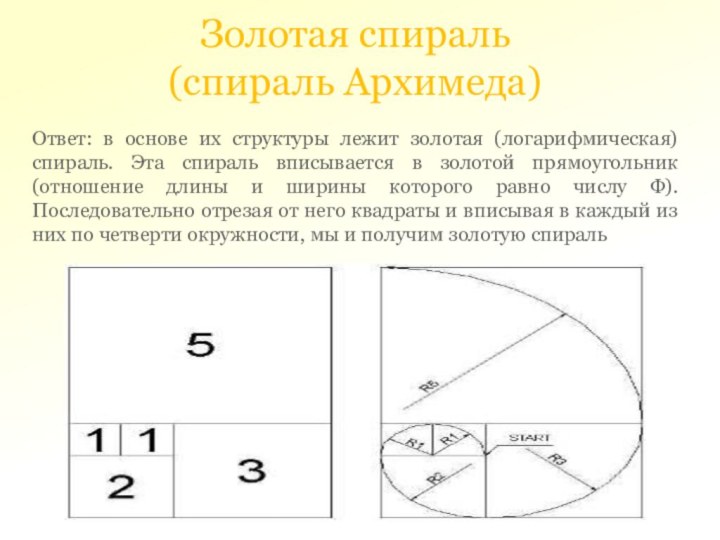
Золотая спираль (спираль Архимеда)
Ответ: в основе их структуры
лежит золотая (логарифмическая) спираль. Эта спираль вписывается в золотой
прямоугольник (отношение длины и ширины которого равно числу Ф). Последовательно отрезая от него квадраты и вписывая в каждый из них по четверти окружности, мы и получим золотую спираль
Слайд 35
Явление филлотаксиса
Филлотаксисом называется своеобразное решетчатое расположение листьев, семян,
чешуек многих видов растений.
Ряды ближайших соседей в таких решетках
разворачиваются по спиралям или закручиваются винтовыми линиями вокруг цилиндра.
Семечки в подсолнухе расположены по логарифмическим спиралям. При этом отношение числа левых и правых спиралей равно отношению соседних чисел Фибоначчи . Можно встретить подсолнухи с отношением количества спиралей 34 /55 и 55/89.
Слайд 36
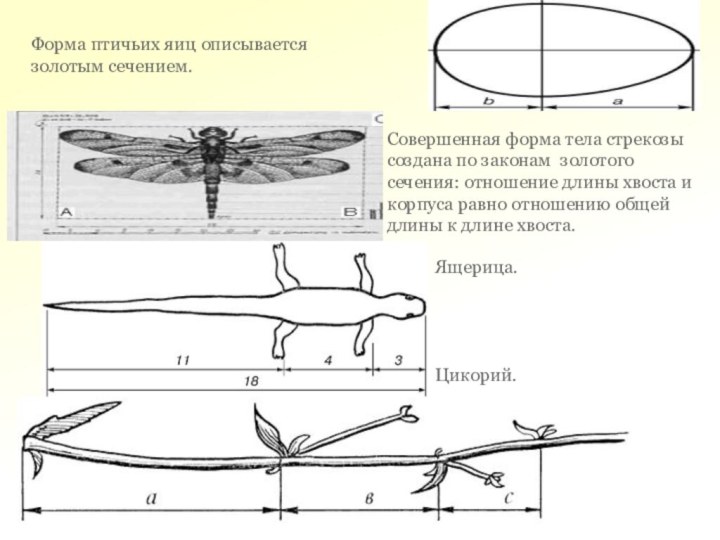
Форма птичьих яиц описывается золотым сечением.
Совершенная форма
тела стрекозы создана по законам золотого сечения: отношение длины
хвоста и корпуса равно отношению общей длины к длине хвоста.
Ящерица.
Цикорий.
Слайд 37
Золотое сечение
и пропорция во внешних
Формах человека.
«Обнаженное тело кажется мне прекрасным.
Для меня оно – чудо, где не может быть ничего безобразного»
О.
Роден.
Слайд 38
Цейзинг:
Мужское тело:
13 : 8 = 1,625
Женское
тело:
8 : 5 = 1,6.
У новорожденного: 1
: 1.
Слайд 39
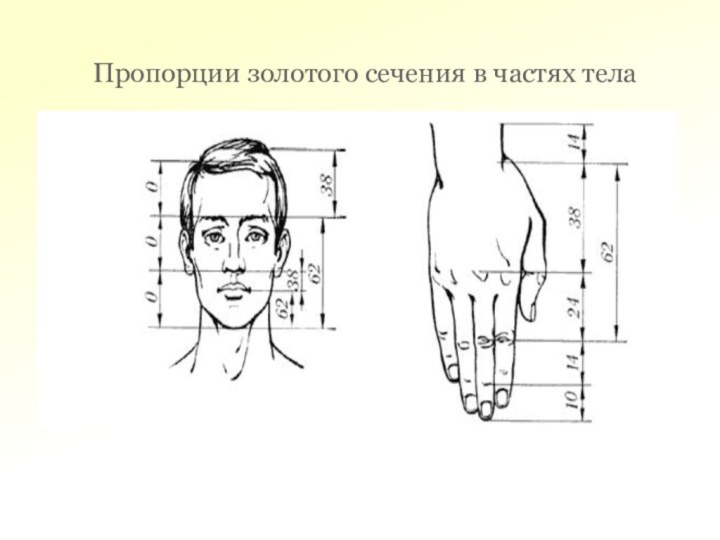
Пропорции золотого сечения в частях тела
Слайд 40
Скульптурный портрет Нефертити и его гармонический анализ,
выполненный
Э.М. Сороко.
Слайд 41
Гармонический анализ женского лица.
Н.И. Крюковский :
"Созерцая совершенное, прекрасное
человеческое лицо и тело, невольно приходишь к мысли о
каком-то скрытом, но явственно чувствующемся математическом изяществе его форм, о математической правильности и совершенстве составляющих его криволинейных поверхностей!"
Слайд 42
Золотое сечение
в живописи
«Поистине живопись – наука и
законная дочь природы…»
Леонардо да Винчи
Слайд 43
В эпоху Возрождения художники открыли, что любая
картина имеет определенные точки, невольно приковывающие наше внимание, так
называемые зрительные центры . Таких точек всего четыре, и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости.
«Золотое сечение»
картины.
Слайд 44
Золотое сечение в картине Леонардо да Винчи "Джоконда"
Слайд 45
Портрет Моны Лизы привлекает тем, что композиция рисунка
построена на «золотых треугольниках».
Слайд 46
Существовало мнение, что композиция имеет успех из-за построения
на «золотых прямоугольниках».
Слайд 47
Существовало мнение, что композиция имеет успех из-за построения
на «золотых прямоугольниках».
Слайд 48
Картина имеет точки, невольно приковывающие наше внимание, так
называемые зрительные центры..
Слайд 49
Фреска Леонардо да Винчи
«Тайная вечеря» и
золотое сечение
Слайд 50
На фреске «Тайная вечеря» четко просматривается деление картины
в пропорциях золотого сечения.
Слайд 51
Наличие золотых прямоугольников
Слайд 53
На фреске «Тайная вечеря» четко просматривается наличие золотого
прямоугольника
Слайд 54
В композиции фрески «Тайная вечеря» можно обнаружить наличие
золотых треугольников.
Слайд 55
Золотое сечение в картине
И.И. Шишкина «Корабельная роща»
Слайд 56
На знаменитой картине И.И. Шишкина «Корабельная роща» с
очевидностью просматриваются мотивы золотого сечения.
Слайд 57
Золотые треугольники
и композиция картины
Слайд 58
Сандро Ботичелли «Рождение
Венеры» (около 1485 г).
Пропорции Венеры выполнены в золотом сечении.
Слайд 59
Золотая спираль в картине Рафаэля"Избиение младенцев»
«Золотая спираль» выбрана
как композиционная основа рисунка Рафаэля.
Слайд 60
К.А. Васильев «У окна»
Суд Париса Камея
Иванов
«Явление Христа
народу»
Слайд 61
Золотое сечение
в архитектуре
и скульптуре
Гармония – вот
что лежит в основе всех видов искусства на всем
протяжении человеческой истории.
И.В.Жолтовский
Слайд 62
Парфенон – главный храм
Афинского Акрополя.
Архитектор Фидий
Слайд 63
Афинский Акрополь – Золотое сечение
Слайд 64
Покровский Собор на Красной
Площади в Москве.
Собор
Нотр-дам де Пари
в Париже.
Слайд 65
Церковь Покрова Богородицы на Нерли 1165 год
«Простая» красота пропорций золотого сечения.
Слайд 66
М.Ф. Казаков. Сенат.Разрез.(парадный зал).Фрагмет проекта. Москва (1776-1782)
Слайд 67
Голицинская больница.Москва.1794-1801. Фасад
М.Ф.Казаков. Голицынская больница. Москва. 1794-1801гг
Слайд 68
Петровский дворец.(1776 –1796 ).
Военно-воздушная академия.
Слайд 69
В.И.Баженов. Дом – Пашкова. Москва.1786г.
Слайд 70
Золотое сечение в скульптуре
Венера Милосская
Дорифор Поликлета
Слайд 71
Моисей. Скульптура Микеланджело(1515г.)
Слайд 72
Аполлон Бельведерский.Скульптор Леохара
(середина V века до н.э.)
Слайд 74
Афина Парфенос.Скульптор Фидий(Vвек до н.э.)
Слайд 75
Золотое сечение
в поэзии и музыке
Все, что пишется
с божественным вдохновением и святым духом, то весьма прекрасно.
Демокрит.
Слайд 76
Результаты исследования золотого сечения в музыке
впервые изложены в докладе Эмилия Розенова и позднее развиты
в его статье «Закон золотого сечения в поэзии и музыке». Розенов показал действие данной пропорции в музыкальных формах эпохи Барокко и классицизма на примере произведений Баха, Моцарта, Бетховена.
Золотое сечение в музыке
Слайд 77
Золотое сечение в поэзии
Примеры из поэзии бесчисленны. Исследователи
особенно выделяют гений А.С. Пушкина.
Наиболее часто в стихотворениях А.С.
Пушкина встречающиеся размеры его стихов тяготеют к числам 5, 8, 13, 21, 34, размер близок к числам ряда Фибоначчи. На эти строки приходятся смысловые максимумы стихотворений.
Слайд 78
"Не дорого ценю я громкие права..."
Не дорого ценю

я громкие права,
От коих не одна кружится голова.
Я не
ропщу о том, что отказали боги
Мне в сладкой участи оспаривать налоги
Или мешать царям друг с другом воевать;
И мало горя мне, свободно ли печать
Морочит олухов, иль чуткая цензура
В журнальных замыслах стесняет балагура.
Все это, видите ль, слова, слова, слова.
Иные, лучшие, мне дороги права:
Иная, лучшая, потребна мне свобода:
Зависеть от царя, зависеть от народа -
Не все ли нам равно? Бог с ними.
Никому отчета не давать, себе лишь самому
Служить и угождать; для власти, для ливреи
Не гнуть ни совести, ни помыслов, ни шеи;
По прихоти своей скитаться здесь и там,
Дивясь божественным природы красотам,
И пред созданьями искусств и вдохновенья
Трепеща радостно в восторгах умиленья,
Вот счастье! Вот права ...
21 строка.
Две смысловые части: в 13 и 8 строк.
Первая часть этого стиха по смысловому содержанию делится на 8 и 5 строк.
Все стихотворение построено по законам золотой пропорции.
Слайд 79
Пора, мой друг, пора!
Пора, мой друг, пора! Покоя сердце просит –
Летят
за днями дни, и каждый час уносит
Частичку бытия, а
мы с тобой вдвоем
Предполагаем жить… И глядь – как раз – умрем.
На свете счастья нет, но есть покой и воля.
Давно завидная мечтается мне доля –
Давно, усталый раб, замыслил я побег
В обитель дальнюю трудов и чистых нег.
8 строк.
Две смысловые части.
1 часть -5 строк.
2 часть – 3 строки.
Это закономерность творческого восприятия поэта, интуитивное чувство гармонии.