Презентация на тему Перпендикулярные прямые в пространстве

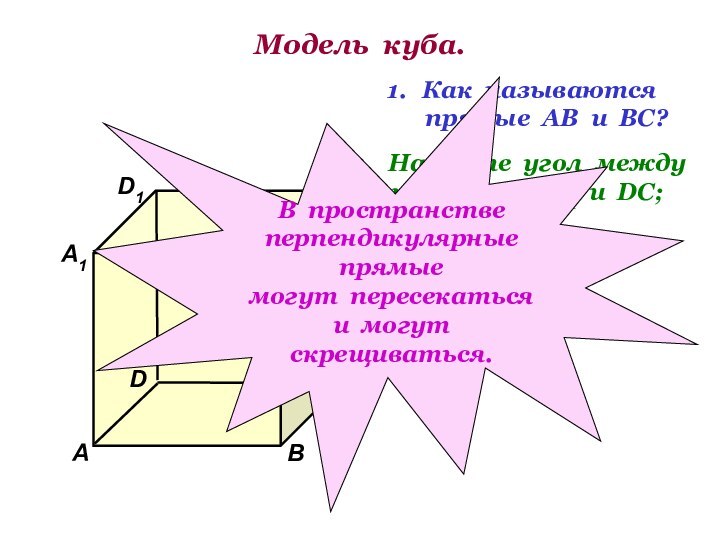
и ВС?
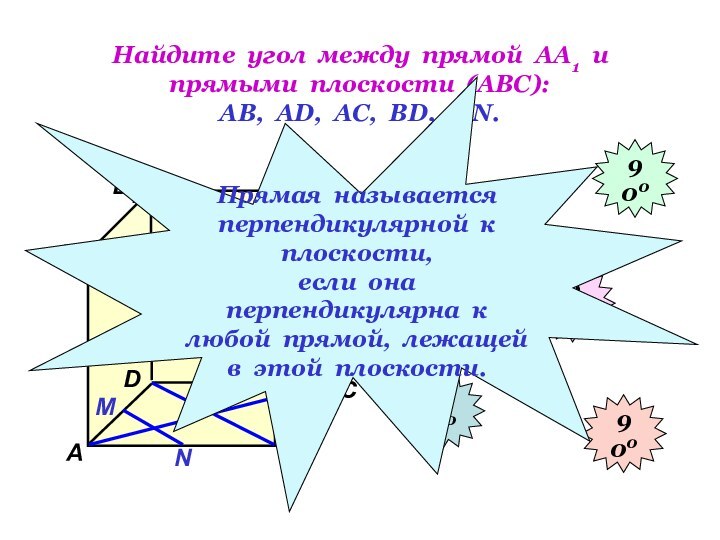
Найдите угол между
прямыми АА1 и

DC;
ВВ1 и АD.

В пространстве
перпендикулярные прямые
могут пересекаться
и могут скрещиваться.

СС1 ; DC СС1

АА1

DC

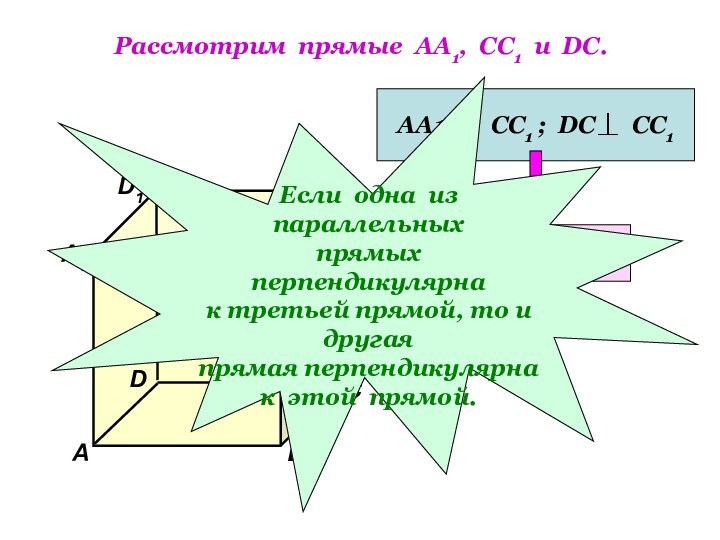
Если одна из параллельных
прямых перпендикулярна
к третьей прямой, то и другая
прямая перпендикулярна
к этой прямой.

этой прямой, то и другая прямая перпендикулярна к этой

прямой

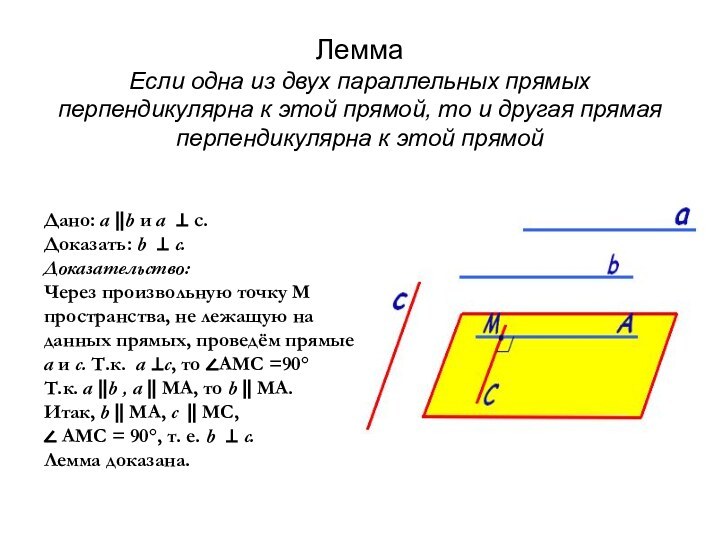
Дано: а ⃦b и а ⊥ с. Доказать: b ⊥ c.
Доказательство: Через произвольную точку М пространства, не лежащую на данных прямых, проведём прямые а и с. Т.к. а ⊥с, то ∠АМС =90° Т.к. а ⃦b , а ⃦ МА, то b ⃦ МА. Итак, b ⃦ МА, с ⃦ МС,
∠ АМС = 90°, т. е. b ⊥ c. Лемма доказана.

(АВС): АВ, АD, АС, ВD, МN.
D1
В
А1
А




D
С1
С
В1



N
М
900
900
900
900
900
Прямая называется
перпендикулярной к плоскости,
если она

перпендикулярна к
любой прямой, лежащей
в этой плоскости.

прямых перпендикулярна

плоскости, то и другая прямая перпендикулярна к этой плоскости.

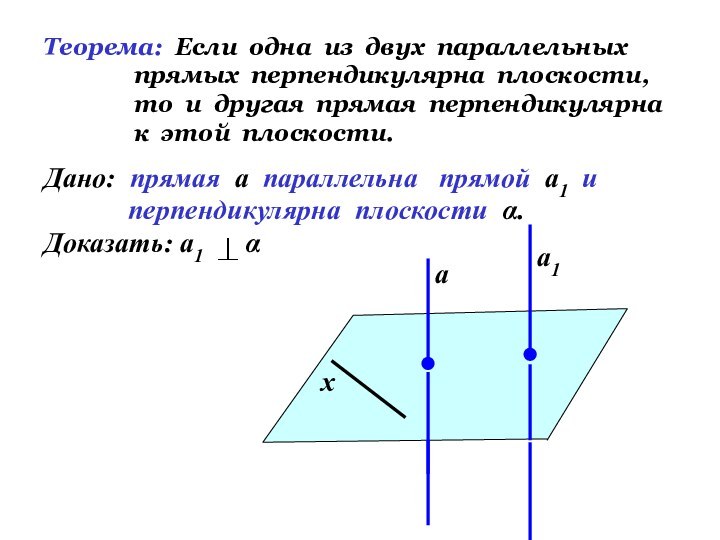
Дано: прямая а параллельна прямой а1 и
перпендикулярна плоскости α.
Доказать: а1 α

а

а1

х

к плоскости, то и другая прямая перпендикулярна к этой

плоскости.

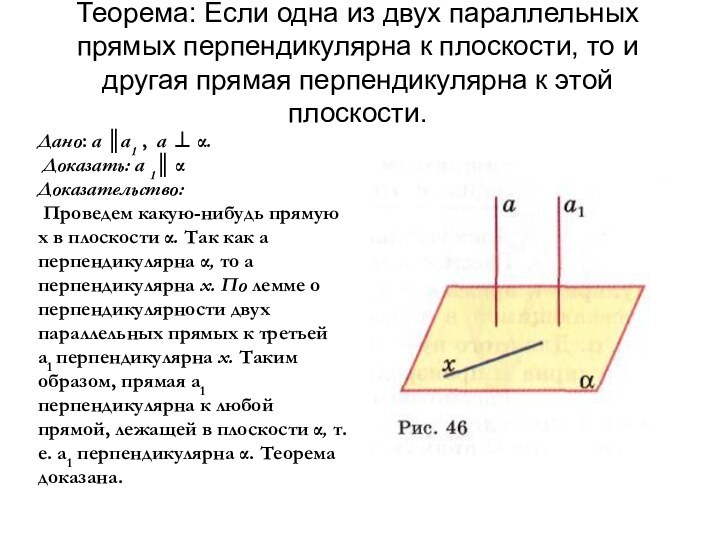
Дано: а ║а1 , а ⊥ α.
Доказать: а 1║ α
Доказательство: Проведем какую-нибудь прямую х в плоскости α. Так как а перпендикулярна α, то а перпендикулярна х. По лемме о перпендикулярности двух параллельных прямых к третьей а1 перпендикулярна х. Таким образом, прямая а1 перпендикулярна к любой прямой, лежащей в плоскости α, т.е. а1 перпендикулярна α. Теорема доказана.
 

Если две прямые перпендикулярны к

плоскости, то они параллельны.

M

c

они параллельны.

Дано: a ⊥α,b ⊥α (а)
Доказать : a ║

b .
Доказательство:
Через какую-нибудь точку M прямой b проведем прямую b1, параллельную прямой a. По предыдущей теореме b1 ⊥α. Докажем ,что прямая b1 совпадает с прямой b .Тем самым будет доказано ,что a ║ b .Допустим ,что прямые b и b1 не совпадают .Тогда в плоскости β,содержащей прямые b и b1, через точку М проходят две прямые, перпендикулярные к прямой c ,по которой пересекаются плоскости α и β (б).Но это невозможно, следовательно, a║b. Теорема доказана.