существовании обитателей Марса подобных человеку, это явилось следствием открытий
итальянского астронома Скиапарелли (открыл на Марсе каналы которые долгое время считались искусственными) и др.Удивительно!
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть









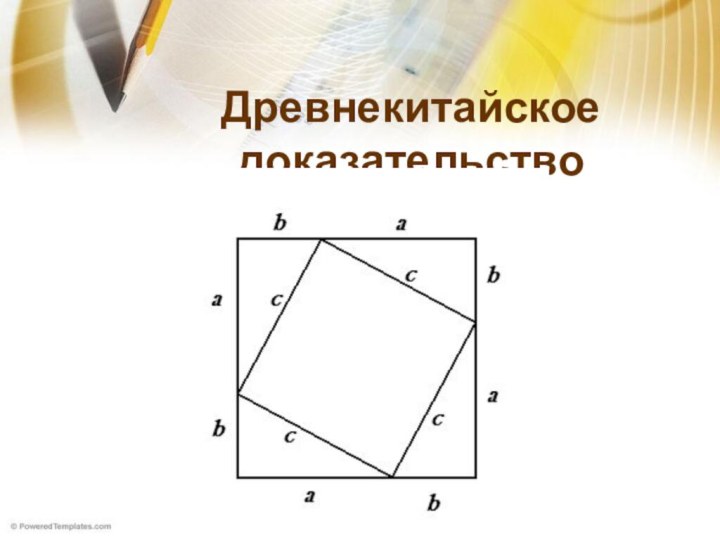
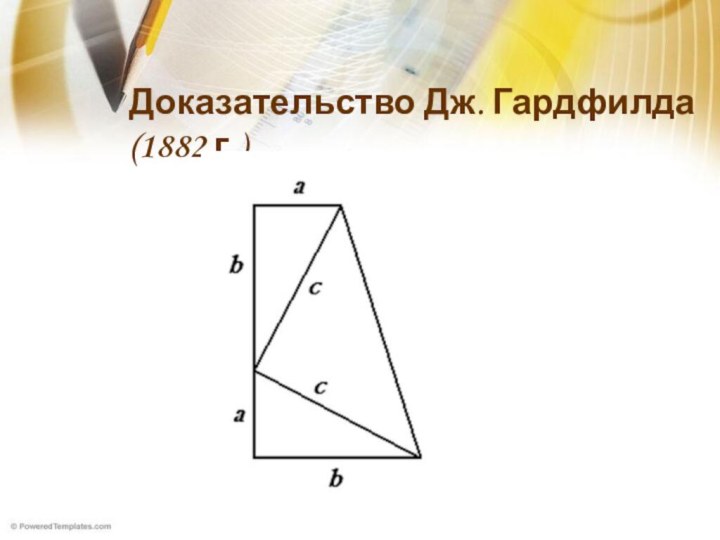
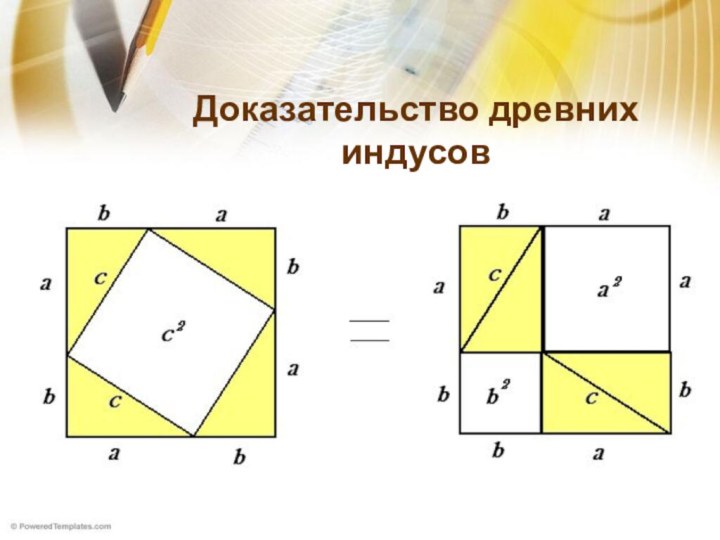
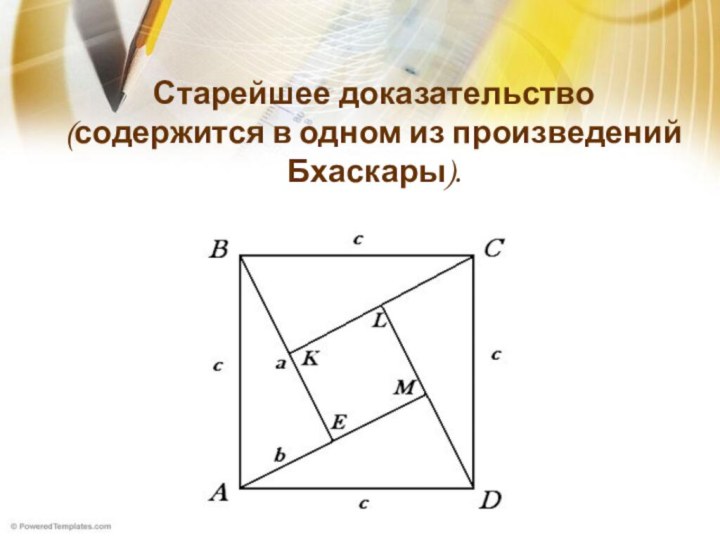
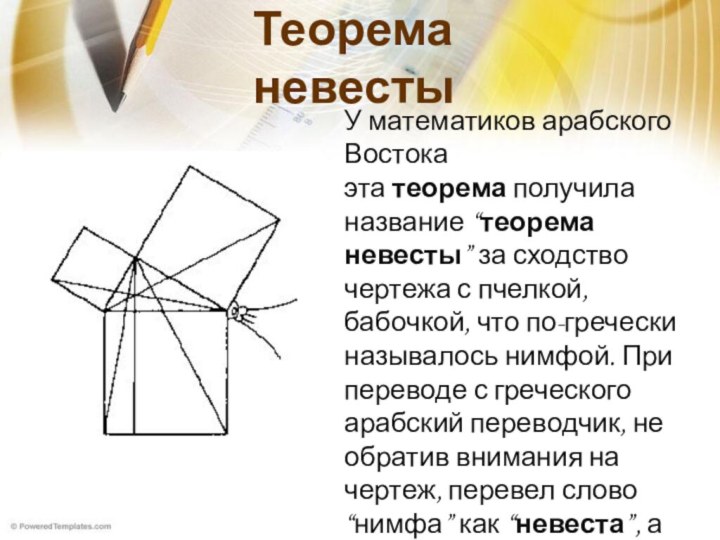

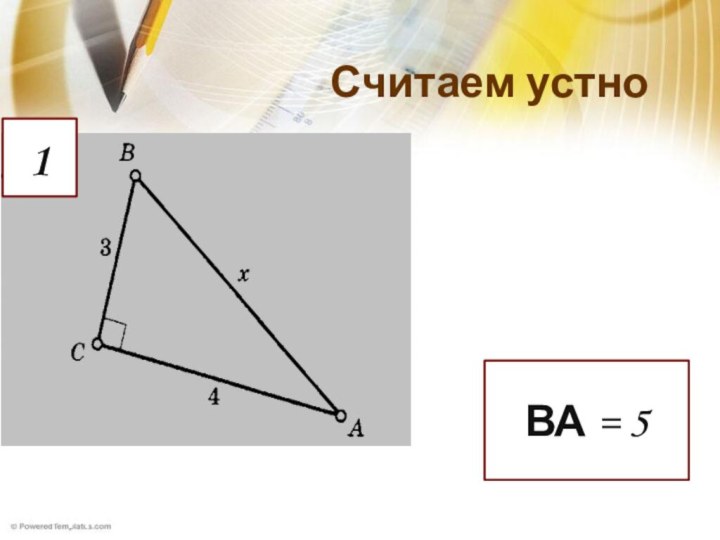
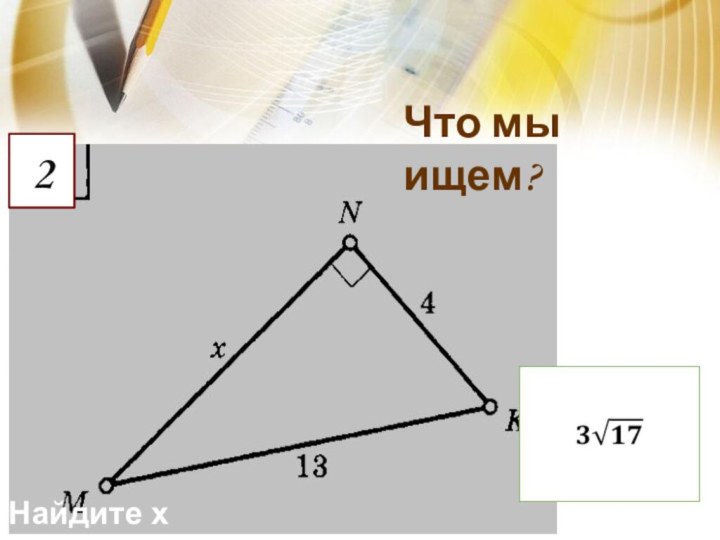
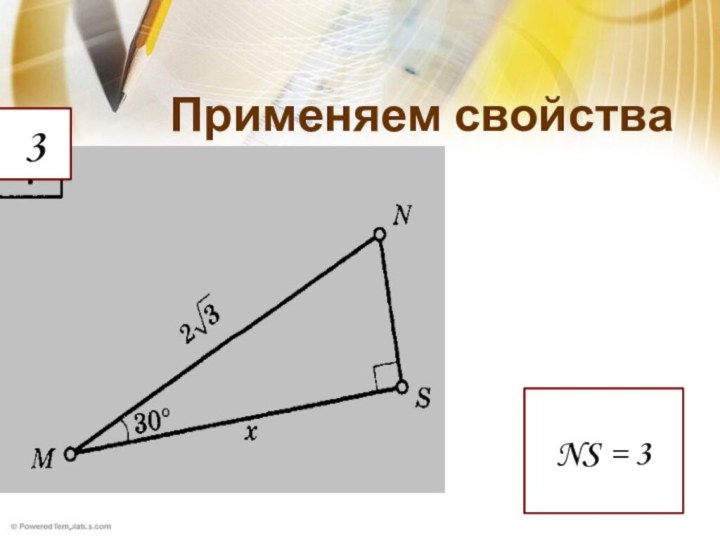
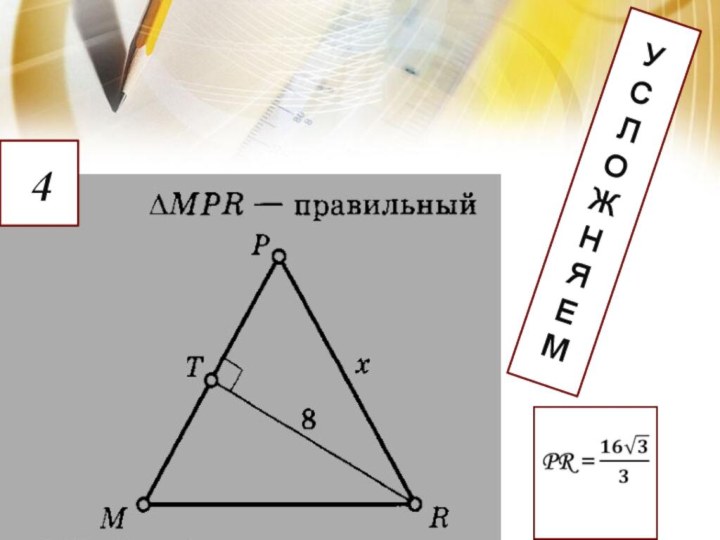
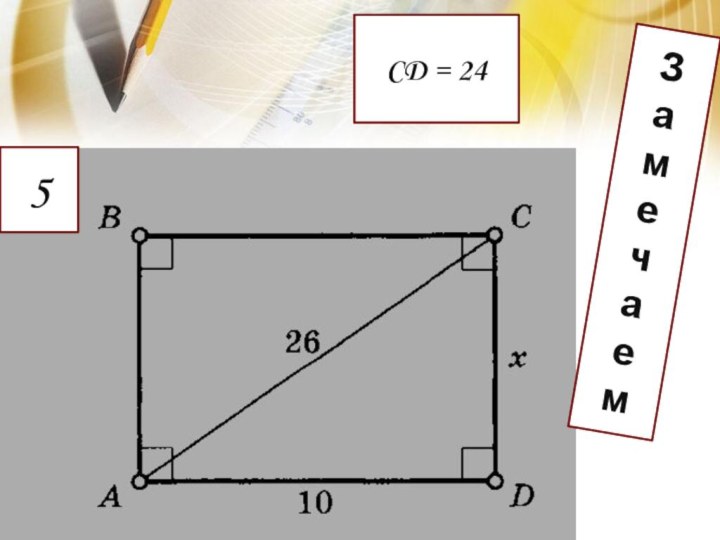
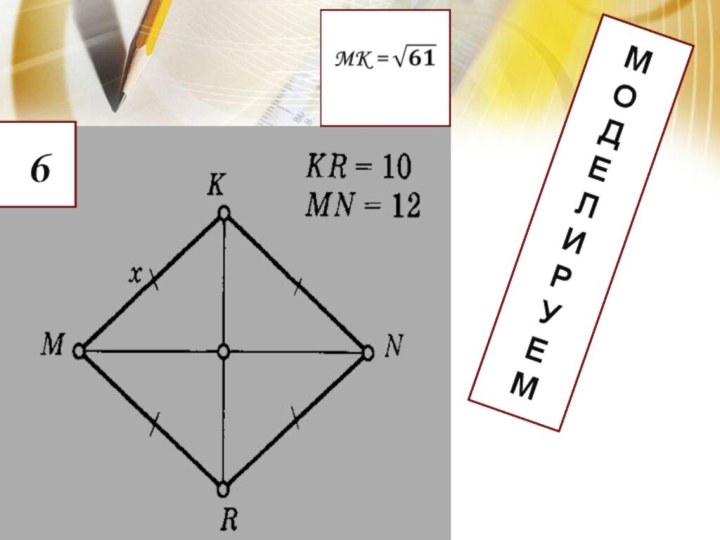
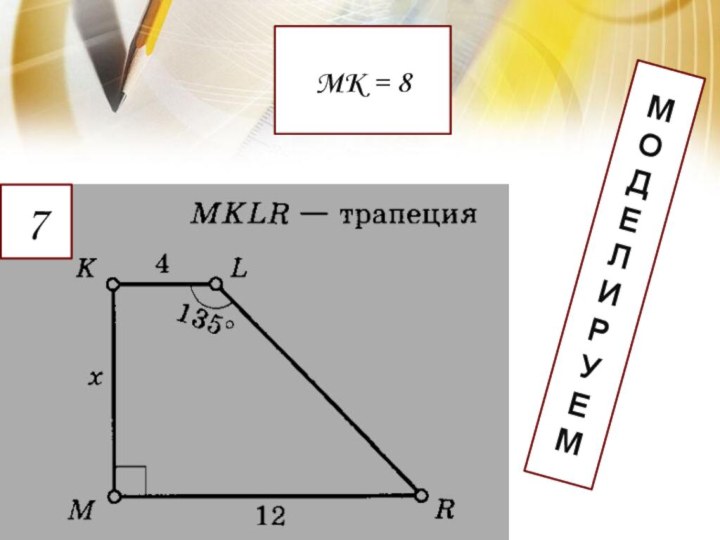






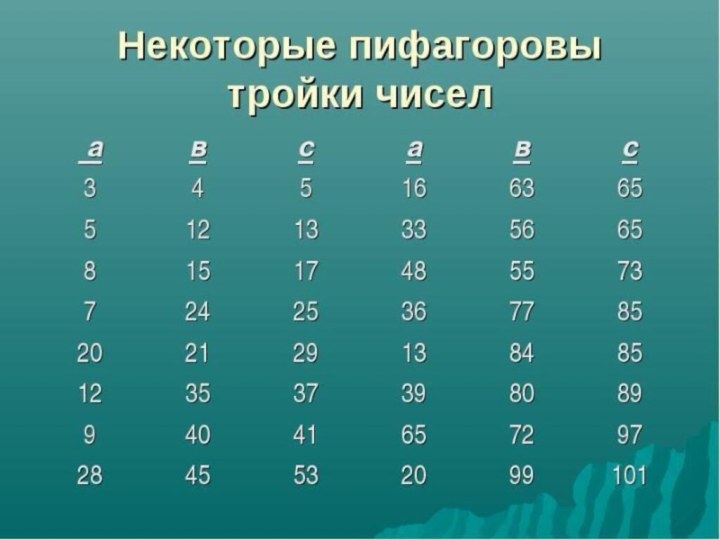
Удивительно!