Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по геометрии на тему Параллельность прямых (10 класс)

Содержание

Структура урокаПараллельные прямые в пространстве.Параллельность трех прямых.Параллельность прямой и плоскости.Параллельность плоскостей.Свойства параллельных плоскостей.
Геометрия, 10 классПараллельность прямых в пространстве Структура урокаПараллельные прямые в пространстве.Параллельность трех прямых.Параллельность прямой и плоскости.Параллельность плоскостей.Свойства параллельных плоскостей. Параллельные прямые в пространстве Определение Две прямые в пространстве называются параллельными, ОпределениеДве прямые называются скрещивающимися, если они не лежат в одной плоскости.Прямые a и d ТеоремаЧерез любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная Параллельность отрезков, отрезка и прямой, лучей.Два отрезка называются параллельными, если они лежат ЛеммаЕсли одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость. Параллельность трех прямых Теорема Если две Параллельность прямой и плоскостиВозможны три случая взаимного расположения прямой и плоскости в ТеоремаЕсли прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в Следствие Если плоскость проходит через данную прямую параллельную другой плоскости, и пересекает СледствиеЕсли одна из двух параллельных прямых параллельна данной плоскости, то другая прямая 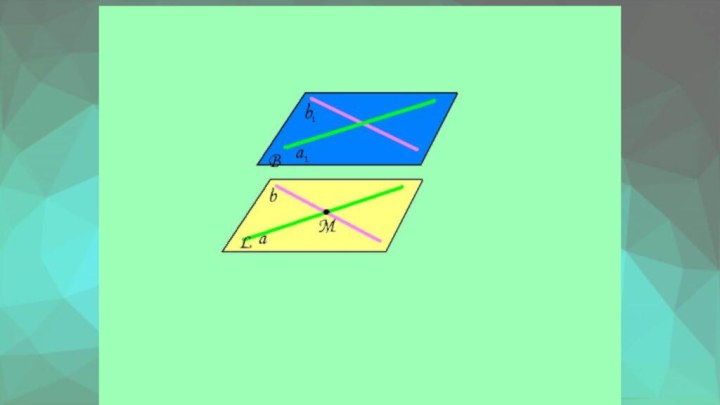Параллельность плоскостейОпределениеДве плоскости называются параллельными, если они не пересекаются. 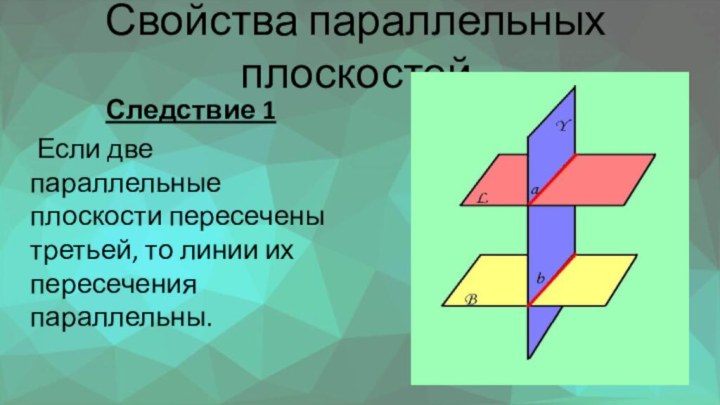Теорема Если две Свойства параллельных плоскостейСледствие 1 Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Свойства параллельных плоскостейСледствие 2Отрезки параллельных прямых, заключенных между параллельными плоскостями равны.
Слайды презентации

Слайд 2 Структура урока
Параллельные прямые в пространстве.
Параллельность трех прямых.
Параллельность прямой

Структура урокаПараллельные прямые в пространстве.Параллельность трех прямых.Параллельность прямой и плоскости.Параллельность плоскостей.Свойства параллельных плоскостей.

и плоскости.
Параллельность плоскостей.
Свойства параллельных плоскостей.

Слайд 3 Параллельные прямые в пространстве
Определение
Две прямые

Параллельные прямые в пространстве Определение Две прямые в пространстве называются параллельными,

в пространстве называются параллельными, если они лежат в одной

плоскости и не пересекаются.

Обозначение а ιι b с ιι d

/

Слайд 4 Определение
Две прямые называются скрещивающимися, если они не лежат

ОпределениеДве прямые называются скрещивающимися, если они не лежат в одной плоскости.Прямые a и d

в одной плоскости.
Прямые a и d

Слайд 5 Теорема
Через любую точку пространства, не лежащую на данной

ТеоремаЧерез любую точку пространства, не лежащую на данной прямой, проходит прямая,

прямой, проходит прямая, параллельная данной, и причем только одна

Слайд 6 Параллельность отрезков, отрезка и прямой, лучей.
Два отрезка называются

Параллельность отрезков, отрезка и прямой, лучей.Два отрезка называются параллельными, если они

параллельными, если они лежат на параллельных прямых.
Отрезок и прямая

называются параллельными, если они лежат на параллельных прямых.
Два луча называются параллельными, если они лежат на параллельных прямых.

Слайд 7 Лемма
Если одна из двух параллельных прямых пересекает данную

ЛеммаЕсли одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

плоскость, то и другая прямая пересекает эту плоскость.

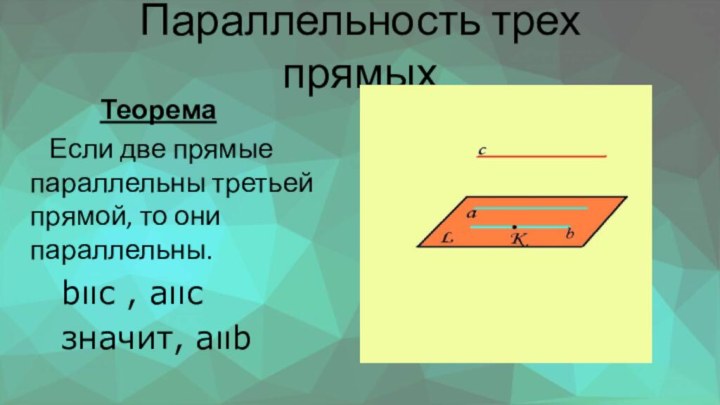
Слайд 8 Параллельность трех прямых

Параллельность трех прямых Теорема Если две прямые параллельны третьей

Теорема
Если две прямые параллельны третьей прямой, то

они параллельны.

bιιс , аιιс
значит, аιιb

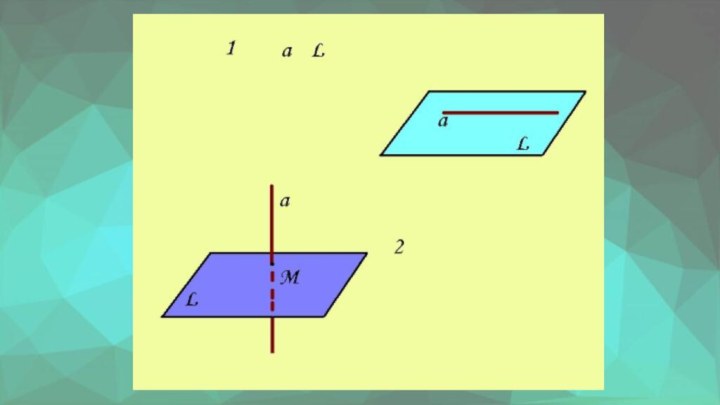
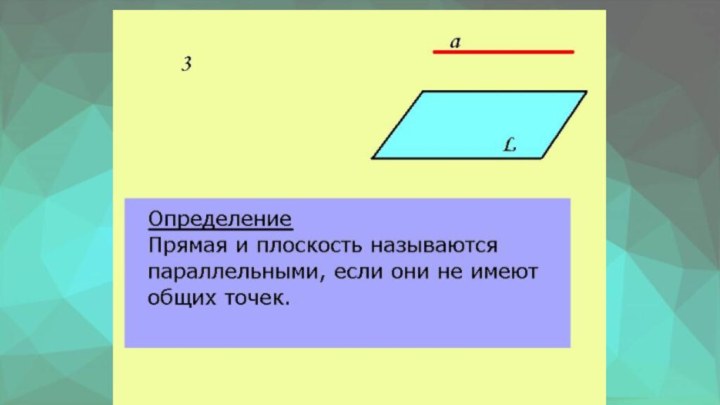
Слайд 9 Параллельность прямой и плоскости
Возможны три случая взаимного расположения

Параллельность прямой и плоскостиВозможны три случая взаимного расположения прямой и плоскости

прямой и плоскости в пространстве:

Прямая лежит в плоскости.
Прямая и

плоскость имеют только одну точку.
Прямая и плоскость не имеют общих точек.

Слайд 10

Слайд 11

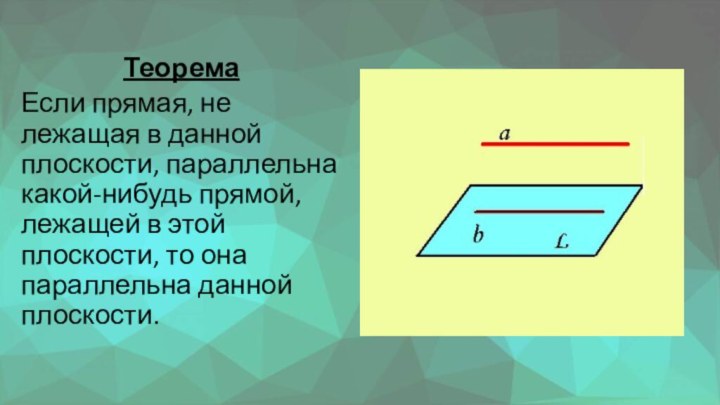
Слайд 12 Теорема
Если прямая, не лежащая в данной плоскости, параллельна

ТеоремаЕсли прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей

какой-нибудь прямой, лежащей в этой плоскости, то она параллельна

данной плоскости.

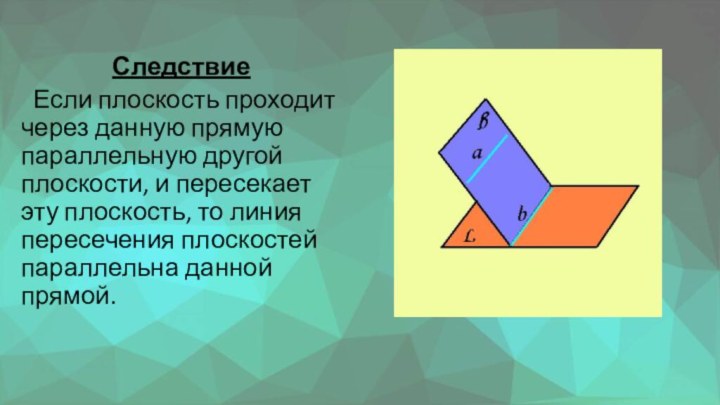
Слайд 13 Следствие
Если плоскость проходит через данную прямую параллельную

Следствие Если плоскость проходит через данную прямую параллельную другой плоскости, и

другой плоскости, и пересекает эту плоскость, то линия пересечения

плоскостей параллельна данной прямой.

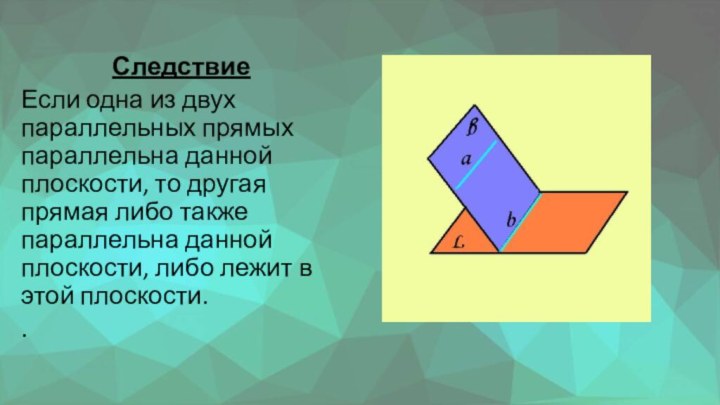
Слайд 14 Следствие
Если одна из двух параллельных прямых параллельна данной

СледствиеЕсли одна из двух параллельных прямых параллельна данной плоскости, то другая

плоскости, то другая прямая либо также параллельна данной плоскости,

либо лежит в этой плоскости.
.

Слайд 15 Параллельность плоскостей
Определение
Две плоскости называются параллельными, если они не

Параллельность плоскостейОпределениеДве плоскости называются параллельными, если они не пересекаются. Теорема Если

пересекаются.
Теорема
Если две пересекающиеся прямые одной плоскости соответственно параллельны

двум пересекающимся прямым другой плоскости, то эти плоскости параллельны

Слайд 16

Слайд 17 Свойства параллельных плоскостей
Следствие 1
Если две параллельные плоскости

Свойства параллельных плоскостейСледствие 1 Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

пересечены третьей, то линии их пересечения параллельны.

  • Имя файла: prezentatsiya-po-geometrii-na-temu-parallelnost-pryamyh-10-klass.pptx
  • Количество просмотров: 203
  • Количество скачиваний: 1
- Предыдущая Презентация по русскому языку Праздник Букваря
Следующая - Презентация по биологии Великие анатомы

Похожие презентации

Пифагор и его теорема Пифагор и его теорема 157
Векторлардың скаляр көбейтіндісі 9 сынып Векторлардың скаляр көбейтіндісі 9 сынып 281
Векторы в пространстве Векторы в пространстве 141
Тригонометрические формулы Тригонометрические формулы 176
Интересные факты о теореме Пифагора Интересные факты о теореме Пифагора 203
Презентация по математике на тему Преобразования в геометрии и не только Презентация по математике на тему Преобразования в геометрии и не только 154
Координатный метод в пространстве Координатный метод в пространстве 189
Тетраэдр и Параллелепипед Тетраэдр и Параллелепипед 171
Презентация по геометрии на тему Призма (11 класс) Презентация по геометрии на тему Призма (11 класс) 172
Разработка урока по теме Теорема Пифагора Разработка урока по теме Теорема Пифагора 149
Музей истории четырёхугольников Музей истории четырёхугольников 217
Построение сечений тетраэдра и параллелепипеда Построение сечений тетраэдра и параллелепипеда 303
Синус и косинус острого угла Синус и косинус острого угла 237
Геометрические фигуры 4 класс Геометрические фигуры 4 класс 198
Презентация по математике на тему Объём цилиндра Презентация по математике на тему Объём цилиндра 194
Подобие правильных многоугольников Подобие правильных многоугольников 188
Методическая разработка по теме Определение параллелограмма. Свойства параллелограмма Методическая разработка по теме Определение параллелограмма. Свойства параллелограмма 177
Презентация задач по теореме Пифагора Презентация задач по теореме Пифагора 147
Линейная функция и ее график Линейная функция и ее график 152
Коллинеарные и компланарные векторы Коллинеарные и компланарные векторы 172
Презентация по теме: Осевая симметрия Презентация по теме: Осевая симметрия 147
Платоновы тела как основа мироздания Платоновы тела как основа мироздания 168
Решение задач по теме Теорема Пифагора Решение задач по теме Теорема Пифагора 171
Презентация по геометрии Трапеция (8 класс) Презентация по геометрии Трапеция (8 класс) 148
Осевая и центральная симметрии Осевая и центральная симметрии 164
Математикадан презентация:Шар тақырыбы бойынша ұлттық бірыңғай тестке дайындық(11 сынып) Математикадан презентация:Шар тақырыбы бойынша ұлттық бірыңғай тестке дайындық(11 сынып) 202
Презентация по геометрии Решение задач на применение третьего признака равенства треугольников (7 класс) Презентация по геометрии Решение задач на применение третьего признака равенства треугольников (7 класс) 136
Презентация по геометрии на тему Смежные и вертикальные углы (7 класс) Презентация по геометрии на тему Смежные и вертикальные углы (7 класс) 150
Презентация по математике на тему Соотношения между сторонами и углами треугольника 7 класс Презентация по математике на тему Соотношения между сторонами и углами треугольника 7 класс 192
Презентация по геометрии на тему: Признаки равенства треугольников (7 класс) Презентация по геометрии на тему: Признаки равенства треугольников (7 класс) 146