- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Осевая симметрия. полезные материалы для учителя
Содержание
- 2. Свойства осевой симметрии.Осевая симметрия пространства есть движение,
- 3. При осевой симметрии: --- неподвижной
- 4. Осевая симметрия- симметрия относительно прямой. чтобы
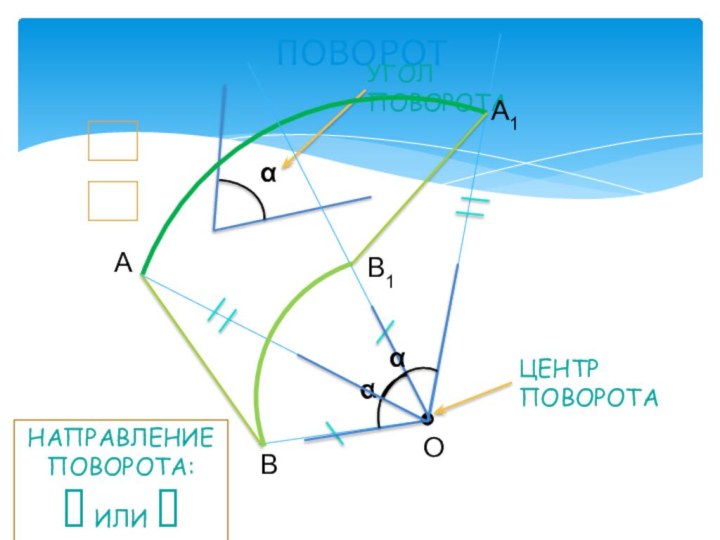
- 5. ПОВОРОТОАВА1В1НАПРАВЛЕНИЕ ПОВОРОТА: ИЛИ
- 6. ПОВОРОТ - движение, при котором по крайней
- 7. Параллельным переносом называют преобразование плоскости, при
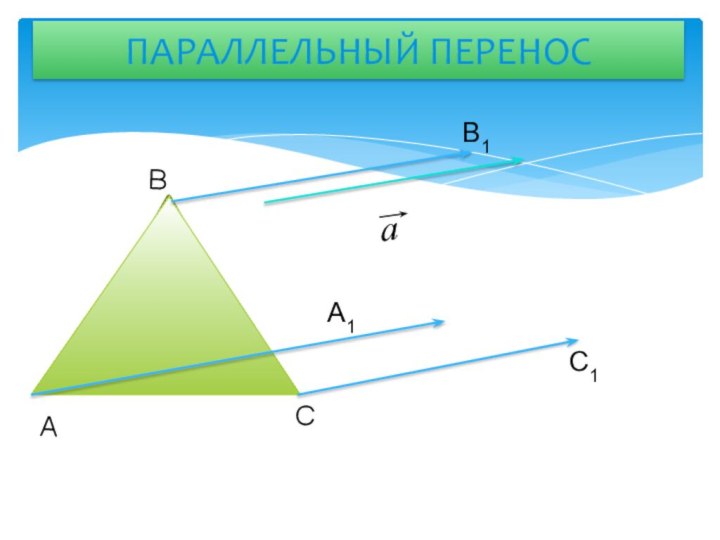
- 8. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОСС1А1В1САВ
- 9. Свойства параллельного переноса.У параллельного переноса нет неподвижных точек.Параллельным
- 10. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС Сделаем вывод:Чтобы отобразить фигуру с
- 11. Любая фигура переходит в равную ей
- 12. Рассмотренные отображения плоскости на себя:симметрия относительно прямойасимметрия
- 13. Скачать презентацию
- 14. Похожие презентации
Свойства осевой симметрии.Осевая симметрия пространства есть движение, а значит, обладает всеми свойствами движений: переводит прямую в прямую, отрезок ---в отрезок, луч ---в луч, плоскость ---в плоскость. Кроме того, это преобразование пространства, совпадающее со своим
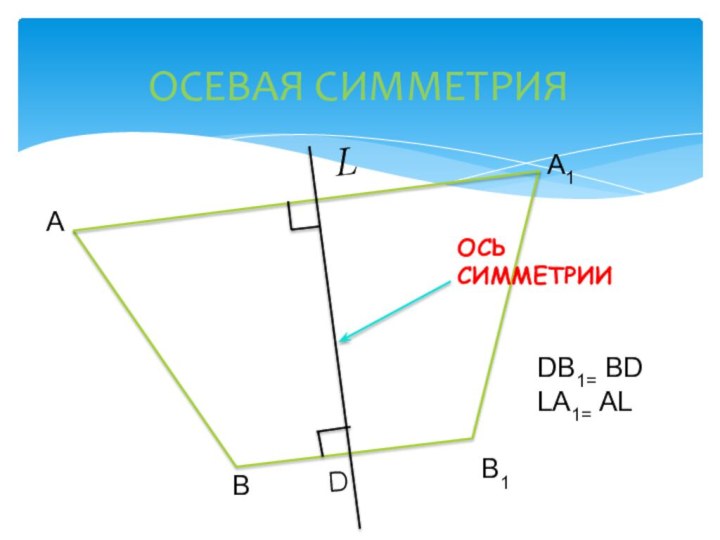










Слайд 3 При осевой симметрии: --- неподвижной является каждая точка
оси симметрии и других неподвижных точек не существует; ---
неподвижной прямой является ось симметрии (на ней индуцируется тождественное преобразование) и любая прямая, пересекающая ось симметрии и ей перпендикулярная (на каждой из этих прямых индуцируется центральная симметрия относительно точки ее пересечения с осью симметрии) ; --- неподвижной является любая плоскость, перпендикулярная оси (в каждой такой плоскости индуцируется центральная симметрия относительно точки ее пересечения с осью симметрии) ; При осевой симметрии:Слайд 4 Осевая симметрия- симметрия относительно прямой. чтобы построить фигуру,
симметричную данной относительно прямой LD, нужно: 1) из каждой точки
фигуры провести перпендикуляр к прямой LD. 2) продолжить полученный отрезок равным ему, 3) отметить на конце этого отрезка образ исходной точки, затем соединить полученные образы. FINISHСлайд 6 ПОВОРОТ - движение, при котором по крайней мере
одна точка плоскости (пространства) остаётся неподвижной.
Чтобы получить отображение фигуры при повороте
около данной точки, нужно:каждую точку фигуры повернуть на один и тот же угол в одном и том же направлении (по часовой стрелке или против часовой стрелки)
P.s. при движении угол переходит в равный ему угол.
Слайд 7 Параллельным переносом называют преобразование плоскости, при котором все
точки смещаются по параллельным прямым на одно и то
же расстояниеА
В
А1
В1
Слайд 9
Свойства параллельного переноса.
У параллельного переноса нет неподвижных точек.
Параллельным переносом на
некоторый заданный вектор называется такое отображение плоскости на саму себя,
при котором каждая точка А плоскости переходит в такую точку А1 той же плоскости, чтобы АА1= аЗначит, расстояние между векторами и точками равно.
Таким образом, параллельный перенос сохраняет расстояние между точками и поэтому представляет собой движение.
Параллельный перенос перемещает каждую точку фигуры или пространства на одно и то же расстояние в одном и том же направлении.
При параллельном переносе прямая переходит либо в себя, либо в параллельную ей прямую.
Параллельный перенос задается парой соответствующих точек, т.е. каковы бы ни были точки, существует единственный параллельный перенос, при котором точка переходит в точку.
Слайд 10
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
Сделаем вывод:
Чтобы отобразить фигуру с помощью параллельного
переноса, нужно:
каждую точку фигуры переместить на заданный вектор
соединить
полученные образы
Слайд 11
Любая фигура переходит
в равную ей фигуру
Фигуры называются равными,
если существует движение , отображающее одну из них на другую.
Внимание!
Слайд 12
Рассмотренные отображения плоскости на себя:
симметрия относительно
прямой
а
симметрия относительно
точки
О
параллельный
перенос
на вектор а
поворот
вокруг точки О на угол а
О
являются движениями.
а
а