Слайд 2
Цель и задачи
Цель: Изучить основы расчета кредитов, для
дальнейшего применения их в различных жизненных ситуациях связанных с
выбором типа кредита и для решения экзаменационных задач.
Задачи:
Провести анализ учебной и специализированной литературы.
Изучить математические основы кредитования и выявить возможности использования математических знаний для решения практических задач.
Провести статистический анализ полученных результатов.
Слайд 3
Определение кредита
Кредит – предоставление банком или кредитной организацией денег
заемщику в размере и на условиях, предусмотренных кредитным договором,
по которому заемщик обязан возвратить полученную сумму и уплатить проценты по ней.
Слайд 4
Кредитный договор
В договоре о кредите прописываются следующие условия:
срок
действия кредитования. Обязательно называется период, за который клиент гарантирует
выплату всей суммы долга, а также проценты по взятому займу;
размер основного долга;
в каком размере должны быть выплачены ежемесячные платежи;
установленная процентная ставка по данному кредиту;
при наличии залога информация о нем.
Слайд 5
История появления
История кредита начинается с древнейших времен. Считается,
что кредитование уже существовало в Ассирии, Вавилоне и Древнем
Египте.
В Древней Греции основными кредиторами выступали храмы, которые служили первыми резервными фондами - на время неурожая.
В современном понимании история кредитования ведет свое начало со времен промышленной революции. А наибольшего развития кредитование достигло лишь после отмены крепостного права и позднее во время промышленной революции.
Слайд 6
Виды кредитов
Автокредит
Ипотечное кредитование
Ломбард
Заем
Потребительский кредит
Слайд 7
Формулы расчета
Существует несколько методов расчета процентов по кредиту,
а именно:
Ежемесячный возврат части кредита с уплатой процентов (дифференцированный
метод).
Аннуитетный платеж.
Слайд 8
Дифференцированный метод
b = S / N
b – основной
платёж, S – размер кредита, N – количество месяцев.
Sn
= S — (b * n)
n – количество прошедших периодов.
p= Sn * P / 12/100
p – начисленные проценты, Sn — остаток задолженности на период, P – годовая процентная ставка по кредитy.
Слайд 9
Дифференцированный метод
S – размер кредита – 1000,00 ед.
N
– количество месяцев – 12 мес.
P - Процентная ставка
кредита “годовых” – 20 %
Слайд 11
Аннуитетный платеж
A = K · S
Где А —
ежемесячный аннуитетный платёж, К — коэффициент аннуитета, S —
сумма кредита.
где i — месячная процентная ставка по кредиту (= годовая ставка / 12),
n — количество периодов, в течение которых выплачивается кредит.
Поскольку периодичность платежей по кредиту — ежемесячно, то ставка по кредиту (i) берётся месячная. Если процентная ставка 12% годовых, то месячная ставка:
i = 12% / 12 мес = 1%.
Слайд 12
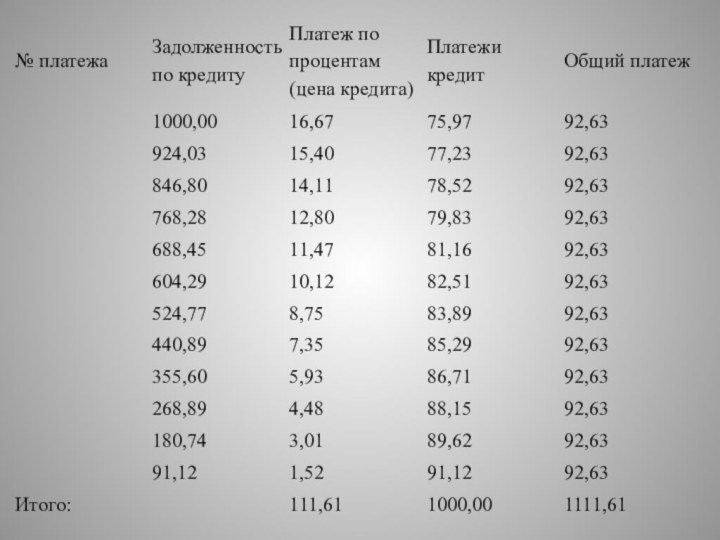
Аннуитетный платеж
S – размер кредита – 1000,00 ед.
N
– количество месяцев – 12 мес.
P - Процентная ставка
кредита “годовых” – 20 %
Слайд 14
Практическая работа
№1 Опрос учителей
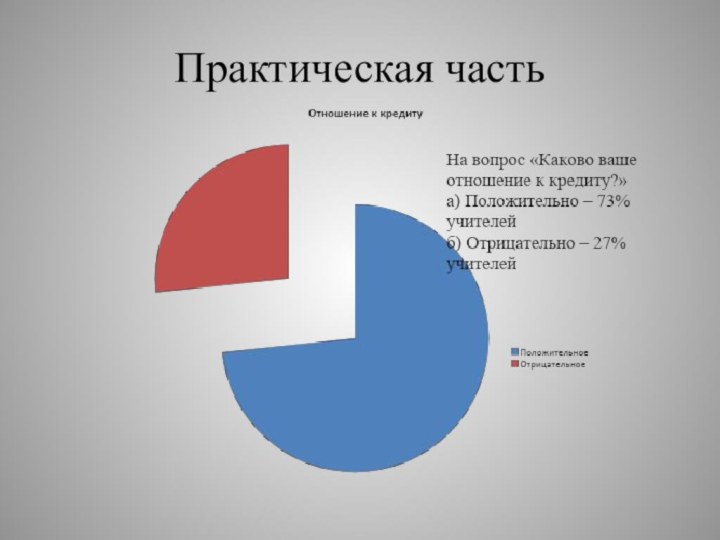
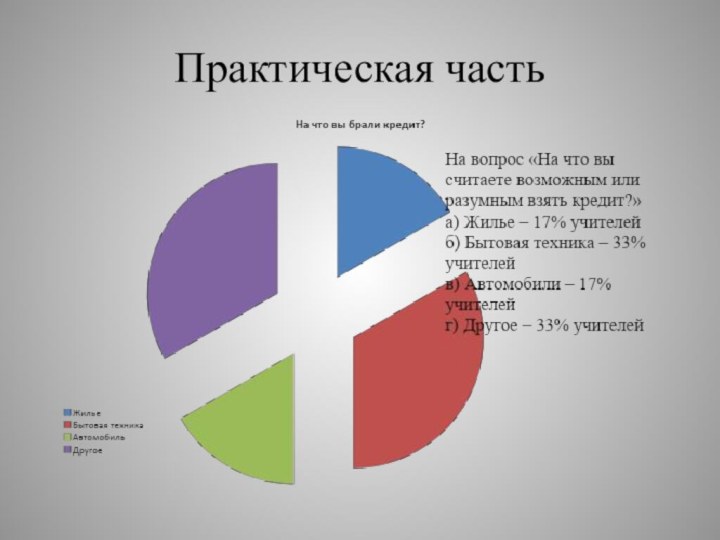
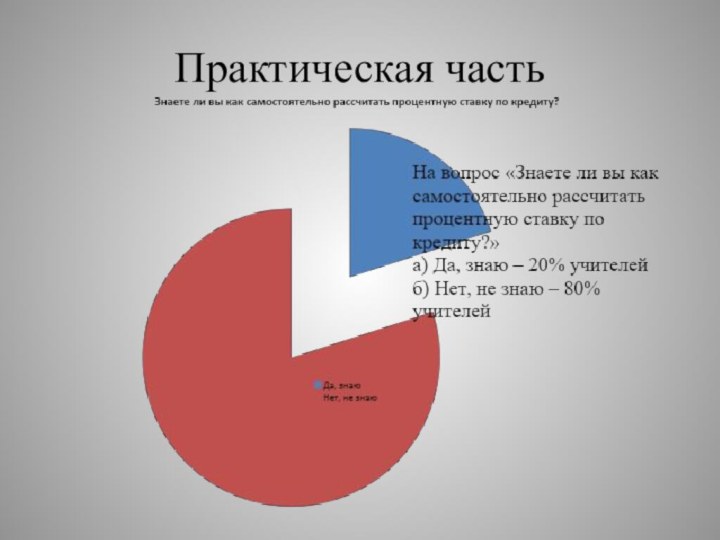
Цель: Определить отношение людей к
кредитам.
Задачи:
Сделать опрос среди учителей школы.
Изучить отношение учителей к
кредитам.
Подвести итоги.
Слайд 19
Практическая часть
№2 Решение задач
Если я хочу взять
кредит на учебу.
Я иду в банк и беру
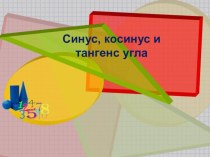
кредит на 1 год на сумму 200 000 рублей под 15 процентов годовых (месячная процентная ставка – 1,25%). Кредит погашается ежемесячно: с 15.07.2019 по 15.06.2020.
Слайд 20
Расчет платежей по кредиту при дифференцированном методе
Практическая часть
Слайд 21
Практическая часть
Расчет платежей по кредиту при аннуитетном
методе.
Слайд 22
Практическая часть
Также можно решить задачу из ЕГЭ
под №17.
Родион хочет взять кредит на некоторую сумму и
выбирает между двумя банками. Первый банк предлагает кредит на 15 лет под 6% годовых, второй – на 6 лет под 14% годовых, причем в обоих банках дифференцированная система платежей. Определите, в какой банк выгоднее обратиться Родиону и сколько процентов от кредита составляет эта выгода.