- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии Площадь трапеции (8 класс)
Содержание
- 2. Цели урока:- познакомиться с формулой вычисления площади трапеции, - повторить и закрепить знания по теме «Площади».
- 3. Вопросы (устно): Какую тему мы сейчас изучаем?Площади,
- 4. Задачи по изученному материалу№ 1. Площадь прямоугольника
- 5. Тест1. Равные … имеют … площади.2. Площадь
- 6. Высота трапеции равна меньшему основанию
- 7. Площадь трапецииТема урока
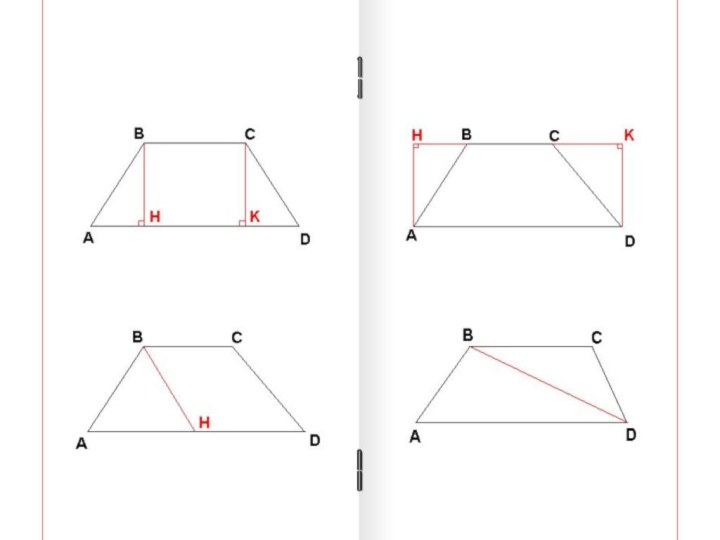
- 8. «Открытие» нового знания. Дана трапеция АВСД с
- 10. Формула площади трапеции
- 11. Скачать презентацию
- 12. Похожие презентации
Цели урока:- познакомиться с формулой вычисления площади трапеции, - повторить и закрепить знания по теме «Площади».
Слайд 2
Цели урока:
- познакомиться с формулой вычисления площади трапеции,
- повторить и закрепить знания по теме «Площади».
Слайд 3
Вопросы (устно):
Какую тему мы сейчас изучаем?
Площади, каких фигур
мы уже знаем?
Какой прием используется при выводе формул площадей?
Слайд 4
Задачи по изученному материалу
№ 1. Площадь прямоугольника равна
75см2 . Найдите стороны этого прямоугольника, если одна из
них в три раза больше другой.№ 2. Сторона параллелограмма 6 см, а диагональ, равная 10 см, образует с ней угол 30. Найдите площадь параллелограмма.
Слайд 5
Тест
1. Равные … имеют … площади.
2. Площадь …
равна квадрату … .
3. Если … составлен из …
многоугольников, то его … равна … площадей этих многоугольников.4. Площадь прямоугольника равна … его смежных … .
5. Высотой параллелограмма называется …, проведенный из любой … противоположной стороны к …, содержащей основание.
6. Площадь … равна произведению его … на … .
7. Площадь треугольника … половине … его … на … .
8. Площадь … треугольника равна половине … его катетов.
9. Площадь ромба равна … произведению его … .
Слайд 6 Высота трапеции равна меньшему основанию и
в два раза меньше большего основания. Найти высоту трапеции,
если ее площадь равна 54см2.
Слайд 8
«Открытие» нового знания.
Дана трапеция АВСД с основаниями
