Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему к уроку геометрии в 9 классе на тему Правильные многоугольники

Содержание

МАТЕМАТИКА…выявляет порядок, симметрию и определенность, а это важнейшие виды прекрасного. Аристотель
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ И ИХ СВОЙСТВАУРОК ГЕОМЕТРИИ В 9 КЛАССЕ МАТЕМАТИКА…выявляет порядок, симметрию и определенность, а это важнейшие виды прекрасного. Из историиПравильные многоугольники были известны еще в глубокой древности. В египетских и ОБЩИЕ СВЕДЕНИЯПравильным многоугольником -называется многоугольник , у которого все стороны равны и Снежинки имеют форму правильных многоугольников ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ В ПРИРОДЕ ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ В ПРИРОДЕПравильные многоугольники встречаются в природе. Пример – это ПАРКЕТЫ ИЗ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВПаркеты из одинаковых правильных многоугольников Паркеты из разных правильных многоугольников ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ В ПРИРОДЕМногие простейшиеморские организмы( радиолярии )имеют формуправильныхмногоугольников ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬОкружность, вписанная в правильный многоугольник, касается сторон многоугольника в СВОЙСТВА ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВПравильный многоугольник является выпуклым многоугольникомКаждый угол правильного многоугольника вычисляется по ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ Площадь правильного многоугольникаРадиус описанной окружности Формулы ВыполнитьВ классе № 179, 181, 184, 186, 204Домашнее заданиеИзучить §6, вопросы 1-8,
Слайды презентации

Слайд 2 МАТЕМАТИКА…выявляет порядок, симметрию и определенность, а это важнейшие

МАТЕМАТИКА…выявляет порядок, симметрию и определенность, а это важнейшие виды прекрасного.

виды прекрасного.

Аристотель

Слайд 3 Из истории

Правильные многоугольники были известны еще в глубокой

Из историиПравильные многоугольники были известны еще в глубокой древности. В египетских

древности. В египетских и вавилонских старинных памятниках встречаются правильные

четырехугольники, шестиугольники и восьмиугольники в виде изображений на стенах и украшений, высеченных их камня.
Древнегреческие ученые стали проявлять большой интерес к правильным многоугольникам еще со времен Пифагора.
Учение о правильных многоугольниках было систематизировано и изложено в 4 книге «Начал» Евклида.

Слайд 4 ОБЩИЕ СВЕДЕНИЯ
Правильным многоугольником -называется многоугольник , у которого

ОБЩИЕ СВЕДЕНИЯПравильным многоугольником -называется многоугольник , у которого все стороны равны

все стороны равны и все углы равны.
Примерами правильных многоугольников

являются равносторонний треугольник и квадрат





Слайд 5 Снежинки имеют форму правильных

Снежинки имеют форму правильных многоугольников ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ В ПРИРОДЕ

многоугольников
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ В ПРИРОДЕ

Слайд 6 ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ В ПРИРОДЕ
Правильные многоугольники встречаются в природе.

ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ В ПРИРОДЕПравильные многоугольники встречаются в природе. Пример – это

Пример – это пчелиные соты, которые представляют собой прямоугольник,

покрытый правильными шестиугольниками. На этих шестиугольниках пчелы выращивают из воска ячейки, представляющие собой прямые шестиугольные призмы. В них пчелы и откладывают мед, а затем снова покрывают сплошным прямоугольником из воска

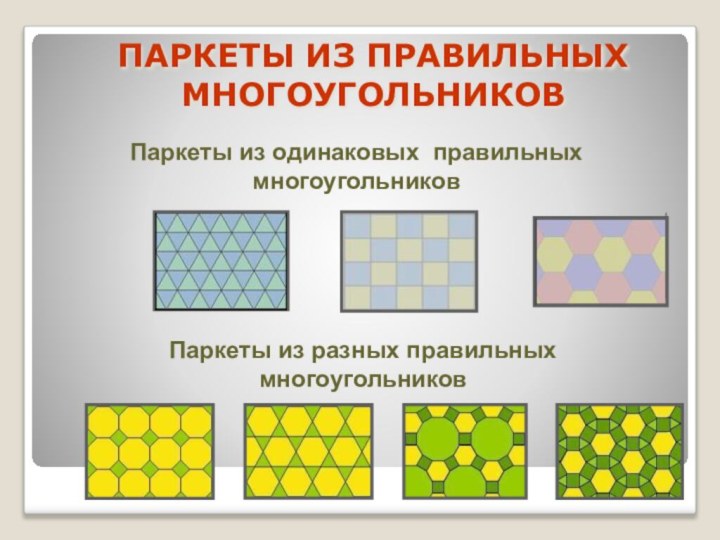
Слайд 7 ПАРКЕТЫ ИЗ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ
Паркеты из одинаковых правильных многоугольников

ПАРКЕТЫ ИЗ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВПаркеты из одинаковых правильных многоугольников Паркеты из разных правильных многоугольников


Паркеты из разных правильных многоугольников

Слайд 8 ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ В ПРИРОДЕ
Многие простейшие
морские организмы
( радиолярии )
имеют

ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ В ПРИРОДЕМногие простейшиеморские организмы( радиолярии )имеют формуправильныхмногоугольников

форму
правильных
многоугольников

Слайд 9 ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ
Окружность, вписанная в правильный многоугольник, касается

ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬОкружность, вписанная в правильный многоугольник, касается сторон многоугольника

сторон многоугольника в их серединах.


Центр окружности, описанной около правильного

многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.

Слайд 10 СВОЙСТВА ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ
Правильный многоугольник является выпуклым многоугольником
Каждый угол

СВОЙСТВА ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВПравильный многоугольник является выпуклым многоугольникомКаждый угол правильного многоугольника вычисляется

правильного многоугольника вычисляется по формуле
Теорема:
Любой правильный многоугольник является

одновременно вписанным в окружность и описанным около окружности, причем центры описанной и вписанной окружностей совпадают

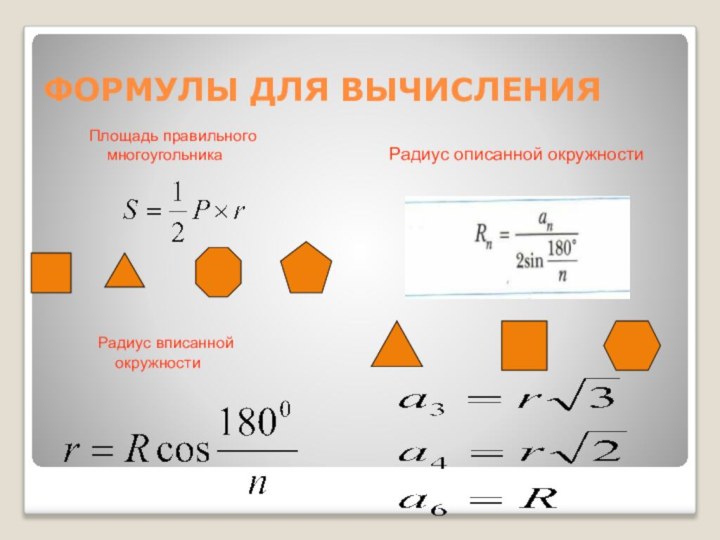
Слайд 11 ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ




Площадь правильного
многоугольника

Радиус описанной

ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ Площадь правильного многоугольникаРадиус описанной окружности Радиус вписанной окружности

окружности

Радиус вписанной

окружности




Слайд 12 Формулы

Формулы
  • Имя файла: prezentatsiya-k-uroku-geometrii-v-9-klasse-na-temu-pravilnye-mnogougolniki.pptx
  • Количество просмотров: 147
  • Количество скачиваний: 1
- Предыдущая Презентация по технологии на тему Бюджет семьи. Рациональное планирование расходов (8 класс)
Следующая - Работа с семьями, находящимися в социально опасном положении, а также с их детьми

Похожие презентации

Презентация по геометрии на тему Симметрия 8 класс Презентация по геометрии на тему Симметрия 8 класс 150
Измерительные работы на местности. Геометрия 8класс. Измерительные работы на местности. Геометрия 8класс. 274
Учебный проект о квадрате и его применении в жизни. Учебный проект о квадрате и его применении в жизни. 204
Треугольники 5 класс Треугольники 5 класс 188
Звездный час Звездный час 160
Вписанная окружность. Описанный многоугольник Вписанная окружность. Описанный многоугольник 166
Презентация по математике Справочное пособие по геометрии (7 класс) Презентация по математике Справочное пособие по геометрии (7 класс) 165
Презентация по теме Движение Презентация по теме Движение 166
Объём пирамиды Объём пирамиды 162
Презентация по геометрии на тему Цилиндр Презентация по геометрии на тему Цилиндр 137
Презентация к уроку по геометрии в 7 классе Треугольники Презентация к уроку по геометрии в 7 классе Треугольники 168
Методическая разработка по теме Определение параллелограмма. Свойства параллелограмма Методическая разработка по теме Определение параллелограмма. Свойства параллелограмма 175
Пифагор и его теорема Пифагор и его теорема 187
Преобразование плоскости Преобразование плоскости 194
Презентация по геометрии по теме Инверсия Презентация по геометрии по теме Инверсия 233
Медиана биссектриса и высота треугольника Медиана биссектриса и высота треугольника 151
Презентация по геометрии на тему Теоремы Чевы и Менелая Презентация по геометрии на тему Теоремы Чевы и Менелая 160
Классификация геометрических объектов Классификация геометрических объектов 178
Презентация к уроку математике 8 класс Площадь параллелограмма Презентация к уроку математике 8 класс Площадь параллелограмма 195
Презентация по геометрии Теорема Пифагора Презентация по геометрии Теорема Пифагора 163
Три признака равенства треугольников Три признака равенства треугольников 136
Задачи на построение Задачи на построение 158
Точка, прямая, отрезок, луч и угол Точка, прямая, отрезок, луч и угол 154
Геометрические фигуры в графике Геометрические фигуры в графике 156
Иран Иран 162
Презентация по геометрии по теме Пирамида, правильная пирамида, усеченная пирамида. Презентация по геометрии по теме Пирамида, правильная пирамида, усеченная пирамида. 175
Геометричиские преобразования в пространстве Геометричиские преобразования в пространстве 158
Как найти скалярное произведение векторов Как найти скалярное произведение векторов 148
Открытый урок по геометрии в 7 классе по теме Сумма углов треугольника Открытый урок по геометрии в 7 классе по теме Сумма углов треугольника 74
Решение треугольников 9 класс Решение треугольников 9 класс 214