Презентация на тему по геометрии на тему Тетраэдр и параллелепипед (10 класс)

Содержание

2. Тетраэдр – простейший многогранник, гранями которого являются
3. Элементы тетраэдраГраниОснованиеРебраВершины
4. Тетраэдр в жизни человека
6. ПараллелепипедПараллелепипед – многогранник, у которого шесть граней и
7. Параллелепипед в жизни человека
8. Элементы параллелепипедаРебраОснованияВершиныБоковые грани
9. Параллелепипед ABCDA1B1C1D1АBD1A 1B 1DCC 1Две грани параллелепипеда,
10. Свойства параллелепипеда1. Противоположные грани параллелепипеда параллельны и равны.С1А1D1АСВDВ1
11. Свойства параллелепипеда1. Противоположные грани параллелепипеда параллельны и равны.С1А1D1АСВDВ1
12. В1А1АDСВD1С1
13. 2. Диагонали параллелепипеда пересекаются в одной точке
14. Скачать презентацию
15. Похожие презентации

Тетраэдр – простейший многогранник, гранями которого являются четыре треугольника. У тетраэдра 4 грани, 4 вершины и 6 рёбер. Тетраэдр, у которого все грани — равносторонние треугольники, называется правильным. Правильный тетраэдр является одним из пяти правильных многогранников.

Главная
Геометрия
Презентация по геометрии на тему Тетраэдр и параллелепипед (10 класс)

Тетраэдр и параллелепипедГБОУ Гимназия №5 Лихолетов Георгий 10А Учитель: Мотуз Т.В.г. Севастополь

Тетраэдр – простейший многогранник, гранями которого являются четыре треугольника. У тетраэдра 4

Элементы тетраэдраГраниОснованиеРебраВершины

Презентация по геометрии на тему Тетраэдр и параллелепипед (10 класс)

ПараллелепипедПараллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.Прямоугольный параллелепипед – это параллелепипед,

Элементы параллелепипедаРебраОснованияВершиныБоковые грани

Параллелепипед ABCDA1B1C1D1АBD1A 1B 1DCC 1Две грани параллелепипеда, имеющие общее ребро, называются смежными,

Свойства параллелепипеда1. Противоположные грани параллелепипеда параллельны и равны.С1А1D1АСВDВ1

2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.Рассмотрим

Слайды презентации

Слайд 2 Тетраэдр – простейший многогранник, гранями которого являются четыре

Тетраэдр – простейший многогранник, гранями которого являются четыре треугольника. У тетраэдра

треугольника. У тетраэдра 4 грани, 4 вершины и 6

рёбер. Тетраэдр, у которого все грани — равносторонние треугольники, называется правильным. Правильный тетраэдр является одним из пяти правильных многогранников.

Слайд 3 Элементы тетраэдра
Грани
Основание
Ребра
Вершины

Слайд 4 Тетраэдр в жизни человека

Слайд 5

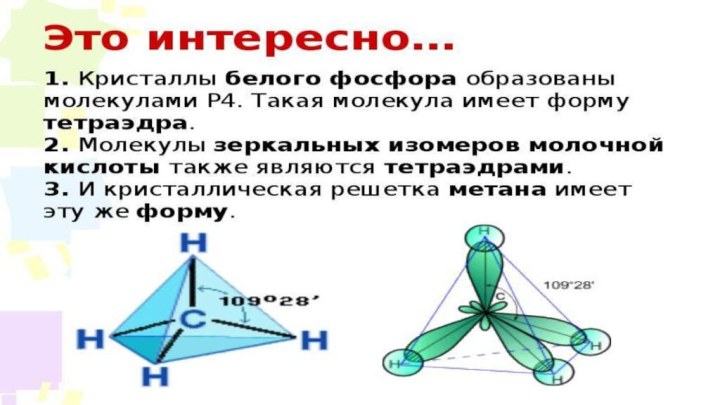
Слайд 6 Параллелепипед
Параллелепипед – многогранник, у которого шесть граней и каждая

ПараллелепипедПараллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.Прямоугольный параллелепипед –

из них параллелограмм.
Прямоугольный параллелепипед – это параллелепипед, у которого все грани прямоугольники.

Слайд 7 Параллелепипед в жизни человека

Слайд 8 Элементы параллелепипеда
Ребра
Основания
Вершины
Боковые грани

Слайд 9 Параллелепипед ABCDA1B1C1D1
А
B
D1
A 1
B 1
D
C
C 1
Две грани параллелепипеда, имеющие

Параллелепипед ABCDA1B1C1D1АBD1A 1B 1DCC 1Две грани параллелепипеда, имеющие общее ребро, называются

общее ребро, называются смежными, а не имеющие общих рёбер

– противоположными.
Две вершины, не принадлежащие одной грани называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. В каждом параллелепипеде 4 диагонали.

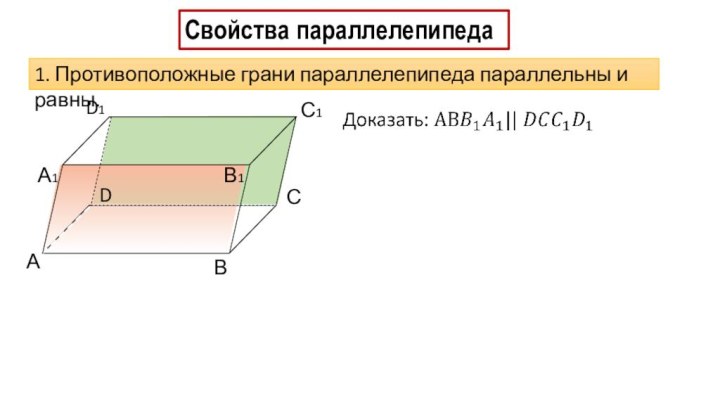
Слайд 10 Свойства параллелепипеда
1. Противоположные грани параллелепипеда параллельны и равны.
С1
А1
D1
А
С
В
D
В1

Слайд 11 Свойства параллелепипеда
1. Противоположные грани параллелепипеда параллельны и равны.
С1
А1
D1
А
С
В
D
В1

Слайд 12 В1
А1
А
D
С
В
D1
С1

Слайд 13 2. Диагонали параллелепипеда пересекаются в одной точке и

2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой

делятся этой точкой пополам.
Рассмотрим четырёхугольник A1D1CB, диагонали которого A1C

и D1B являются диагоналями параллелепипеда ABCDA1B1C1D1. Т.к. A1D1 II BC и A1D1=BC, то A1D1CB - параллелограмм. Поэтому диагонали A1C и D1B пересекаются в некоторой точке О и этой точкой делятся пополам.