- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему исследовательской работы учащейся 10 класса МОУ икейская СОШ Рябовой Екатерины В мире многогранников
Содержание
- 2. Цель проекта: Показать значимость многогранников в нашей
- 3. Пифагор (Евфорб, Эфалид, Гермотим, Пирр) родился на острове Самос приблизительно в 580 году до нашей эры
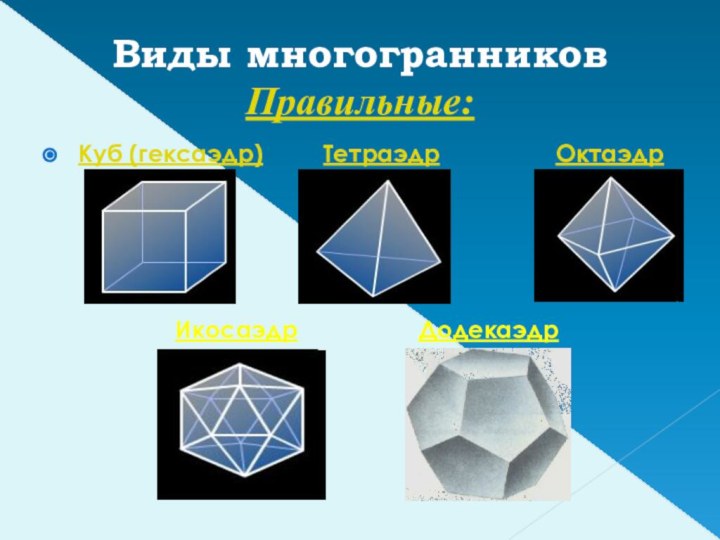
- 4. Виды многогранников Правильные:Куб (гексаэдр)
- 5. Виды многогранников Полуправильные : Кубооктаэдр Икосододекаэдр
- 6. Ромбокубооктаэдр
- 7. Икосаэдр
- 8. Пространственная фигура, состоящая из 7 кубов
- 9. Композиция из многогранников
- 10. Правильные звездчатые многогранники (некоторые виды икосаэдров)
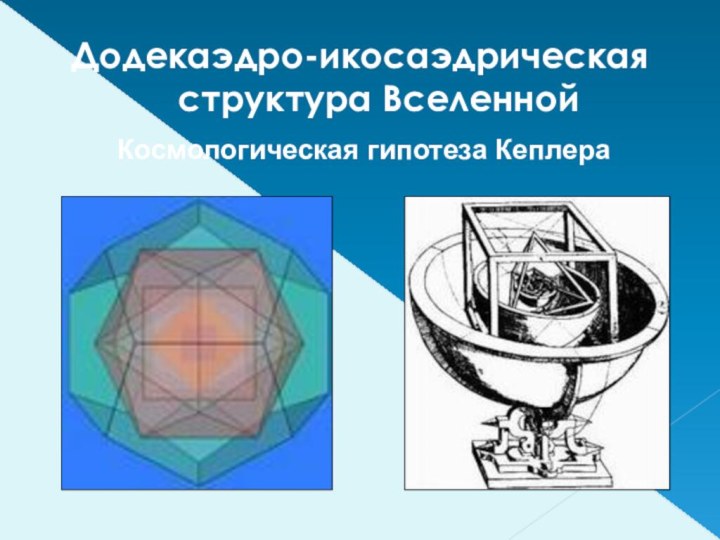
- 11. Додекаэдро-икосаэдрическая структура ВселеннойКосмологическая гипотеза Кеплера
- 12. Додекаэдро-икосаэдрическая структура ВселеннойПлатон писал: "Земля, если взглянуть
- 13. Додекаэдро-икосаэдрическая структура ВселеннойПлатоновы тела Платон рассматривал четыре
- 14. Додекаэдро-икосаэдрическая структура Вселенной
- 15. Додекаэдро-икосаэдрическая структура Вселенной
- 16. Додекаэдро-икосаэдрическая структура Вселенной
- 17. Додекаэдро-икосаэдрическая структура Вселенной
- 18. Додекаэдро-икосаэдрическая структура ВселеннойВселенная
- 19. Многогранники в природеСимметрия многогранников в биологии«Мой дом
- 20. Многогранники в химииКристаллы поваренной соли (NaCl) имеют форму куба
- 21. Многогранники в природе (кристаллы)Алмаз (октаэдр)Шеелит (пирамида)Хрусталь (призма)Поваренная соль (куб)
- 22. Многогранники в изобразительном искусстве
- 23. Ма́уриц Корне́лис Э́шер (17 июня 1898 — 27
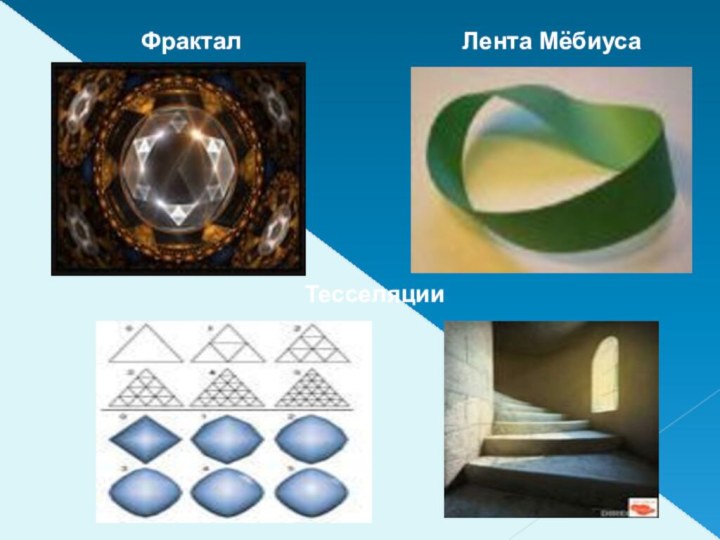
- 25. Фрактал Тесселяции Лента Мёбиуса
- 26. Леонардо да Винчи
- 28. Невозможные фигурыIstvan Orosz "Перекрестки" (1999). Репродукция гравюры по металлу.
- 29. Невозможные фигурыБливетАрка в стиле «бливет»
- 30. Невозможные фигурыКак устроен "Бливет".
- 31. Невозможные фигурыУкрупненный фрагмент картины с невозможным кубиком.
- 32. Многогранники в архитектуре
- 33. Заключение Жизнь человека
- 34. Скачать презентацию
- 35. Похожие презентации
Цель проекта: Показать значимость многогранников в нашей жизни, их неоспоримое многообразие, красоту и изящество. Основной метод, используемый в работе - метод систематизации и обработки информации.































Слайд 2
Цель проекта:
Показать значимость многогранников в нашей жизни,
их неоспоримое многообразие, красоту и изящество.
в работе - метод систематизации и обработки информации.Слайд 3 Пифагор (Евфорб, Эфалид, Гермотим, Пирр) родился на острове
Самос приблизительно в 580 году до нашей эры
Слайд 5
Виды многогранников Полуправильные :
Кубооктаэдр
Икосододекаэдр
Усеченный тетраэдр
Усечённый куб
Усечённый октаэдр
Усечённый додекаэдр
Усечённый икосаэдр
Ромбокубооктаэдр
Ромбоусечённый кубоктаэдр
Ромбоикосододекаэдр
Ромбоусечённый икосододекаэдр
Курносый куб
Курносый додекаэдр
Архимедовы тела
Слайд 12
Додекаэдро-икосаэдрическая структура Вселенной
Платон писал: "Земля, если взглянуть на
нее сверху, похожа на мяч, сшитый из 12 кусков
кожи".(427-347гг. до н.э.)
Платон родился в 427г. до н.э.
в Афинах.
Слайд 13
Додекаэдро-икосаэдрическая структура Вселенной
Платоновы тела
Платон рассматривал четыре стихии
(земля, воздух, вода, огонь) как совокупность мельчайших невидимых частиц,
имеющих формы правильных многогранников. Так частицы огня есть тетраэдры, воздуха - октаэдры, воды- икосаэдры, земли - кубы. Однако позднее он вводит пятый элемент стихии - эфир, частицам которого придается форма додекаэдра.
Слайд 19
Многогранники в природе
Симметрия многогранников в биологии
«Мой дом построен
по законам самой строгой
архитектуры познавая геометрию сот». (
Евклид) Скелет одноклеточного организма
феодарии (Circjgjnia icosahtdra)
по форме напоминает икосаэдр.
Слайд 21
Многогранники в природе (кристаллы)
Алмаз (октаэдр)
Шеелит (пирамида)
Хрусталь (призма)
Поваренная соль
(куб)
Слайд 23
Ма́уриц Корне́лис Э́шер (17 июня 1898 —
27 марта
1972) — нидерландский художник-график. Известен прежде всего своими концептуальными литографиями,
гравюрами на дереве и металле, в которых он мастерски исследовал пластические аспекты понятий бесконечности и симметрии, а также особенности психологического восприятия сложных трёхмерных объектов.Слайд 26 Леонардо да Винчи (Leonardo
da Vinci) (1452-1519) известен своими достижениями в качестве изобретателя
и художника.В его записных книгах содержатся первые из известных примеров анаморфного искусства, использующего искаженные сетки перспективы.
Его наклонные анаморфные изображения представляют объекты, которые должны рассматриваться под углом, чтобы они выглядели неискаженными.