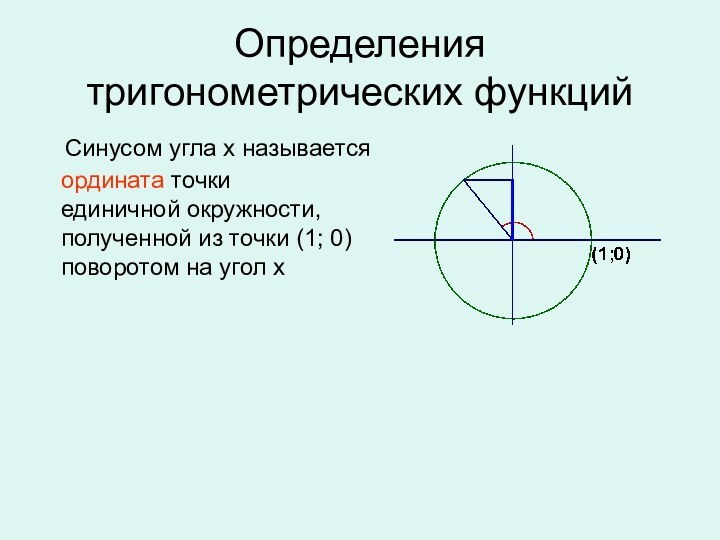
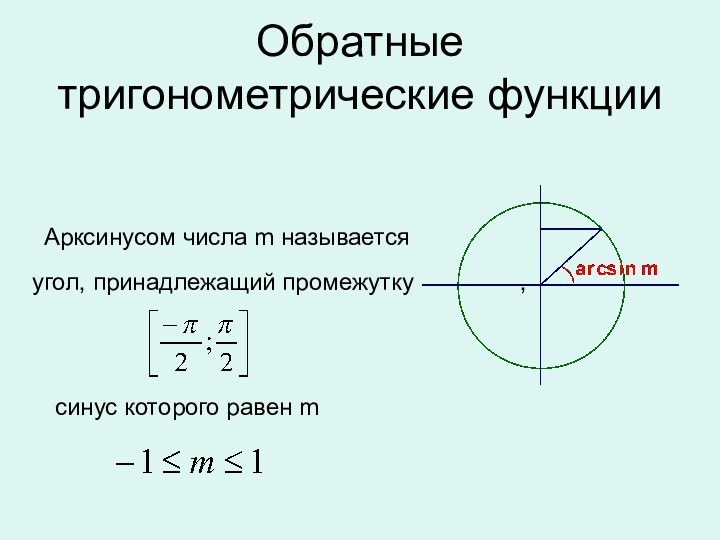
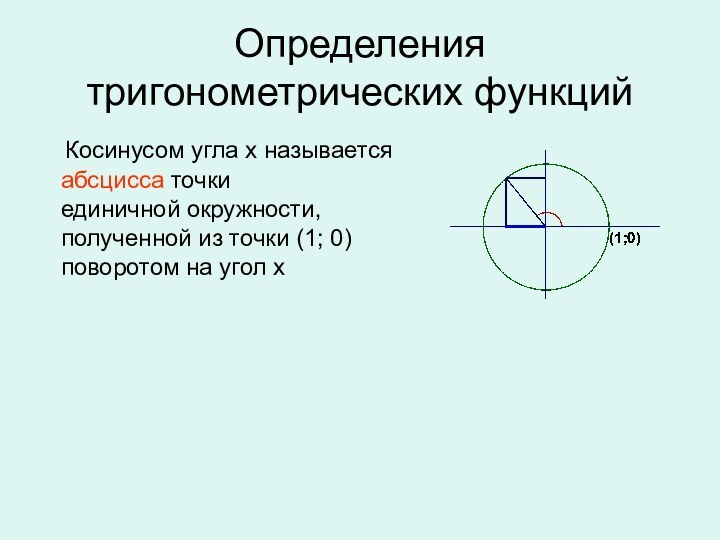
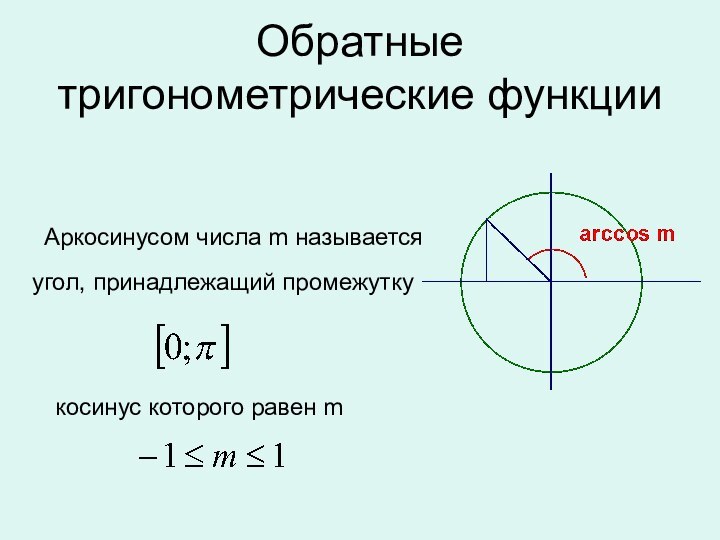
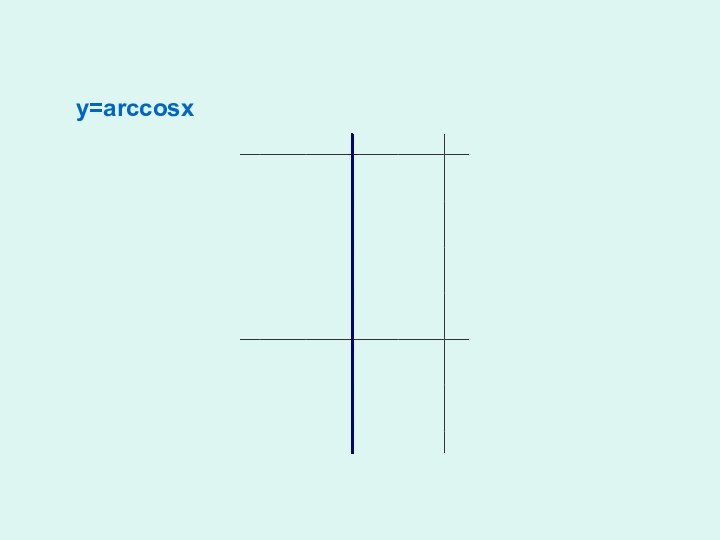
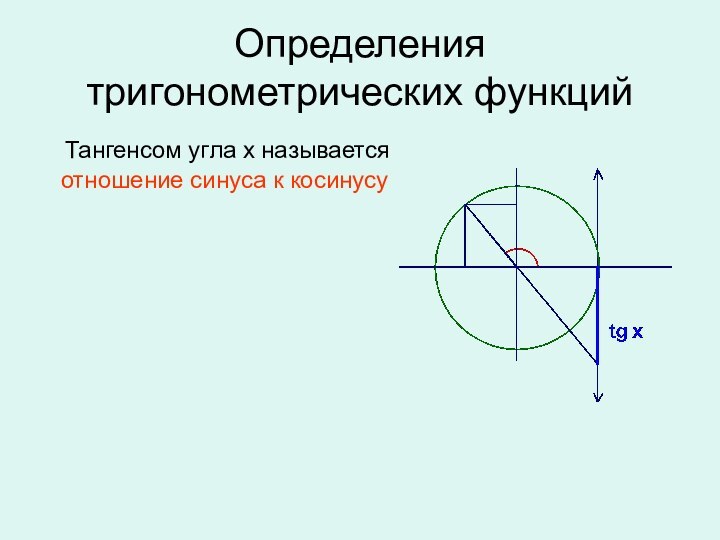
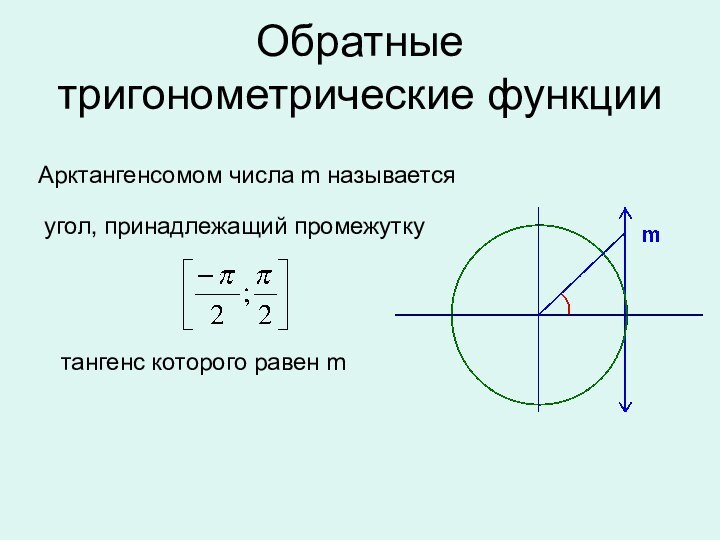
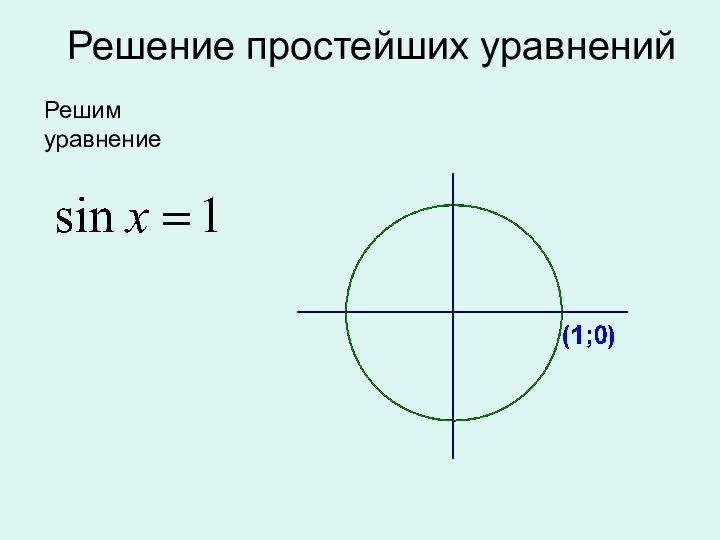
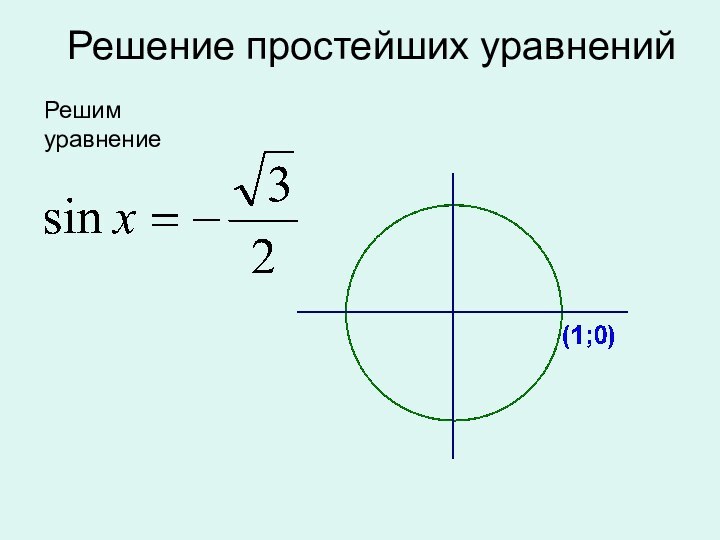
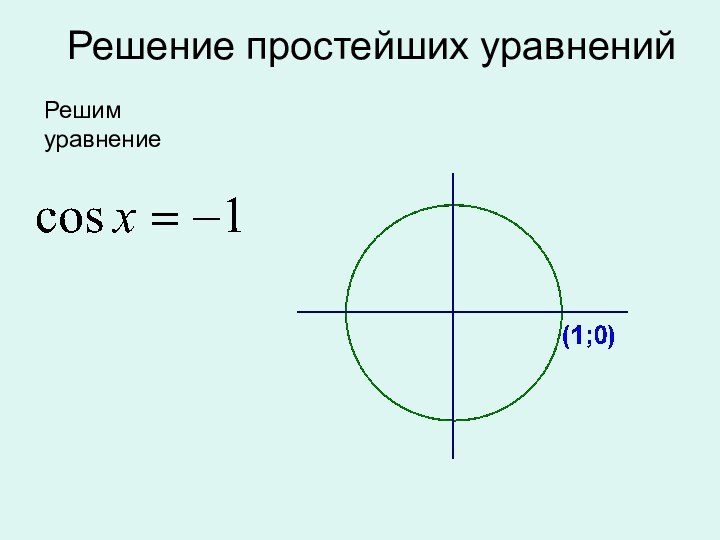
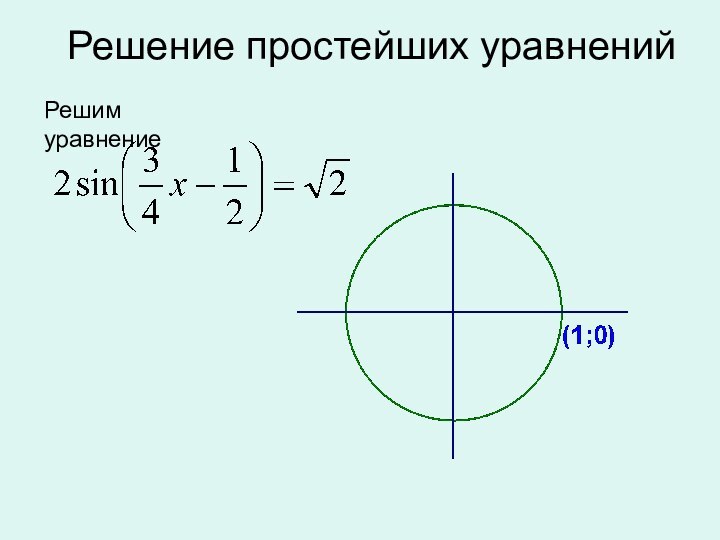
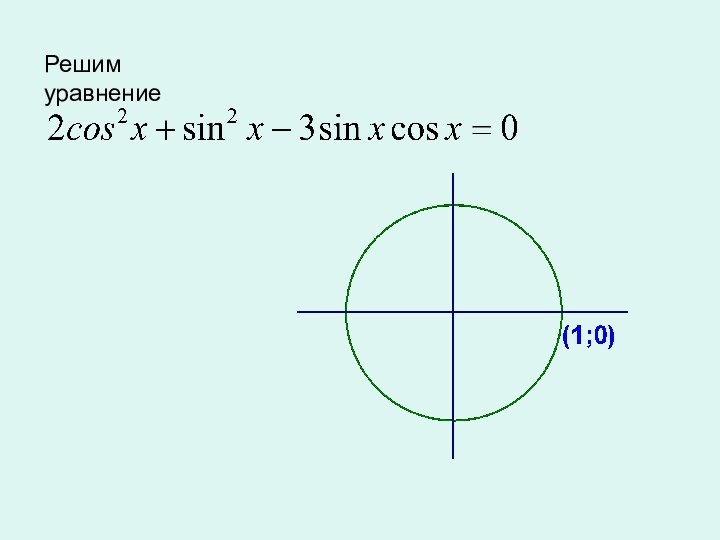
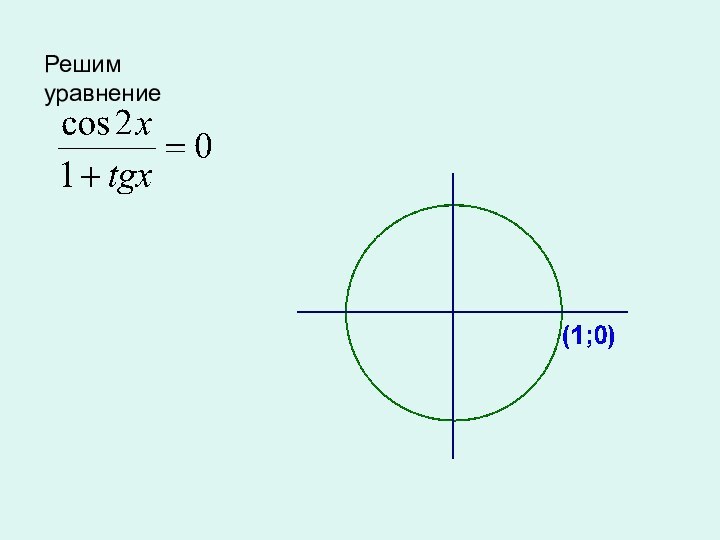
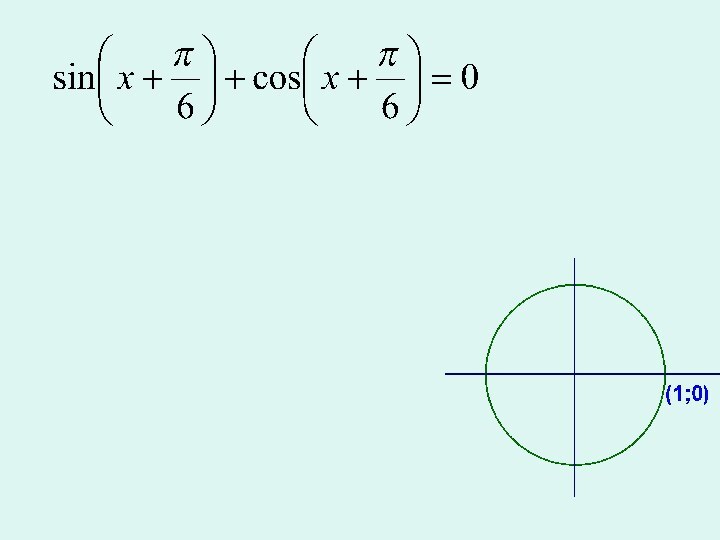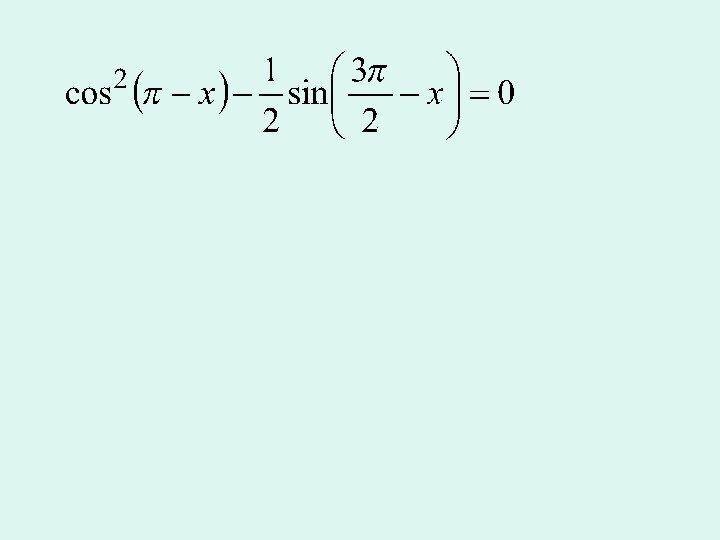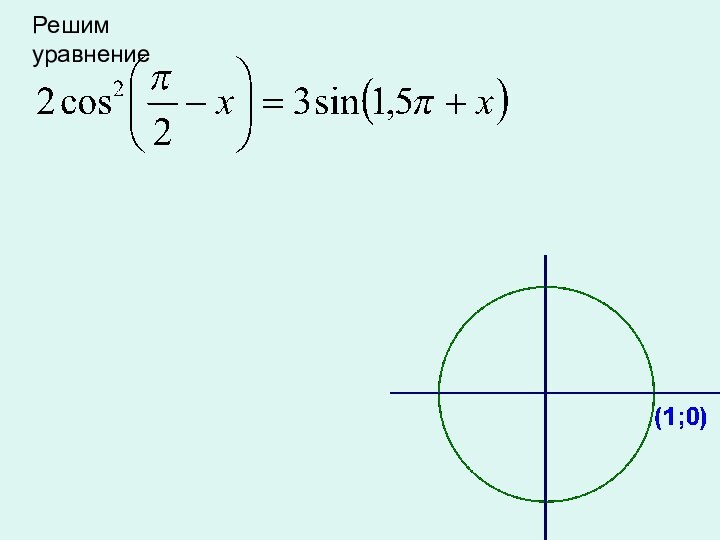окружности,
полученной из точки (1; 0)
поворотом на угол
х
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть