- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Взаимное расположение прямых в пространстве
Содержание
- 2. – прямые скрещивающиеся;– прямые пересекаются;– прямые параллельные;–
- 3. Две прямые в пространстве называются
- 5. Прямые, которые имеют общую точку и лежат в одной плоскости, называются пересекающимися.Пересекающиеся прямые
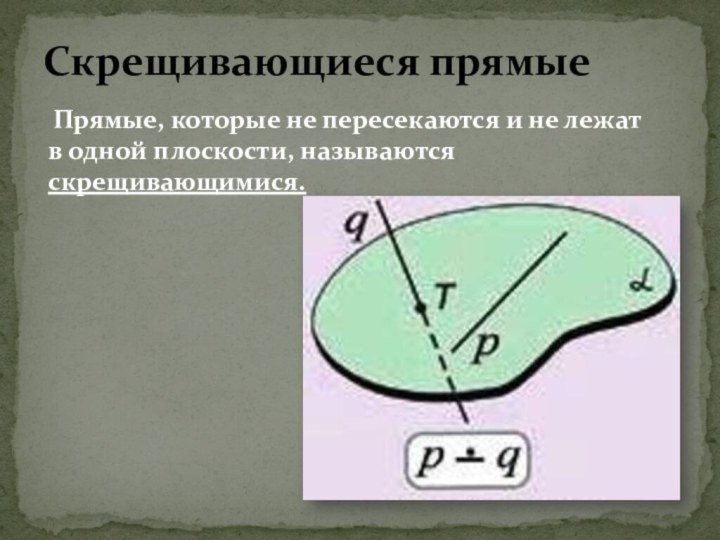
- 7. Прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися.Скрещивающиеся прямые
- 15. Через точку, не лежащую на
- 16. Две прямые, параллельные третьей прямой,
- 18. 1) точки, которые принадлежат плоскости грани АВС;2)
- 19. Известно, что точки А,В,С,D лежат
- 20. Известно, что точки А,В,С,D не
- 21. Треугольник ВКС и прямоугольник АВСD
- 22. Квадрат АВСD и трапеция BEFC
- 23. Точки K,L,M,N – середины ребер
- 24. Назовите случаи взаимного расположения прямых в пространстве.О
- 25. Скачать презентацию
- 26. Похожие презентации
– прямые скрещивающиеся;– прямые пересекаются;– прямые параллельные;– прямые совпадают.Возможны четыре различных случая расположения двух прямых в пространстве:
























Слайд 3 Две прямые в пространстве называются параллельными,
если они лежат в одной плоскости и не пересекаются.
Параллельные
прямыеСлайд 5 Прямые, которые имеют общую точку и
лежат в одной плоскости, называются пересекающимися.
Пересекающиеся прямые
Слайд 7 Прямые, которые не пересекаются и не
лежат в одной плоскости, называются скрещивающимися.
Скрещивающиеся прямые
Слайд 15 Через точку, не лежащую на данной
прямой, можно провести прямую, параллельную этой прямой, притом только
одну.Дано: а, А а.
Доказать: b a, b - единственная
Доказательство.
1. Через прямую а и точку А проведём
плоскость .
2. Через точку А проведём b a.
3. Докажем, что b – единственная.
Допустим, что существует b1 а. Через а и b1 можно провести 1. 1 должна проходить через А и а. Но такая плоскость единственная, значит, совпадает с 1, b совпадает с b1.
ТЕОРЕМА :
Слайд 16
Две прямые, параллельные третьей прямой, параллельны.
а
а, b, с – лежат в одной плоскости.b с Пусть b и с не параллельны.
Тогда они пересекаются в точке,
через которую будут проходить
две прямые параллельные а, что
противоречит аксиоме 1.
Значит, b c.
Теорема:
ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ
Слайд 17
а, b, с – не лежат в одной плоскости.
Тогда через а и с проведем
плоскость , а через с и b –
плоскость ( по определению
параллельных прямых).
и - различны.
Поставим на прямой b точку В. Через В и с проведём плоскость . Она пересечет по прямой b1.
Так как в через В уже проходит b с, то b1 не с.
То есть b1 с = К, К, К. Однако К b1 значит К.
Точка К принадлежит одновременно всем трем плоскостям. Но точки общие для и лежат на прямой а. Поэтому а проходит через К, что противоречит условию а с.
Итак, b1 не с, b1 с. Но в b с.
Значит, b1 и b совпадают. а b.
Слайд 18
1) точки, которые принадлежат плоскости грани АВС;
2) точки
которые не лежат в плоскости грани АВС;
3) общие точки
плоскостей граней АВС и АВS;4) прямую пересечения плоскостей граней АВС и SBC;
5) плоскость, которая проходит через прямые АВ и ВС;
6) плоскость, которая не содержит прямых АВ и ВС.
Задание: Пользуясь изображением, запишите:
Слайд 19 Известно, что точки А,В,С,D лежат в
одной плоскости.
Определите, могут ли прямые АВ и
СD:а) быть параллельными;
б) пересекаться;
в) быть скрещивающимися.
Задача № 1
Слайд 20 Известно, что точки А,В,С,D не лежат
в одной плоскости.
Определите, могут ли прямые
АВ и СD:а) быть параллельными;
б) пересекаться;
в) быть скрещивающимися.
Задача № 2
Слайд 21 Треугольник ВКС и прямоугольник АВСD не
лежат в одной плоскости. Точки М и N –
середины отрезков ВК и КС соответственно. Докажите, что АD МN.Найдите АD, если МN = 4 см.
Задача № 3
Слайд 22 Квадрат АВСD и трапеция BEFC (
ВС и EF – основания) не лежат в одной
плоскости. Точки M и N – середины отрезков BE и FC соответственно. Докажите, что MN АD. Найдите MN, если АВ = 8 см, EF = 4 см.Задача № 4
Слайд 23 Точки K,L,M,N – середины ребер AB,
AC, CD, DB тетраэдра, все ребра которого равны.
Найдите длину ребра тетраэдра, если периметр, образованного четырехугольника KLMN равен 4a.Задача № 5
Слайд 24
Назовите случаи взаимного расположения прямых в пространстве.
О каком
взаимном расположении прямых в пространстве Вы сегодня узнали впервые?
Дать определение.
Назовите случаи взаимного расположения прямых в пространстве на примере классной комнаты.
Вопросы: