Слайд 2
Объект исследования - раздел математики - геометрия.
Предмет исследования
– многогранники.
Проблема:
действительно ли многогранники уникальны и находятся вокруг
нас?
Гипотеза:
сможем ли мы моделировать многогранники на практике, находить в окружающем мире, зная историю изучения многогранников, их классификацию.
Слайд 3
Цель: расширить свой кругозор в изучении разновидностей многогранников,
областях их применения.
Задачи:
1.Изучить необходимую литературу, Интернет-ресурсы;
2. Узнать об истории
многогранников;
3.Уточнить признаки классификации многогранников;
4. Уметь моделировать многогранники.
Слайд 4
Геометрия - наука, изучающая формы, размеры
и взаимное расположение геометрических фигур. Она возникла и развивалась
в связи с потребностями практической деятельности человека.
Начало геометрии было положено в древности при решении чисто практических задач. Со временем, когда накопилось большое количество геометрических фактов, у людей появилось потребность обобщения, уяснения зависимости одних элементов от других, установления логических связей и доказательств. Постепенно создавалась геометрическая наука.
Введение.
Слайд 5
Геометрические знания были изложены еще 2200 лет
назад в “Началах” Евклида. Известно, что Евклид
в своей работе опирался на труды десятков предшественников, среди которых были Фалес и Пифагор, Демокрит и Гиппократ.
В своей книге Евклид дал полное математическое описание правильных многогранников. Он описывал структуру тетраэдра, октаэдра, куба, икосаэдра, додекаэдра в данном порядке…
Введение.
Слайд 6
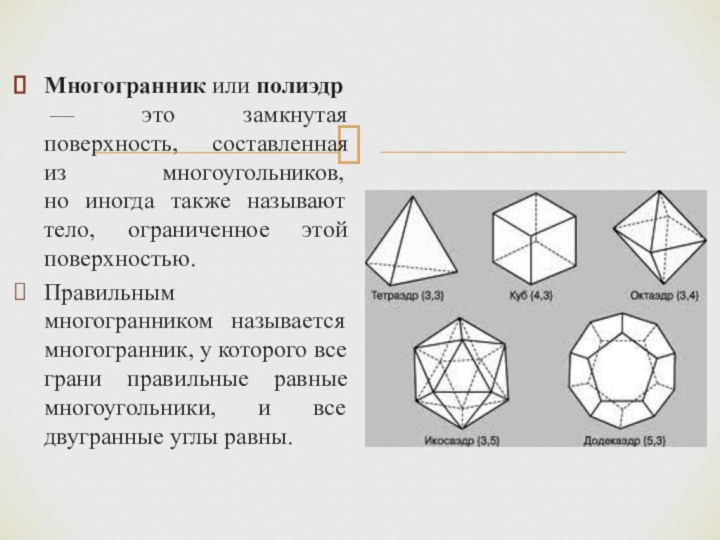
Многогранник или полиэдр — это замкнутая поверхность, составленная из многоугольников,
но иногда также называют тело, ограниченное этой поверхностью.
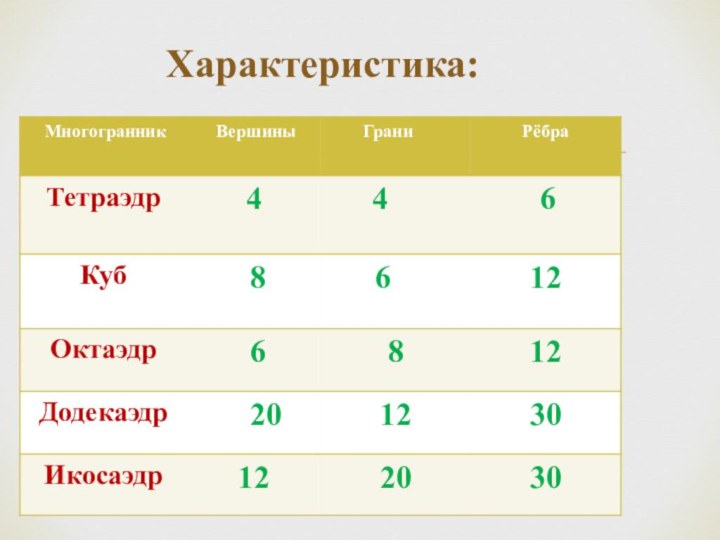
Правильным многогранником называется многогранник, у которого все грани правильные равные многоугольники, и все двугранные углы равны.
Слайд 7
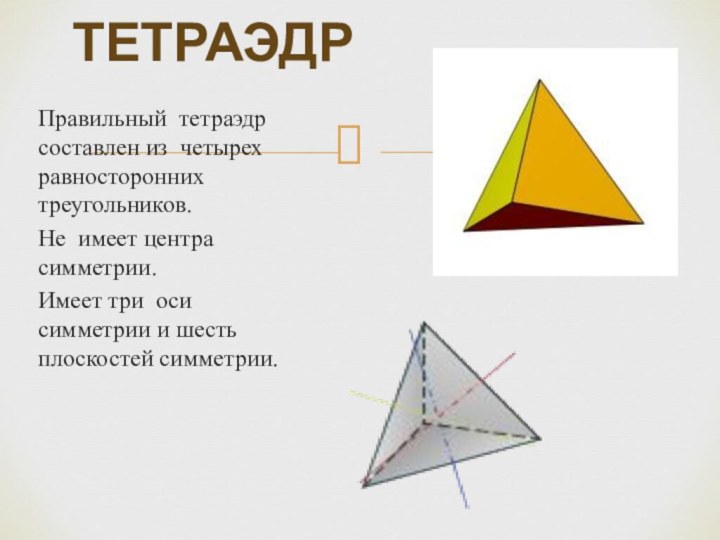
ТЕТРАЭДР
Правильный тетраэдр составлен из четырех равносторонних треугольников.
Не
имеет центра симметрии.
Имеет три оси симметрии и шесть плоскостей
симметрии.
Слайд 8
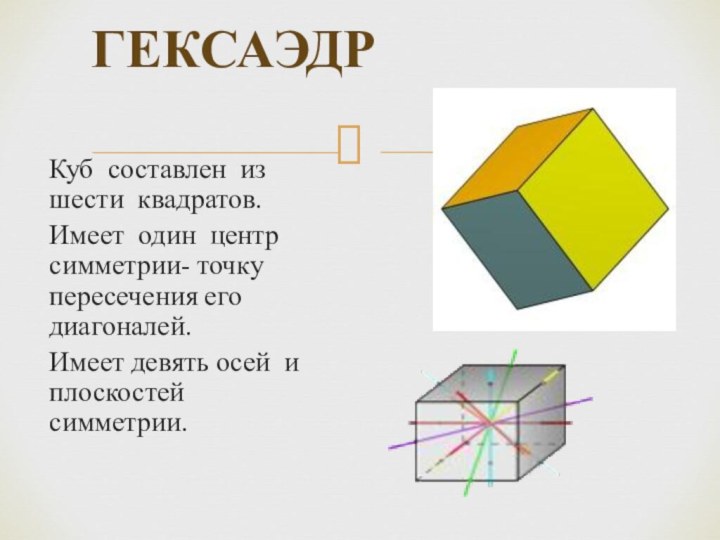
ГЕКСАЭДР
Куб составлен из шести квадратов.
Имеет один центр симметрии-
точку пересечения его диагоналей.
Имеет девять осей и плоскостей симметрии.
Слайд 9
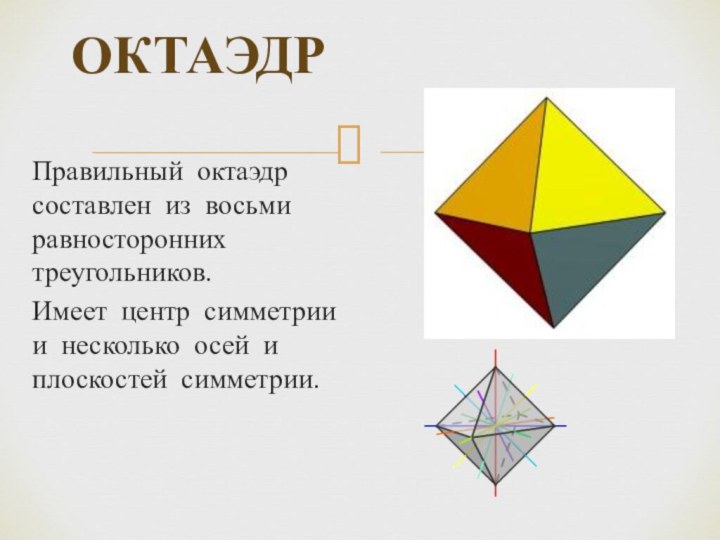
ОКТАЭДР
Правильный октаэдр составлен из восьми равносторонних треугольников.
Имеет
центр симметрии и несколько осей и плоскостей симметрии.
Слайд 10
ДОДЕКАЭДР
Правильный додекаэдр составлен из двенадцати правильных пятиугольников.
Имеет
центр симметрии и несколько осей и плоскостей симметрии.
Слайд 11
ИКОСАЭДР
Правильный икосаэдр составлен из двенадцати равносторонних треугольников.
Имеет центр
симметрии и несколько осей и плоскостей симметрии.
Слайд 12
Платоновые тела
Правильные многогранники называют Платоновыми телами, поскольку
они занимают видное место в философской картине мира, разработанной
великим мыслителем Древней Греции Платоном.
Слайд 14
Правильные многогранники – самые выгодные фигуры, поэтому они
широко распространены в природе.
Подтверждением тому служит форма некоторых кристаллов.
Например, кристаллы поваренной соли имеют форму куба.
скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по форме напоминает икосаэдр.
Пчелиные соты представляют собой пространственный паркет и заполняют пространство так, что не остается просветов
Многогранники в природе
Алмаз(октаэдр)
Шеелит (пирамида)
Хрусталь ( призма)
Поваренная соль (куб)
Слайд 15
Многогранники в живописи
Знаменитый художник, увлекавшийся геометрией Альбрехт
Дюрер(1471- 1528), в известной гравюре «Меланхолия» на переднем плане
изобразил додекаэдр.
Слайд 16
Многогранники в архитектуре
Примером применения в архитектуре Платоновых
тел может служить Великая пирамида в Гизе.
Великая пирамида
была построена как гробница Хуфу, известного грекам как Хеопс. Он был одним из фараонов, или царей древнего Египта, а его гробница была завершена в 2580 году до н.э. Позднее в Гизе было построено еще две пирамиды, для сына и внука Хуфу, а также меньшие по размерам пирамиды для их цариц. Она имеет форму правильного тетраэдра и является древнейшим из Семи чудес древности.
Слайд 17
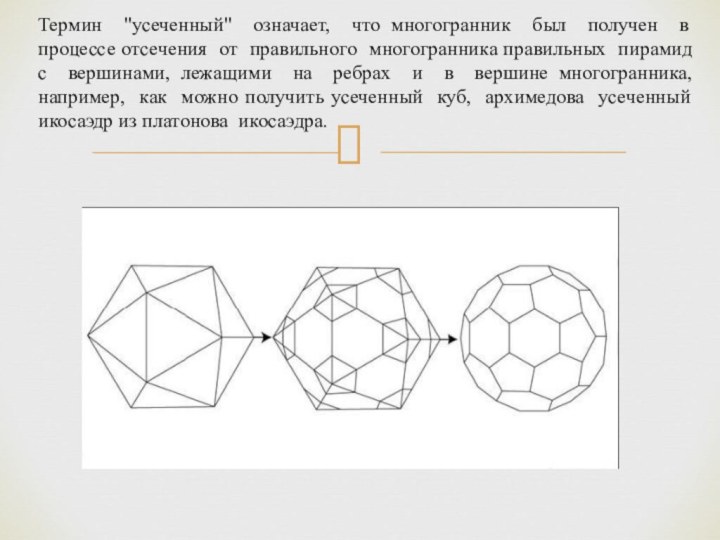
Термин "усеченный" означает, что многогранник был получен в
процессе отсечения от правильного многогранника правильных пирамид с вершинами,
лежащими на ребрах и в вершине многогранника, например, как можно получить усеченный куб, архимедова усеченный икосаэдр из платонова икосаэдра.
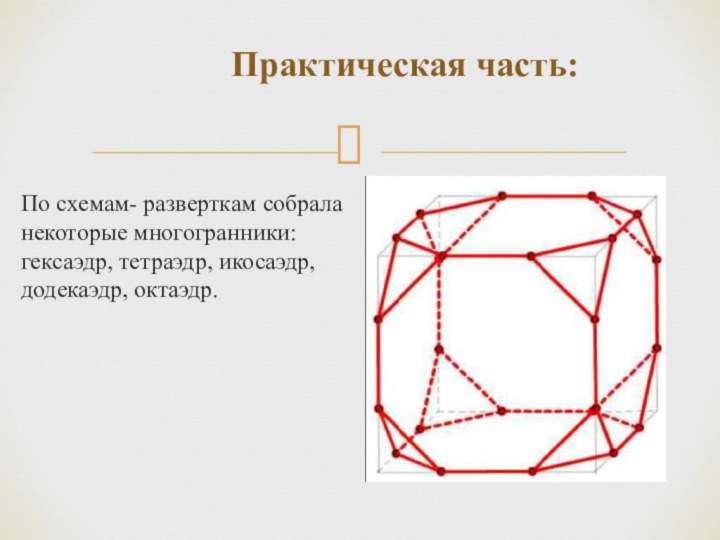
Практическая часть:
По схемам- разверткам собрала некоторые многогранники:
гексаэдр, тетраэдр, икосаэдр, додекаэдр, октаэдр.
Слайд 19
Проделанная исследовательская работа помогла мне узнать и
убедиться в том, что
многогранники на протяжении всей истории человечества
не переставали восхищать нас симметрией, мудростью и совершенством своих форм.
Я провела исследование и сделала вывод:
многогранные формы окружают нас в повседневной жизни повсюду: спичечный коробок, книга, комната, молочные пакеты в форме тетраэдра или параллелепипеда и т.д.
Почти все сооружения, возведённые человеком, от древнеегипетских пирамид до современных небоскрёбов, имеют форму многогранников.
Слайд 20
Я проследила доказательство существования только пяти правильных
многогранников.
Через практическую деятельность собрала по схемам - разверткам несколько
многогранников, попыталась понять, как можно получить усеченные многогранники по чертежам.
Вывод: